
图片来源:百度
原文信息:
Guo, N., Xia, X. and Zhang, J., (2022). A matching model of co-residence with a family network: Empirical evidence from China. The Economic Journal.
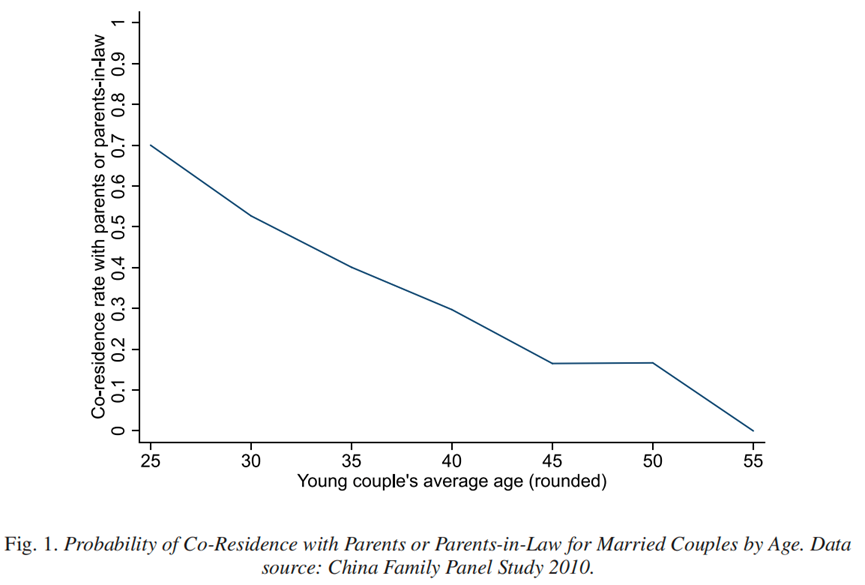
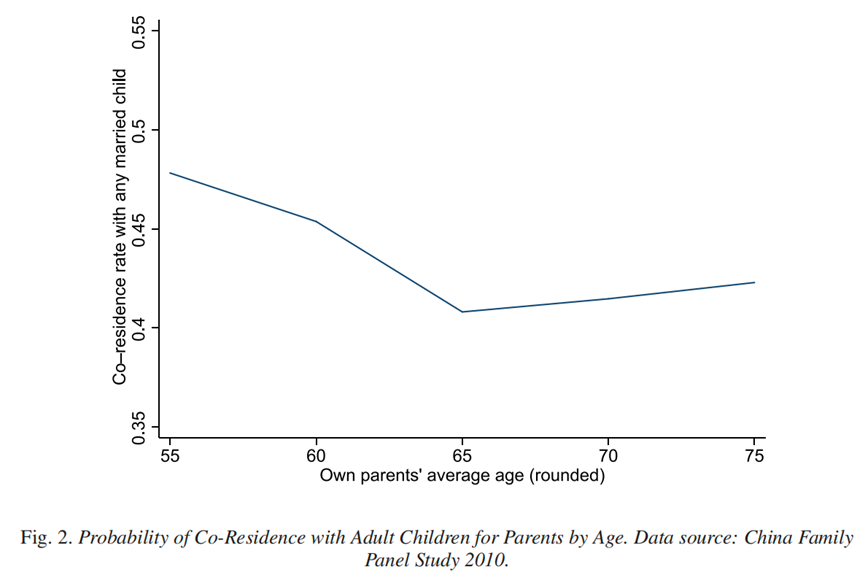
在中国,有相当一部分的已婚子女与其父母或者配偶的父母同住。本文从理论和实证两个方面探究了这一现象背后的原因。具体来说,本文首先构建了一个双边匹配模型来解释这种子女侧和父母侧的同住竞争,然后利用中国的数据对社会规范和经济因素如何影响居住安排进行分析,最后通过反事实实验,检验了房价和计划生育政策对于不同类型的父母和成年子女同住决定的影响。
01
理论模型
本文构建了一个两阶段模型,即认为结婚决策和同住决策是先后发生的。具体来说,在第一阶段,年轻的男性女性进行婚姻匹配,并且会将与父母同住的预期效用作为婚姻剩余的一部分。在第二阶段,子女夫妇基于第一阶段婚姻匹配产生的家庭网络与父母形成共同居住匹配。
在每个阶段,本文将居住安排构建为父母和成年子女之间具有可转移效用(TU)的一对一、双侧匹配模型。其中,一对一匹配是指:在同住匹配中,父母在市场的一边,成年子女在市场的另一边;每个成年子女都可以独自生活,与自己的父母一起生活,或者与配偶父母一起生活;每个父母都可以独自生活,或者最多与自己的一个孩子一起生活。双侧匹配是指:父母和成年子女必须同意这种居住安排;通过假设TU,赞同与成年子女共同居住的父母可以通过提供足够的货币转移从该子女那里“购买”共同居住;同样,成年子女可以通过向父母提供资金转移,在与兄弟姐妹在与父母的共同居住竞争中获胜。
本文使用静态匹配决策,在模型中有两类决策者(父母和成年子女),分别对应两个有限的、不相交的代理集,一个“父”集和一个“成年子”集。一对父母为一个决策单元,称为“父母”,i,一对子女夫妇为决策单位,简称“成年子女”,j。共同居住是一种既能照顾老人(生病)又能照顾孩子(孙辈)的一揽子计划。同时,这也是一个在父母退休、所有成年子女结婚时做出的一次性决定。因此该模型涵盖了整个生命周期中儿童看护和老年护理之间的跨期替代。
此外,该模型有如下假设:所有父母都有N年预期寿命;当父母达到N0岁时,父母和所有成年子女一起做出共同居住的决定;兄弟姐妹不会做出连续的共同居住决定,成年子女结婚的时间也不会影响共同居住决定;父母在N0岁时与成年子女做出同住决定后,不会改变他们的居住安排;人们在每一期都消费掉所有的收入。
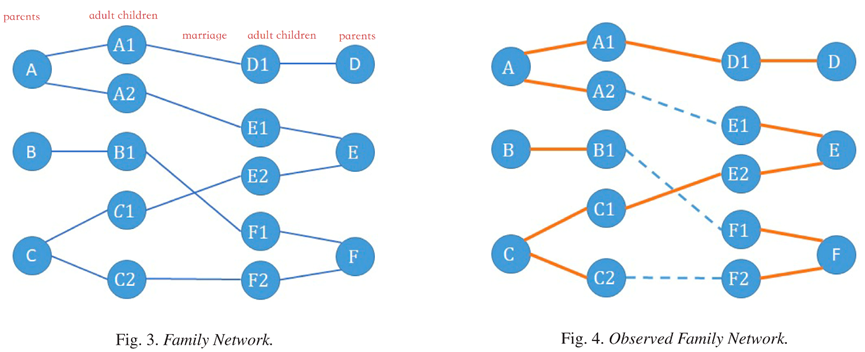
关于模型第二阶段的同住匹配,其取决于预期的共同居住盈余,即为双方共同生居住的效用和单独生活的效用之间的差异。而在一个家庭中,居住安排一方面取决于共同居住盈余,另一方面还取决于家庭网络结构。但是由于数据限制,作者可以观察居住在调查家庭中的成年子女的配偶,但不能观察居住在其他地方的成年子女。因此,本文还对家庭网络结构进行了数据填补。
数据
02
2.1数据来源
本文使用了CFPS2010,CHARLS 2011以及《城市统计年鉴》中的城市经济指标。其中,CFPS使用多阶段概率抽样方法对每个县或社区的家庭进行随机调查,对抽样家庭中所有9岁以上的成员进行访谈。家庭成员被定义为经济上受抚养的直系亲属,或在家庭中连续居住三个月以上并与抽样家庭有经济关系的非直系血亲/婚姻/收养亲属。2010年CFPS包括大约15000个家庭和33600个人。对于每个家庭,CFPS提供人口统计信息和完整的家庭关系图,帮助确定样本中个人的家庭网络中的父母-子女和婚姻关系。
2.2配偶样本构建
CFPS是一项基于家庭的调查,但本文的模型是基于家庭的。基于此,本文首先构建了一个夫妻样本,用于估计婚姻匹配模型。进一步,将夫妇样本扩展到家庭样本,用于估共同居住匹配模型。此外,将夫妻双方的父母年龄限制在55岁至75岁之间;夫妻均为城市本地居民(如果一对夫妇与父母和兄弟姐妹住在同一个城市,他们就被认定为城市本地居民);仅保留已结婚且兄弟姐妹都已结婚的成年子女。最后,样本中共有659对夫妇。
2.3家庭样本构建
家庭样本通过汇集丈夫和妻子所在的家庭构建。家庭被定义为父母双方及其所有子女。在本文样本中,只保留两个家庭中年龄最大的孩子夫妇,以避免重复计算。最终,样本中有1314个家庭。此外,将所有夫妇及其已婚兄弟姐妹合并,形成由3709名已婚个体组成的成年子女样本。
03
模型识别和估计
本文将父母在做出共同居住决定时的年龄N0设置为55岁,预期寿命N设定为75岁。考虑到文化因素的影响,父母和成年子女在同住时的拥挤成本可以随性别和出生顺序而不同。
本文假设父母和子代夫妻的预期收入是教育程度和年龄的函数,同时也考虑了城市固定效应。鉴于本文使用的矩匹配估计仅适用于具有离散值的特性,因此做出以下五个方面的调整:成年子女的受教育程度为1-4,对应初中以下或辍学、初中毕业生、高中毕业生和大学毕业生;成年子女的年龄为1-4,对于34岁以下、34岁至38岁、39岁至43岁以及43岁及以上;兄弟姐妹的数量为1-2,对应于零个或一个兄弟姐妹,以及一个以上的兄弟姐妹;父母受教育程度为1-3,对应小学以下、小学毕业、初中毕业;父母的年龄为1-2,对应65岁以下和65岁以上。每种类型的男性或女性都是这五种特征的组合,总共有192种类型。为了避免过度拟合,本文不是对192种类型中的每一种类型的婚姻盈余进行估计,而是估计参数婚姻盈余函数中的25个参数(如公式(6)所示)。
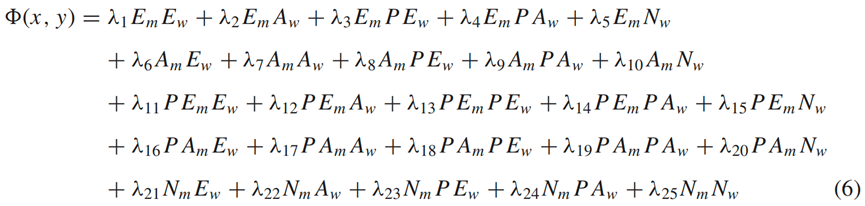
其中,E,A分别为自己的教育程度和年龄。PE,PA分别为父母的教育程度和年龄。N为成年子女兄弟姐妹的数量。下标m, w分别表示男性、女性。
本文通过公式(8)和(9)以及(11)、(12)来分别识别了中父母和成年子女的收入方程中的参数,父母的健康情况以及成年子女夫妇的生育率。具体通过以下两步来完成:
第一步,估计“外部参数”。在这一步中,唯一潜在的内生变量是共同居住状态,因此使用工具变量模型确定共同居住的影响。本文在成年子女生育率回归中,将兄弟姐妹的数量作为成年子女是否与父母居住在一起的工具变量。
第二步,估计“内生参数”。包括拥挤成本、住房成本、老年护理成本和儿童看护成本,还有特殊冲击的分布。
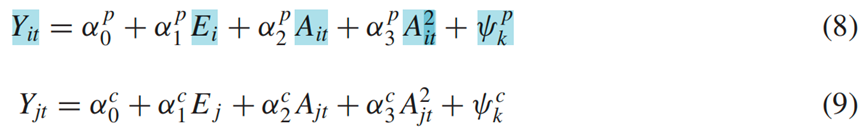
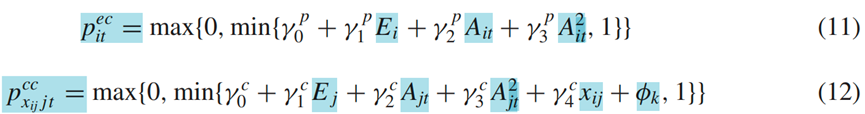
实证分析
04
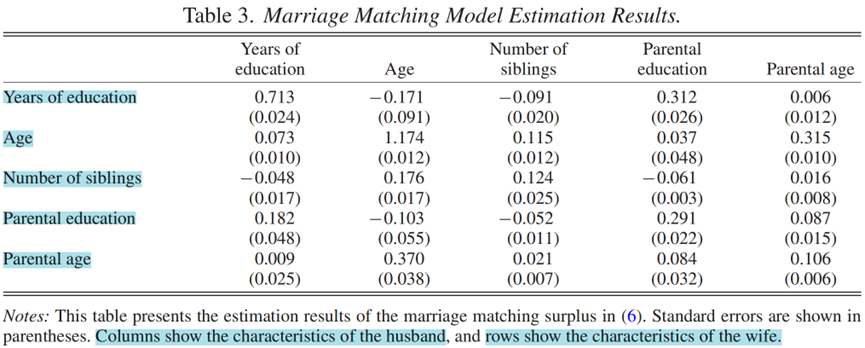
为了填补数据中缺失的婚姻关系,本文基于CFPS中的夫妻样本,估计了具有可转移效用的婚姻匹配模型。表3展示了使用矩匹配估计对夫妇特征的五个维度的估计结果:教育程度、年龄、兄弟姐妹数量、父母教育程度和父母年龄。可以看到在所有五个维度上都是正的分类匹配。
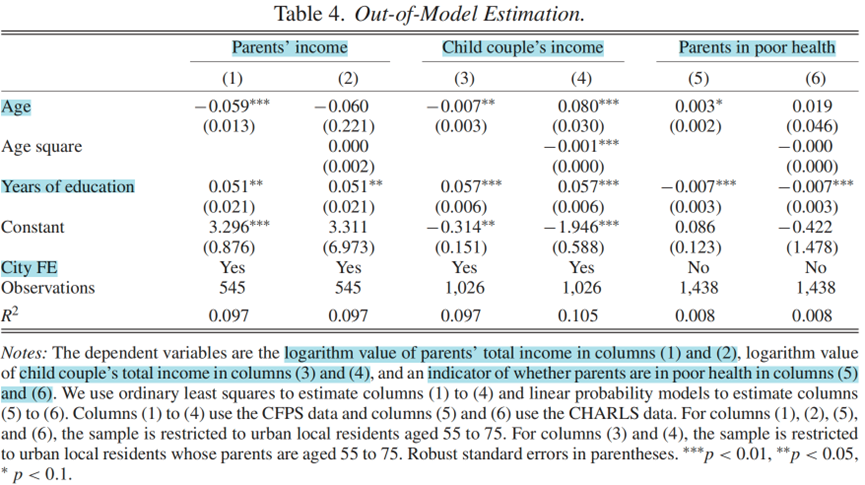
根据(8)和(9),本文使用Mincer型回归来预测父母和成年子女的收入。父母和成年子女的收入包括劳动收入和资产收入。具体地,本文将父母的对数收入(父亲和母亲的收入总和)与他们的平均年龄和受教育程度以及城市固定效应进行回归,见表4中的第(1)列和第(2)列。本文对年轻的已婚夫妇(使用他们的共同收入)进行了类似的收入回归。其结果显示在表4的第(3)列和第(4)列中。估计结果表明,父母收入随教育程度的增加而增加,随年龄的增长而减少。此外,成年子女的收入随着教育程度的增加而增加,并且具有驼峰形的生命周期特征。
根据公式(11),本文使用线性概率模型根据父母的年龄和教育程度来预测父母的健康状况。如果父母自我报告的健康状况较差,则被定义为不健康。表4第(5)列和第(6)列显示,健康状况较差的父母比例随着年龄的增长而增加,随着教育水平的下降而下降。本文还使用父母的年龄和教育程度分析了共同居住是否会影响父母的健康。
基于公式(12),使用线性概率模型,本文预测了一个家庭是否有六岁以下的孙辈,并且使用子代兄弟姐妹的数量作为共同居住的工具变量。如表5所示,在OLS和IV模型中,与父母共同居住会增加子代夫妇生下年幼孙子的机会。此外,子代生育率随着子代夫妇年龄的增长而下降,但与他们的教育成就无关。
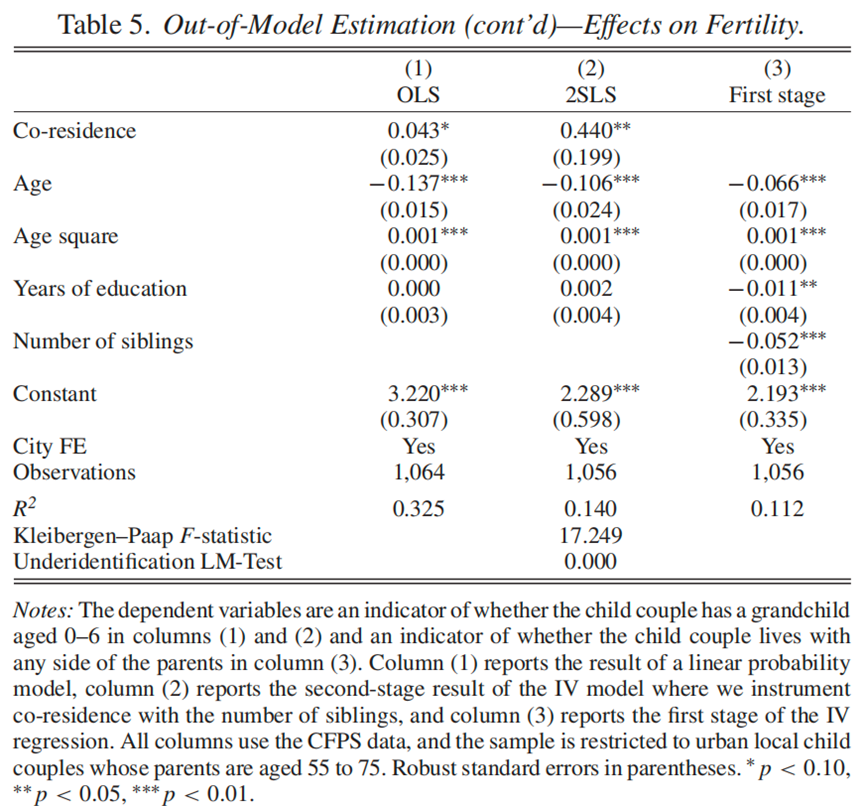
表6显示了使用间接推断的共同居住模型的估计结果。可以看到,对于年总收入为3万元的中等收入家庭的第一个出生的男性子女,拥挤成本导致共同居住盈余的损失,相当于房价下跌6.9%。相比之下,中等收入家庭的第一胎女性(非第一胎男性)子女的拥挤成本相当于房价下197.6%(32.7%)造成的共同居住盈余损失。对拥堵成本的估计表明,共同居住不仅受到经济因素的影响,还受到与社会规范相关的文化因素的影响。对于父母来说,生病概率增加1个百分点(ppt)所节省的老年护理费用,相当于房价上涨16.1%(0.548/0.034)所节约的住房费用。对于成年子女来说,生育年幼孙子女的可能性增加1个百分点所节省的育儿成本相当于房价上涨3.9%(0.133/0.034)所节省的住房成本总之,住房成本、老年护理成本和儿童保育成本的节省是家庭共同生活的重要激励因素。

05
反事实预测
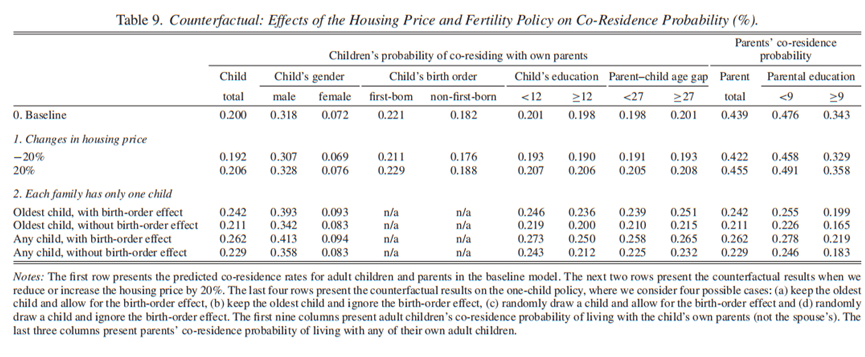
本文共设计了两个实验。第一个实验关注住房成本,假设一个城市的房价不会影响婚姻匹配。第二个实验,预测了父母只有一个成年子女时的共同居住模式。中国政府从1979年到2016年实施了独生子女政策,因此本文数据中大多数成年子女都是在实施独生子女政策之前出生的,从而能够预测在一个所有成年子女都没有兄弟姐妹的社会中,家庭的共同居住会是什么样子。在这里,总共考虑四种可能的情况:保留家庭中年龄最大的孩子并保持出生顺序效应;保留家庭中年龄最大的孩子并消除出生顺序效应;在家庭中随机保留一个孩子并保持出生顺序效应;在家庭中随机保留一个孩子,并消除出生顺序效应。该研究结果提供了独生子女政策效果的上限和下限。
表9的结果表明,房价的上涨增加了共同居住的可能性,但不同群体的影响不同。女性、第一胎或受过高等教育的成年子女以及受过高等教育父母对房价变化的敏感性更高。在不久的将来,当中国所有家庭都只有一个成年子女时,成年子女共同居住的可能性将增加,而父母共同居住的可能将大幅下降。此外,受教育程度较低的父母共同居住的可能性将大幅下降。
Abstract
We develop a co-residence model between young adults and the elderly as an application of the Shapley– Shubik–Becker bilateral matching framework. This model captures competition between adult children and between parents and parents-in-law. Using microdata from China, we estimate our model by using a network simulation method to fill in partially unobservable marriage links. We find that our model explains the child-side and parent-side competitions observed in the data better than two alternative multinomial logit models with only one-sided competition. In addition, counterfactual experiments quantify the effects of changes in the one-child policy and housing prices on intergenerational co-residence.
声明:推文仅代表文章原作者观点,以及推文作者的评论观点,并不代表香樟经济学术圈公众号平台的观点。
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 