
插图来源:midjuourney生成
原文信息:Aghion, Philippe, Antonin Bergeaud, and John Van Reenen. 2023. "The Impact of Regulation on Innovation." American Economic Review, 113 (11): 2894-2936.
DOI: 10.1257/aer.20210107
推文作者评论:
本文的理论模型非常简洁,含义清晰,实证工作非常扎实详细,简约和结构相结合,有助于进一步理解对监管政策对创新进行的影响,阿吉翁对其自90年代以来熊彼特增长模式系列研究的有力拓展。虽然和许多文献一样,研究一些门槛值对创新活动的影响,本文有一个有力的贡献是,在动态和一般均衡框架下估计一些政策对创新的长期影响,这与一些我们熟悉的文献,例如2021年AER上研究中国对创新型企业认定带来的影响的Notching R&D有所不同。
但是,本文讨论的“监管”,并不是对创新本身或者针对创新型企业的监管,而是一个基于企业雇佣规模的监管。这种情况和欧洲的很多国家很相似,那里的商业环境对经营的许多具体细节做出了细致的规定、监管并且长期比较不容易改变,因此更像是“商业环境”本身带来的监管。但在创新蓬勃发展的中美等国,更有意义的研究似乎是,针对潜在的影响,研究对新出现的、未知的技术(及其与现有技术的交互)进行的监管,对创新可能带来的市场结构变化(特别是垄断)进行的监管等等,这可能是这篇文章暂时难以回答的问题,但本文的框架具有很强的借鉴意义。
01
介绍
这篇文章研究了法规对技术创新的影响,尤其是在劳动法规举足轻重的环境中。目前,大部分的经济研究都集中在法规的静态成本(及其收益)上,而非其潜在的动态影响。
"监管"在这篇文章中指的是政府对企业与工商业行为的规定和法规,特别是劳动法规。文章提到,一些法规仅当公司达到一定规模(例如,拥有50或更多员工)时才会生效。具体的例子包括法国的劳动法规:当公司拥有50名或更多员工时,劳动法规的负担(例如,必须成立工作委员会,设立健康和安全委员会,任命工会代表等)会明显增加。因此,这种规章制度可能会阻止公司愿意创新,因为创新可能会使公司规模扩大,从而受到更强的法规约束。
识别劳动法规对创新的影响并非易事。为解决这个问题,文章利用了许多法规的规模相关性,这些法规只有在公司达到一定规模时才会生效,例如在法国,当一个公司拥有50名或以上的员工时,劳动法规的负担会明显增加。
文章用一种简单的Klette和Kortum(2004)的增长和企业动态模型形式化了这种直觉。该模型推测规模达到法规阈值的公司,在选择是否进行创新投资时,可能因为过度的规章制度而选择减少投入,导致创新减少,尤其是临近这个阈值的公司,规章制度对其影响更大。文章利用法规阈值的持续性增加成本,对我们的理论进行了测试。
文章的研究显示,法规会改变创新与公司规模的关系,尤其是对于接近法规阈值的公司。一旦规模超过这个阈值,创新与规模的关系貌似变得更加平坦,这可能是因为规模提高到阈值以上,法规对公司的影响更大,从而使公司对创新的动力减小。
文章通过对数据的量化分析,预测出法规对总体创新和福利的影响。基线估计表明,这种规定相当于对利润的2.5%的税收,降低了约5.4%的总体创新(把增长率从约2%降至1.9%)并且至少降低了2.2%的消费等效福利。法规的影响主要通过两种方式生效:首先,它降低了新公司的市场进入门槛,促使公司的规模向较小的方向发展。然后,更为重要的是,一旦公司的规模达到一定程度,法规对其的约束会抑制公司的创新活动,从而导致公司的创新水平整体降低。换句话说,大多数的总体影响是由于公司在达到某个规模后,受到法规影响,减少了对创新的投入和活动。。
然而,这篇文章对福利结果的观点保持谨慎,因为作者们提出了一个模型,该模型考虑到了公司在真正的突破性创新与小步骤、递增式创新之间做出投资决策。他们注意到这些法规政策会阻碍公司进行递增式研发,但若公司决定创新,它会倾向于尽全力创新,因为这样可以避免在规模增长的阈值附近产生停滞。
此外,作者们使用未来的引文以及基于专利文本的创新性的机器学习方法来测量,结果表明这些法规的负面影响主要限制在递增式创新的专利上。也就是说,法规似乎并没有显著抑制那些真正的突破性创新。同时,他们发现法规确实有推动创新向自动化省工方向发展的趋势,意味着公司在面临更严格法规时,可能会更倾向于寻求这类可以减少人工的创新。
因此,法规对公司决定是否进行技术创新有重大影响,并可能在长期内对经济增长造成影响。因此需要合理地设置工商业法规阈值,以避免阻碍创新和经济增长。
理论
02
这一部分展示了基于简化的Aghion (2018b)模型构建的基本理论,并在其中引入了规模相关的法规。这能够从分析的角度描述公司的创新决策如何根据其规模和法规而变化。文章通过求解包含现有市场参与者的增长和进入/退出动态的稳态企业规模分布来完成这个模型。文章展示了企业和经济的广义创新和规模如何随着法规的严格程度而变化。在整个过程中,文章探讨了这个模型对创新和就业稳定状态联合分布的含义,以及公司如何应对将在实证部分利用的外生需求冲击。
2.1 简化的Klette-Kortum模型
文章考虑了Klette和Kortum(2004)的带有企业动态的Schumpeterian增长模型的简单离散时间版本,这个版本中企业所有者只活两期。这个两期模型来自Aghion (2018b),简化了模型的描述。第一个时期,公司所有者决定投资多少在研发上。第二个时期,选择投入劳动力,生产并实现利润。在时期结束时,后代以其当前规模继承了公司,并且一个新的周期再次开始。
消费者最大化如下效用:
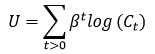
s.t.
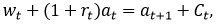
其中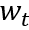 是工资,
是工资,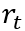 是利率,
是利率,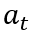 是资产,
是资产,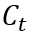 是消费。由此可得欧拉方程
是消费。由此可得欧拉方程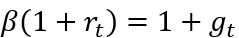 ,在平衡增长路径(BGP)上,r和g是常数.
,在平衡增长路径(BGP)上,r和g是常数.
每一期,总产品通过中间品经如下生产函数生产出来:
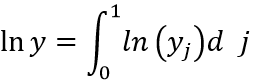
其中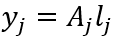 ,
,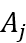 是生产率,
是生产率,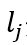 是劳动投入,那么产品的边际成本就是
是劳动投入,那么产品的边际成本就是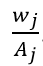 。在这里,企业被定义为生产单元(或生产线/品种)的集合,并通过成功的创新扩大产品空间。
。在这里,企业被定义为生产单元(或生产线/品种)的集合,并通过成功的创新扩大产品空间。
为了创新,一个中间品公司,结合其随时间积累的现有知识库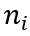 ,(它经营的种类数量)和其研发投入
,(它经营的种类数量)和其研发投入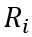 ,根据以下的Cobb-Douglas函数生产知识:
,根据以下的Cobb-Douglas函数生产知识:
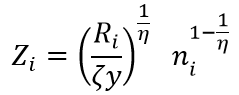
在上式中, 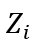 是泊松创新流的到达率,
是泊松创新流的到达率,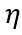 是一个凹度参数,
是一个凹度参数,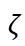 是一个规模参数。这可以推出研发成本:
是一个规模参数。这可以推出研发成本: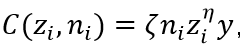 ,其中
,其中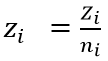 简单地定义为公司的创新强度。
简单地定义为公司的创新强度。
当一家公司在其当前的研发投入上取得成功时,它在随机选取的产品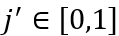 上进行创新。然后,产品
上进行创新。然后,产品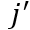 的生产率从
的生产率从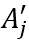 增加到
增加到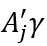 ,该公司成为产品
,该公司成为产品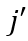 的新的垄断生产者,并因此将其产品的数量增加到
的新的垄断生产者,并因此将其产品的数量增加到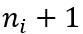 。
。
同时,其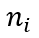 个当前产品都面临着被新进入者和其他现有公司替代的风险(称之为创造性破坏概率x)。因此,规模为
个当前产品都面临着被新进入者和其他现有公司替代的风险(称之为创造性破坏概率x)。因此,规模为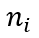 的公司的生产单位数量以概率
的公司的生产单位数量以概率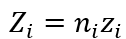 增加到
增加到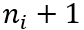 ,以概率
,以概率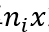 减少到
减少到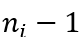 。如果一家公司失去所有的产品线,它将退出经济。
。如果一家公司失去所有的产品线,它将退出经济。
由于Cobb-Douglas加总的存在,最终产品生产者在每个品种j上花费相同的金额y。因此,最终产品生产函数对每个品种产生了单位弹性需求: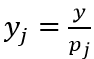 。结合在单一产品上的公司进行Bertrand竞争的事实,这表明边际成本为
。结合在单一产品上的公司进行Bertrand竞争的事实,这表明边际成本为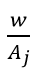 的垄断者将通过将其价格设定为前一创新者的边际成本
的垄断者将通过将其价格设定为前一创新者的边际成本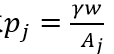 来进行极限定价。因此,产品j均衡数量和利润分别为:
来进行极限定价。因此,产品j均衡数量和利润分别为:
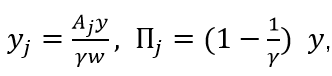
每个产品生产工人的需求则由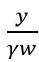 给出。公司i的就业人数等于其所有
给出。公司i的就业人数等于其所有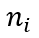 个产品中的总制造劳动力
个产品中的总制造劳动力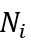 。表达式为:
。表达式为:
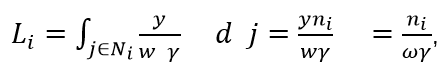
其中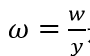 是由产出调整后的工资率,在一个BGP上这是不变的。重要的是,一家公司的就业人数严格地与其产品数
是由产出调整后的工资率,在一个BGP上这是不变的。重要的是,一家公司的就业人数严格地与其产品数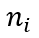 成正比。
成正比。
2.2 监管门槛与创新
下面假设当公司的劳动力超过某个门槛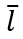 之后,会对利润征税(在法国是50人)。假设
之后,会对利润征税(在法国是50人)。假设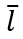 足够大,使得进入者进入时不会被收这笔税。这对应一个产品的分界数量
足够大,使得进入者进入时不会被收这笔税。这对应一个产品的分界数量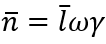 ,
,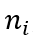 大于它就征收边际税率τ,否则不收。也就是说,额外的品种会带来额外的成本。
大于它就征收边际税率τ,否则不收。也就是说,额外的品种会带来额外的成本。
一个规模为n的公司因此选择创新强度z,以最大化期望净现值:
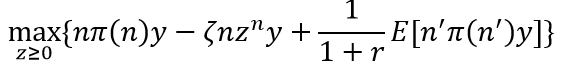
其中,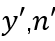 表示第2期时的产量和品种数。
表示第2期时的产量和品种数。
当创新强度为正时,最优创新强度可以被写作:
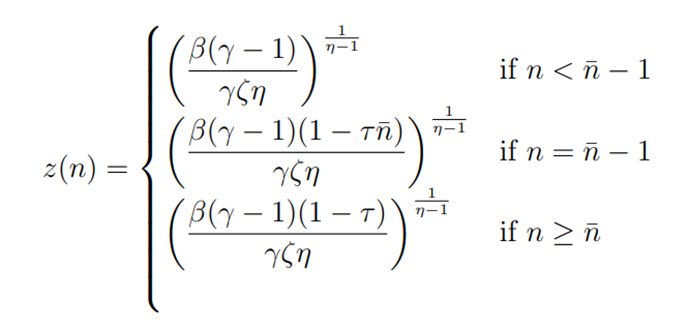
本文的大部分经济含义都可以由该式得到。创新强度z(n)对于远低于阈值的小型企业来说是最高的(右侧第一行),对于超过阈值的大型企业来说是第二高的(第三行),对于刚好在阈值左边的中型企业来说是最低的(中间一行)。数据中能观察到的是总创新(以专利数量为代表),即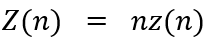 。由于就业与产品数量成正比,这意味着创新规模关系的斜率将取决于企业是高于还是低于监管门槛。典型地,创新和公司规模之间的向上倾斜关系对于小公司来说应该比大公司更陡峭,并且应该在阈值处不连续地下降和变平。此外,大型企业与小型企业的创新规模关系的斜率之比,与模型的基本参数直接相关,特别是与监管税有关。文章接下来将利用这一事实来经验地确定监管税的规模,然后将其用于估计监管对创新的总体影响。
。由于就业与产品数量成正比,这意味着创新规模关系的斜率将取决于企业是高于还是低于监管门槛。典型地,创新和公司规模之间的向上倾斜关系对于小公司来说应该比大公司更陡峭,并且应该在阈值处不连续地下降和变平。此外,大型企业与小型企业的创新规模关系的斜率之比,与模型的基本参数直接相关,特别是与监管税有关。文章接下来将利用这一事实来经验地确定监管税的规模,然后将其用于估计监管对创新的总体影响。
2.3 管制门槛与企业规模分布
接下来看企业规模的稳态分布,并看这一分部如何受到管制税影响。令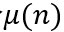 为n个产品的企业的比例。对于任意n>1,稳态条件可以写作这一规模的企业进出相等,即:
为n个产品的企业的比例。对于任意n>1,稳态条件可以写作这一规模的企业进出相等,即:
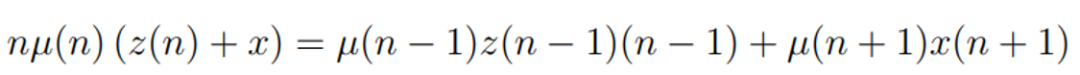
由定义,有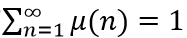 。另外,创造性破坏的速率,等于创造性破坏的进入者进入的速率,加上现有生产者创新速率z(n)的加权平均,也就是:
。另外,创造性破坏的速率,等于创造性破坏的进入者进入的速率,加上现有生产者创新速率z(n)的加权平均,也就是:
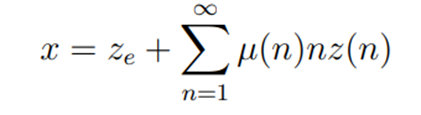
2.4 模型求解
作者用数值方法求解模型。有以下几个发现:
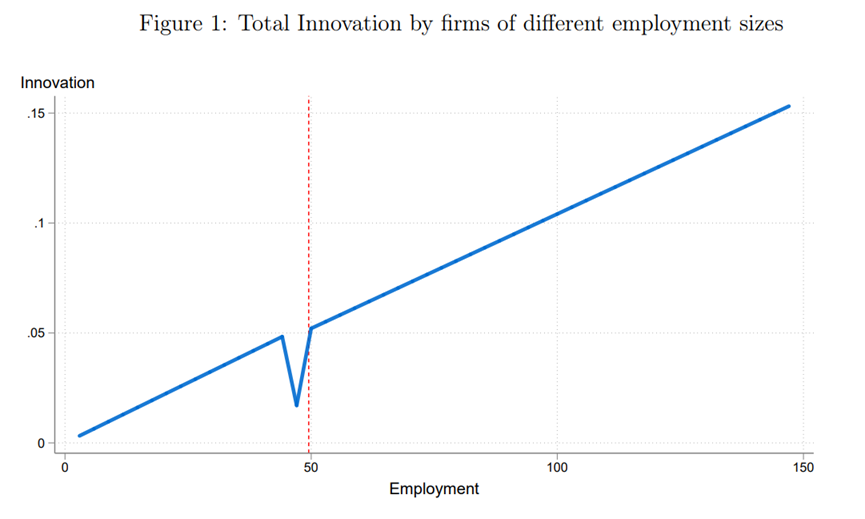
(1) 公司层面的创新随着公司规模线性增长,直到公司接近监管门槛,在这一点上有一个明显的创新谷。在此之后,一旦企业越过门槛,创新又会随着企业规模的增加而增加(图1)。
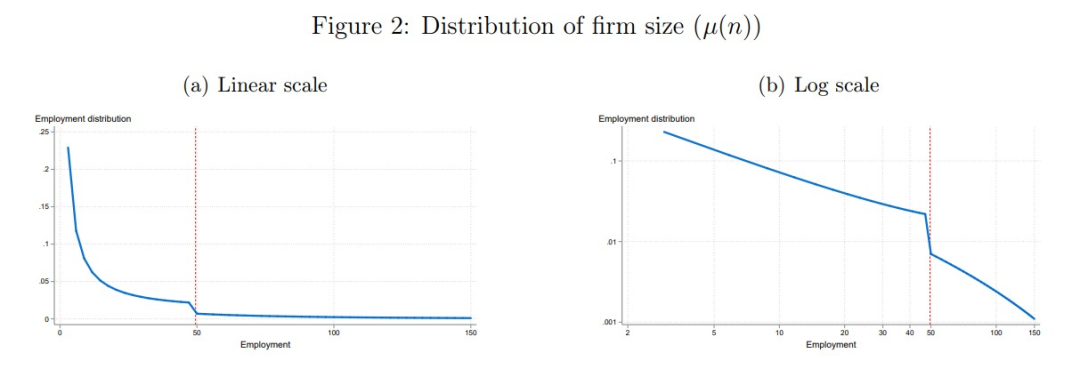
(2) 图2绘制了均衡企业规模分布,即每个企业雇佣水平的密度µ(n)值。图(a)使用线性标度,但由于分布是非线性的,图(b)以对数-对数标度来绘制它,图(b)中它大致是对数线性的,符合(Axtell, 2001)和其他许多人记录的众所周知的幂律)。请注意,在监管阈值附近与幂律的背离。当公司数量接近50时,分布会略微膨胀,然后不连续地下降,一旦公司超过阈值,就会再次下降。与创新规模不连续不同,法国规模分布中的这种“破幂律”在之前的文献中已经被注意到(例如Ceci-Renaud and Chevalier, 2011),但事实证明,在没有内生创新的模型中,这种形状很难完全合理化。
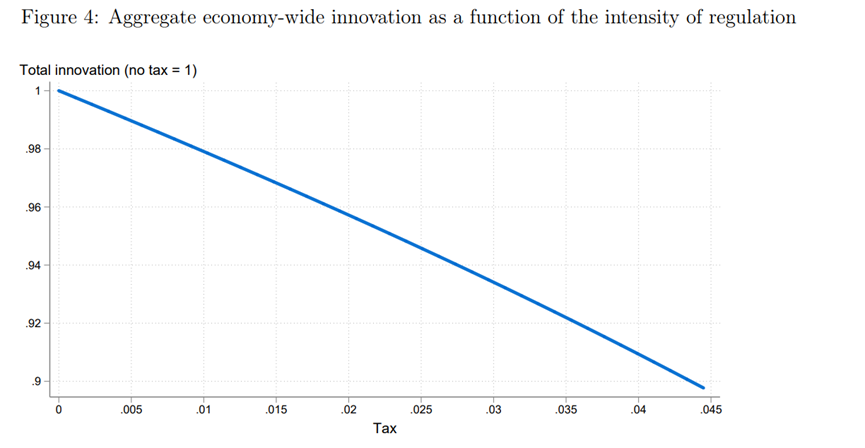
(3) 图4显示了受监管经济中总创新的下降,与反事实的不受监管经济(我们将总创新归一化为1)相比。创新下降的幅度明显随着监管税τ的强度而增加。例如,如果τ = 0.02而不是零,则总创新减少4%。总体创新的下降有三个原因。首先,对于给定的企业规模,税收增加对门槛左边的企业的创新有很强的负面影响,对门槛右边的所有企业的创新有较小的负面影响。其次,增税减少了大公司的数量,而这些大公司也会进行更多的创新。第三,创造性破坏的减少,因为更高的税收意味着更少的进入(因为所有进入者都需要创新来取代在位者)。当使用数据来量化模型时,文章将总创新的下降分解为这些不同的元素,并表明第一个元素(在位者创新)占主导地位。
2.5 需求冲击的影响
在下面的动态分析中,文章将研究市场规模冲击对创新的影响。考虑对产品j的特有的市场规模冲击,在模型上下文中表示为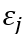 ,然后,产品j的均衡产出和就业分别受到
,然后,产品j的均衡产出和就业分别受到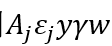 和
和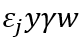 的冲击。因此,在保持创新固定的情况下,
的冲击。因此,在保持创新固定的情况下,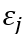 在短期内对企业规模有正的影响,并且对于阈值左侧的企业,这种影响较小,因为这些企业不希望越过阈值并承担额外的监管成本.
在短期内对企业规模有正的影响,并且对于阈值左侧的企业,这种影响较小,因为这些企业不希望越过阈值并承担额外的监管成本.
那么,冲击对企业层面创新的影响是什么?它相当于在最优创新规模的每一项前面乘以冲击项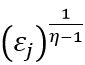 来进行修正。对于那些远低于监管门槛的小企业来说,这种冲击对创新强度的影响最大。第二大影响将是在门槛右边的大公司的创新。而需求冲击的最小影响只会出现在门槛以下的公司身上。
来进行修正。对于那些远低于监管门槛的小企业来说,这种冲击对创新强度的影响最大。第二大影响将是在门槛右边的大公司的创新。而需求冲击的最小影响只会出现在门槛以下的公司身上。
03
实证
3.1 数据
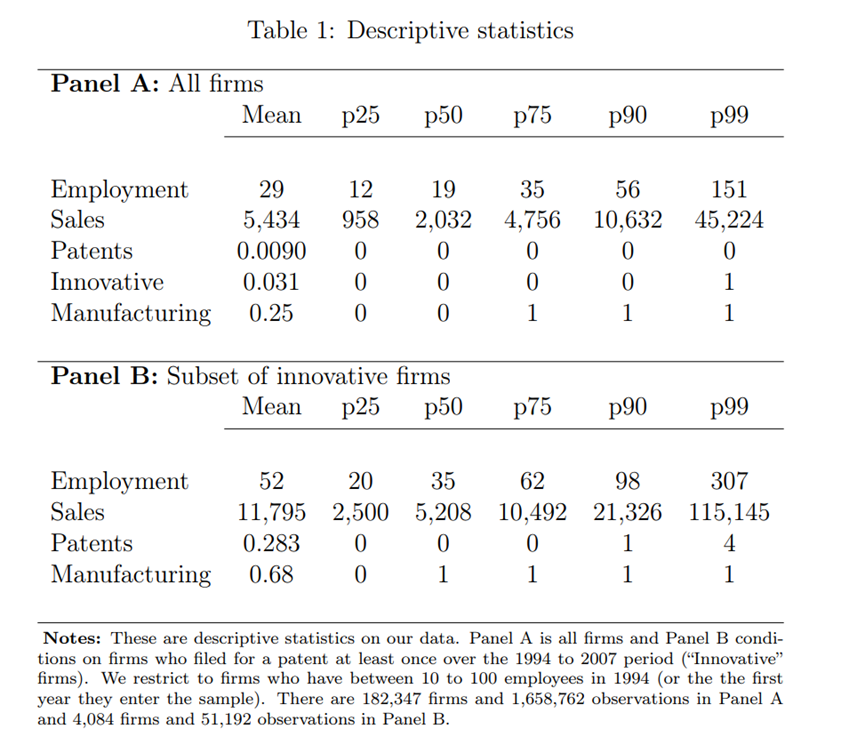
主要数据来自法国税务机关,他们从1994年到2007年每年收集所有法国公司的资产负债表信息(“FICUS”)。文章限制只关注非政府企业,并从Lequien (2017)那里获取了专利信息。这将使用一种算法将PATSTAT(2016年春季)数据库与FICUS进行匹配,该算法将专利首页上的关联公司(知识产权持有人)的名称与名称和地址最接近专利持有人的公司的名称和地址进行匹配。对于员工少于10人的公司,算法的准确性更差,因此文章关注的是员工超过10人的公司。由于文章感兴趣的是一项法规对超过50名员工门槛的公司的影响,因此文章进一步限制在对1994年(或这些公司出现在数据中的第一年)拥有10至100名员工的公司。
主要样本包括182,348家不同的公司和166万个观察值。表1报告了一些基本的描述性统计数据。可以看到,企业平均每年申请0.009项优先专利,如果是创新者,每年申请0.28项。众所周知,创新的分布是高度倾斜的,在样本中,少数公司拥有大部分专利。然而,由于数据中没有包括最大的法国公司,所以这种偏差不太明显。
3.2 动态分析
这个估计的核心思想是,使用外生需求变化(主要是海外需求变化)作为外生冲击,检验它与监管门槛的交互效应,也就是一个广义的DID。
3.3.1估计方程
接下来估计一个如下的回归:
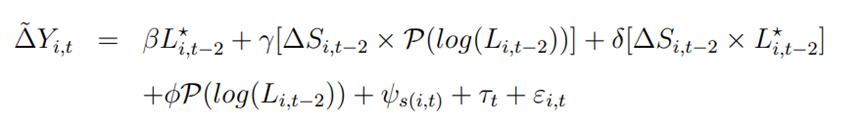
其中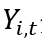 是创新的估计,
是创新的估计,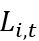 是雇佣数量的估计,是虚拟变量,若接近但低于监管边界则为1,在数据中是45-49人。
是雇佣数量的估计,是虚拟变量,若接近但低于监管边界则为1,在数据中是45-49人。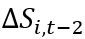 是对市场规模的外生需求冲击,会引发模型中创新的增加。
是对市场规模的外生需求冲击,会引发模型中创新的增加。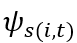 是行业虚拟变量。
是行业虚拟变量。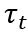 是时间虚拟变量,
是时间虚拟变量,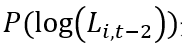 是
是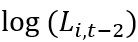 的多项式。
的多项式。
其中,因变量定义为创新Y的增长率:
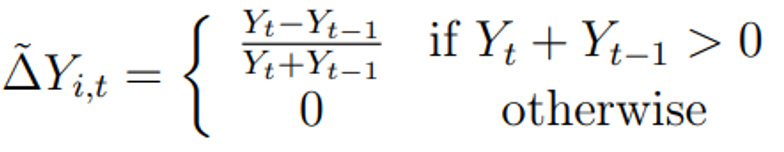
这里最关心的系数是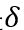 ,预计会是负的。较大的公司可能会对给定的冲击做出更大的反应,但这种关系应该会在阈值左侧的公司中破裂,因为这些公司更不愿意越过阈值以应对积极的市场规模扩张。
,预计会是负的。较大的公司可能会对给定的冲击做出更大的反应,但这种关系应该会在阈值左侧的公司中破裂,因为这些公司更不愿意越过阈值以应对积极的市场规模扩张。
3.3.3 模型主要预测的检验
下面是创新偏移量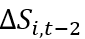 的构建。根据Hummels et al.(2014)和Mayer et al.(2016),文章依靠国际贸易数据来构建(出口)需求冲击。简而言之,我们通过衡量从全球所有国家(法国除外)进口的变化,来观察外国对某一特定产品的需求如何随时间变化。然后,我们为每个法国公司i建立了一个产品/目的地组合,并通过该产品对公司i的相对重要性来衡量每种产品的国外需求。更具体地说,定义了公司i在日期t的出口需求冲击
的构建。根据Hummels et al.(2014)和Mayer et al.(2016),文章依靠国际贸易数据来构建(出口)需求冲击。简而言之,我们通过衡量从全球所有国家(法国除外)进口的变化,来观察外国对某一特定产品的需求如何随时间变化。然后,我们为每个法国公司i建立了一个产品/目的地组合,并通过该产品对公司i的相对重要性来衡量每种产品的国外需求。更具体地说,定义了公司i在日期t的出口需求冲击
为了估计上述方程,需要在使用数据集时做一些进一步的限制。
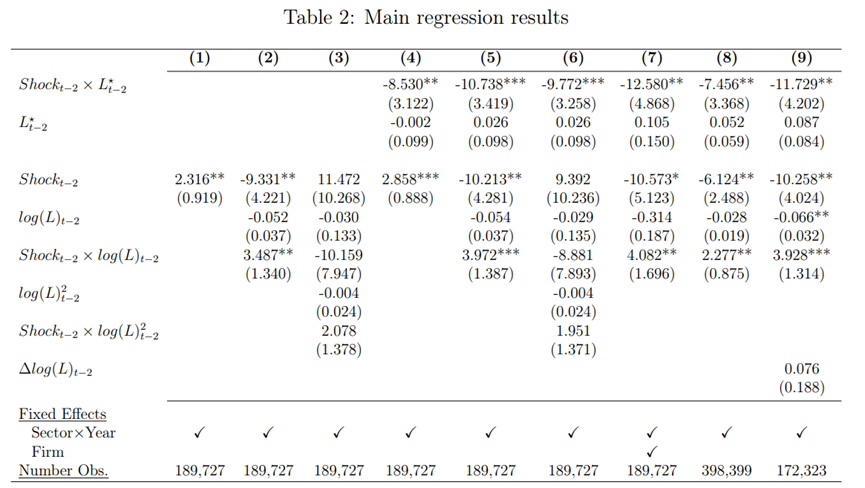
首先,请注意,市场规模冲击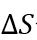 仅定义为出口企业,即1994年至2007年在海关数据中至少出现一次的企业。其次,为了提高冲击测量的准确性,文章限制了对制造业的关注。不仅很大一部分专利活动位于制造业,而且这些公司也更有可能参与其出口商品的生产(见Mayer ,2016)。因此,主要回归样本由24,081家公司和189,727个观测值组成。
仅定义为出口企业,即1994年至2007年在海关数据中至少出现一次的企业。其次,为了提高冲击测量的准确性,文章限制了对制造业的关注。不仅很大一部分专利活动位于制造业,而且这些公司也更有可能参与其出口商品的生产(见Mayer ,2016)。因此,主要回归样本由24,081家公司和189,727个观测值组成。
表2给出了方程的估计结果,即对滞后市场规模冲击下企业专利增长率的回归。
列(1)显示,面对正向外生出口冲击的企业显著更有可能增加其创新活动。该系数表明,市场规模每增加10%,专利数量就会增加约3%。
列(2)包括对滞后水平(就业)及其与冲击的相互作用的控制。相互作用系数为正且显著,表明大公司比小公司对冲击的反应更大。虽然没有直接的因果关系,但这是2.5中讨论过的。
列(3)通过在滞后就业及其与冲击的相互作用中加入二次项来一般化这一影响。
列(4)返回到列(1)的更简单的设定,并包括一个虚拟变量,用于在t-2时,公司的就业人数是否刚好低于45-49名员工范围(定义为L)的监管阈值,以及这个虚拟变量与冲击的相互作用。我们的关键系数在这个相互作用项上,正如我们的模型所表明的那样,它显然是负的和显著的。这是主要结果之一:与远离监管门槛的公司相比,刚好低于监管门槛的公司的创新对积极需求机会的反应要小得多。文章解释是,当一家企业接近就业门槛时,由于员工人数超过50人的监管成本,它面临着巨大的“增长税”。因此,这样的企业将更不愿意投资于创新,以应对这一新的需求机会。该公司甚至可能干脆完全削减其创新活动,以避免跨越门槛的风险。
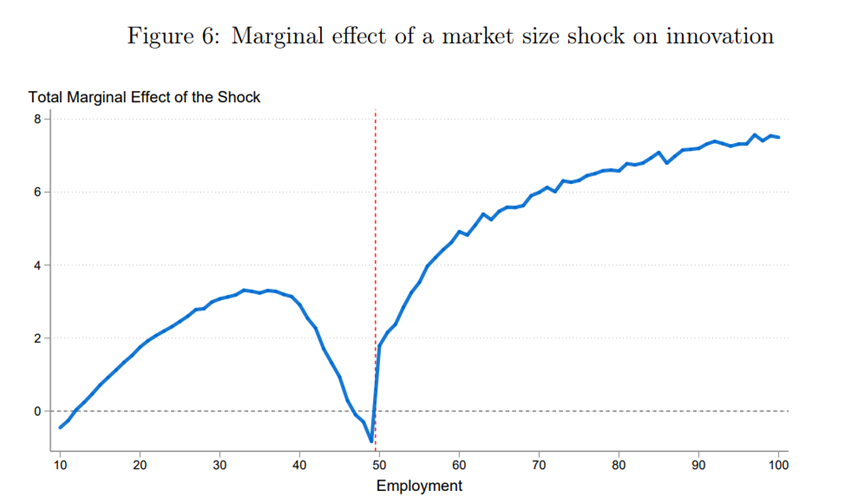
图6中描述了创新和冲击之间的关系。该图使用表2列(5)中的系数绘制了不同企业规模下市场规模冲击对创新的隐含边际效应。可以看到,大公司的创新往往比小公司对出口冲击的反应更积极,但在监管门槛处,需求冲击的边际效应急剧下降,这与模型一致(例如,见第2.5节)。可能的情况是,阈值和冲击之间的负相互作用可能是由于一些忽略的非线性。因此,在第(5)栏中,额文章还包括了滞后就业及其与冲击的相互作用(如第(2)栏)。这些确实具有解释力,但关键交互系数仍然是显著的和负的,文章将其视为首选设定。
列(6)在列(3)之后添加了一个二次项及其相互作用。关键交互效应仍然显著,这些额外的非线性不显著。
文章随后进行了一些额外的探讨,包括监管对创新的总体效应,监管的总福利效应,以及通过进一步细化的数据,探讨对不同类型的创新(主要是渐进创新、激进创新和劳动力节约型创新的影响),并把均衡工资内生化。这主要是通过校准(Calibration)实现的。感兴趣的读者可以阅读原文。
结论
04
在本文中,我们开发了一个框架来分析监管对创新的影响。我们将此应用于法国,在那里,严格的劳动法规影响到雇用50名或更多工人的公司。我们在理论和经验上都表明,这些监管成本的前景阻碍了刚刚低于门槛的公司进行创新,在门槛下,创新是通过专利申请量来衡量的。当非参数地观察阈值附近的专利密度时,以及在我们检查企业对外生市场规模冲击(来自出口市场)的异质反应的参数练习中,这种关系都会出现。平均而言,企业在经历积极冲击时创新更多,但当企业刚好低于监管门槛时,这种关系显著减弱。然后,我们使用我们的数据和文献中的矩来校准模型中的结构参数。例如,使用研发成本函数的估计,我们可以从大公司与小公司的创新规模关系斜率之间的比率中推算出监管税的大小。我们的基线估计表明,总创新(因此增长)损失约为5.4%,福利损失的下限约为2.2%。这表明,与现有的将技术视为外生因素的分析相比,福利损失更大。
对这一结论的一个警告是,当我们使用引用信息时,我们发现劳动法规阻碍了渐进式创新,但对更激进的创新几乎没有影响。这与模型的概括一致,该模型允许同时投资于两种类型的研发,并略微减轻了监管的福利损失。本文的分析可以在几个方向上进行推广。首先,我们在本文中关注的是长期稳态,但分析政策变化引发的转型动态,并考虑调整成本,可能同样重要。其次,该框架可以适用于许多其他国家和监管环境。第三,我们的分析仍然集中在劳动法规的成本上。然而,这样的监管也可能以更好的保险和员工更深入地参与公司管理的形式带来好处,这反过来又促进了雇主和员工之间的信任。未来的工作应该考虑到这些好处,看看它们是否足以克服我们在这里确定的成本。
推文作者:
韦忠吉,香港中文大学经济学系博士生。研究兴趣:宏观经济学,金融经济学。邮箱:
Abstract
We present a framework that can be used to assess the equilibrium impact of regulation on endogenous innovation with heterogeneous firms. We implement this model using French firm-level panel data, where there is a sharp increase in the burden of labor regulations on companies with 50 or more employees. Consistent with the model's qualitative predictions, we find a fall in the fraction of innovating firms just to the left of the regulatory threshold. Furthermore, we find a reduction in the innovation response of firms to demand shocks just below the threshold. Regulation reduces aggregate innovation by 5.7 percent.
声明:推文仅代表文章原作者观点,以及推文作者的评论观点,并不代表香樟经济学术圈公众号平台的观点。
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 