原文信息：Moretti, Enrico. 2021. "The Effect of High-Tech Clusters on the Productivity of Top Inventors." American Economic Review, 111 (10): 3328-75.DOI: 10.1257/aer.20191277

图片来源：谷歌图片

摘要

高科技产业聚集在少数城市，在美国，前十个大产业集群中计算科学、半导体、生物行业发明人数量分别占所有美国发明人总数的69%，77%和59%。本文使用109846个发明人的面板数据，研究发现地理集聚对产出有显著影响。当发明人所处的研究领域不变，他从集群规模相对较低的城市转移到相对较高的城市，其专利产出和专利质量都有显著提高。生产率外部性的存在意味着发明家的地理集聚催生了美国整体创新活动的巨大收益。

01  引言

从常识出发，团队互动对个人生产率的影响至关重要。这种外部驱动力对类似于艺术和科学等所有的创造性职业都是如此（Lucas，1988）。

创新企业具有按照研究领域进行集聚的特点和趋势（Carlino et al. 2012）。例如，位于美国西雅图的微软和亚马逊、波士顿的生物医药研究、奥斯汀的软件和通讯、罗利-达勒姆的制药企业、匹斯堡的自动驾驶企业和硅谷的大量的创新企业。地理集聚现象的出现不仅仅是因为好奇的驱动，它有更深更重要的城市和州的内涵。高技术产业的集聚是当地创新型产业实现增长的重要驱动力。为了吸引更多的高技术产业落户，各地区出台了一系列的激励政策。例如，政府对迁移到本地的公司实行补贴政策。从数量上看，各研究领域高技术产业的空间集聚具有十分显著的特征。

研发领域创新活动的集聚对高科技部门地理上的经济性提出了全新的问题，因为高科技产业集群通常坐落于具有高劳动力和房地产成本的城市，如旧金山、波士顿和西雅图。高科技产业的发明家在高成本的情况下，缘何倾向于选择靠近相同领域发明家的位置？这对创新有什么样的影响？Marshall (1890)提出，集聚可以提高生产效率，产业集聚会使得贸易不在成为秘密。Lucas (1988) 提出了集聚的生产率效应，其将促进本地知识的溢出，提高劳动力和企业的匹配程度。从经验来看，确定硅谷式集聚的生产率优势是非常困难的。首先，位置是内生的，因为工人和公司根据诸多可观测到和未观测到的因素。其次，对于工人生产率的直接度量是非常罕见的。

本文使用基于1971年至2007年间在美国申请专利的顶级发明家的面板数据探究了两个问题：①对于硅谷式集群的发明家来说是否具有生产率优势？②地理集聚对美国整体创新的总体效应是什么？本文定义的集聚为城市和研究领域两个层面。本文估计了发明家的生产率如何随相关集群的规模而变化，通过同一城市和领域的其他非重点发明家的数量来衡量。同时，使用一年内的专利产出量以及引用量测度生产率，其中引用量是对专利质量的衡量。本文的重点为顶级发明家，其被定义为专利数量总数的前10%。

本文的研究主要分为三个部分：

第一，研究发明家在纽约州罗切斯特的经历，高科技产业集群由于柯达的倒闭而衰落，柯达的倒闭对罗彻斯特高技术集群产生了广泛深远的影响，发明家数量较其它城市下降了49.2%。由于本次冲击非罗彻斯特本地的经济因素驱动，而是由于数码摄影的出现引起，因此其具有相对外生性。以所有领域的发明家数量衡量，其规模相对于其他城市下降了49.2%，受柯达缩减规模的拖累。这次冲击是巨大的，可以说是外生的，因为它是由数码摄影的出现引起的，而不是罗切斯特当地经济特有的因素。因此，罗彻斯特的经验提供了一个有趣的案例研究，以验证高技术产业集群规模影响发明家生产力的假设。特别是，研究罗彻斯特高科技产业集群的突然崩溃如何影响柯达以外的发明家，可以直接检验集群规模对生产率的影响。如果发现当地高科技集群消亡后，它们的生产率没有发生变化，则会对生产率取决于集群规模的假设可能存在问题。采用1996年和2007年罗彻斯特的数据，研究发现，随着罗彻斯特高科技产业集群的衰落，罗彻斯特的非柯达发明家相对于其他城市的非柯达发明家，经历了巨大的生产力损失。这与地理集聚导致的高科技部门存在重要的生产力溢出的研究结论具有一致性。

第二，对涵盖了1971-2007年109849位发明家895个集群的全样本数据进行分析。研究发现，当一个发明家转移到一个更大的集群时，她会经历一年内产生的专利数量和质量的显著增加。根据动态响应模型的研究结果，研究发现生产力的增长是在移动之后，而不是在移动之前。没有证据表明未来的处理值会影响当前的生产率。基于在多个城市设有实验室公司的地理结构构造工具变量（IV），使用集群外本地企业扩张来预测本地集群规模。2SLS模型的估计结果表明，集群规模的增加导致了生产率的提升。研究发现，与较小集群中的类似发明人相比，平均来看，转移到较大集群的发明人往往会引用更多专利，尤其是本地专利。由于发明人的引文可以说是发明人了解特定创新的标志，因此这一发现表明，转移到大型集群会导致对现有创新，尤其是本地创新的更多了解，也证明了更大的集群可以更加允许知识和思想的更有效传播。研究可以用来量化特定企业在集群内产生的溢出效应，对特定企业在特定集群中产生的生产率溢出进行估计，对提供补贴以吸引高科技企业进入其管辖范围的地方和州政府具有借鉴意义。

第三，本文尝试量化对美国整体而言集聚的宏观效益，使用估计的生产率与集群规模的弹性来研究地理集群对美国专利总量的贡献。特别是，与发明人在各个地区分布更为平均的情况相比，每个领域的发明人集中在少数几个地方，是否会使该国每年专利产出总量增加？本文将观察到的美国每个领域每年产生的专利总数与如果发明人质量和公司质量没有改变，但一些发明人在空间上从大集群重新分配到小集群，直到每个领域内的集群规模在城市之间相等时，将产生的专利数量进行比较。由于集聚对生产率的影响，这种空间再分配将提高小于平均值的集群中发明人的生产率，降低大于平均值的集群中发明人的生产率。总的来说，这种空间再分配对整个国家的总体影响的大小取决于小集群的收益与大集群的损失的相对大小。从经验上看，集聚显著提高了聚合效率。虽然高科技产业的空间集聚可能加剧美国城市之间的收入不平等，但这对美国的整体创新生产也很重要。寻求吸引高科技投资的政策可能有助于减少收入差距，但总的来说成本很高，这创造了一个典型的公平效率权衡的案例。

02 数据

2.1 专利、发明家及所处位置

专利数据来源于COMETS (Connecting Outcome Measures in Entrepreneurship, Technology, and Science)数据库，其中涵盖了美国1971-2007年共4229809项专利及引用数据。根据the Bureau of Economic Analysis’s(BEA)的分类标准，可以将美国划分为179个经济区域（下文统称为城市），并将每位发明家与其所在的城市相匹配。专利中的地址既有具体发明家的住址，也有其公司的地址。因为公司的地址不能反映专利前期研发所处的位置，所以选取发明家居住地址。专利主要涵盖了5个研究领域，分别是半导体、计算科学、生物化学、其他工程、其他科学。专利技术等级可分为579个。专利数量的计算根据的是申请数量，而非授权数量。专利的引用数据为被引而非施引。当多个发明人共有一个专利时，平均分配专利数及引用数。本文重点关注在样本期内发明专利数量位于前10%的“明星发明家”。

2.2 集群

集群定义为城市和研究领域的组合体，本文的观测范围涵盖36个年份、179个城市和5个研究领域。集群规模的度量定义为当年在某个集群的全部发明家的生产率占当年该领域全部发明家生产率的比例。计算科学发明家的地域集中非常明显，生物化学总体上的集中程度低于计算科学，半导体行业的集中程度最高。

2.3 数据的局限性

局限一：发明家的创新活动仅采用单一的专利数量衡量存在一定的缺陷。某些专利代表了该领域的重要创新，但部分专利可能代表了不具备重要意义的创新活动。为了弥补这一缺陷，本文同时采用后续引用(subsequent citations) 测度专利质量。并非所有的创新转化为专利形式，同时不少专利是跨研究领域的。不同行业申请专利的动机也存在不一致性。基于上述原因，本文在模型中控制了研究领域和年份、技术类别和年份的联合固定效应。一个可能存在的现象是，不同集群规模可能导致的创新专利申请倾向不同，出现大集群专利的边际价值低于小集群的情况。

局限二：每位发明家可能并不是在每一年都申请专利，这导致了样本的选择性偏差。为了尽可能减少偏差，本文重点关注的是专利申请量较大、每年或大多数年份有专利产出的明星发明家(Star inventor)。由于无法观测到专利申请量为0的发明家，所以集群规模对专利数量影响的回归分析量化了集群规模对发明家生产率的影响（集约边际），而忽视了集群规模对专利申请概率的影响（广延边际）。如果集约边际和广延边际同向发展，那么本文的估计应该被解释为集群规模对专利总效应的下限。为了实证检验偏差的方向和程序，本文提供了两条证据。第一，通过插值法对专利数量为0的样本进行插值；第二，对不同时间单元检验其敏感性。

03 柯达消亡对罗彻斯特的

高技术集群发明家的影响

研究硅谷式集群相对小集群的的生产率优势，一种可靠的方法是利用外生于当地经济的高技术集群的变动冲击。部分美国科技集群的兴衰提供了有趣的研究案例。罗彻斯特主要的高科技公司柯达的倒闭导致了高科技集群规模的变化，具有相对的外生性。在20世纪80年代到90年代，柯达是照相机胶片的主要生产者，是美国专利最多的公司之一。在1971至2007年间，柯达的专利申请量位居第五。1996年，柯达占罗彻斯特发明家总数的49%。在1996年之后，这一数量急剧下降，主要是由于数码摄影普及，对实物胶片的需求量大大下降。

根据下图可以看出，1990年以来，柯达股价的最高点位于1996年。在1996至2007年之间，柯达的股价下降了82%。在1997年，在罗彻斯特柯达发明家的数量为1254，到2007年仅有204。

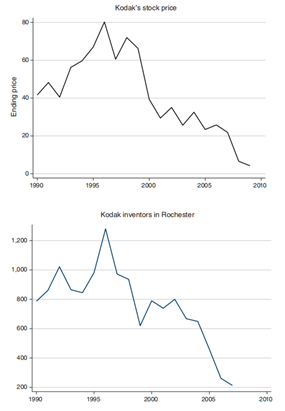
具体而言，本文检验了由柯达消亡导致的罗彻斯特高技术集群规模变化对非柯达发明家生产率的影响。这一冲击是巨大的，并且具有相对外生性。如果罗彻斯特高科技集群遭受巨大负面冲击后，发现柯达以外的发明家的生产率没有改变，那么集群规模变化导致生产率变化这一假设是否成立将会产生疑问。

基准估计。下图直观展示了1990-2007年间罗彻斯特非柯达发明家的平均生产率。垂直红线表示1996年柯达股价的峰值。虽然平均生产率在1996年之前基本持平，但是在1996年之后出现了显著的下降。

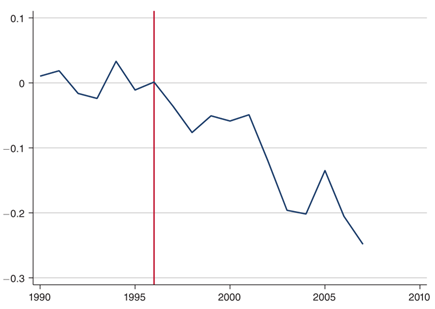
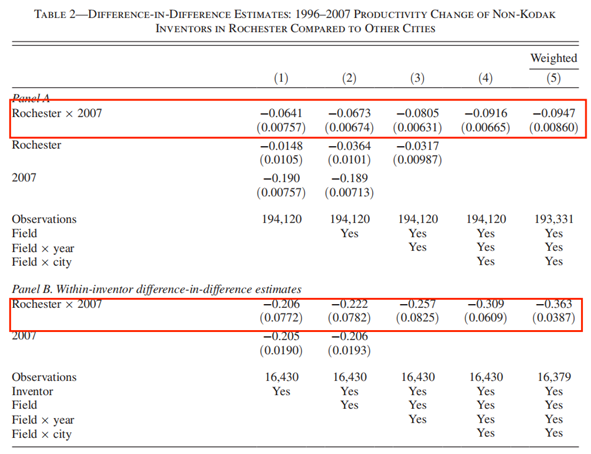
表2为运用DID方法对罗彻斯特非柯达发明家和其它城市非柯达发明家经历的变化进行比较。表中的两个面板有所不同，面板数据A基于横截面比较，面板数据B使用数据的纵向性质，重点关注发明人组内内部生产率的变动（1996年在柯达所处的五个主要的研究领域中，没有一个未受其消亡的影响。下一节中将使用所有城市和年份进行研究，将能够识别在集群规模中特定领域的变化）。样本包括1996和2007年，因为1996年为柯达股票价格的最高点，而2007年为数据可得的最后一年。

在面板A第（1）列中，将2007、罗彻斯特作为虚拟变量及交互性纳入回归方程。罗彻斯特虚拟变量的系数意味着罗彻斯特非柯达发明家的平均生产率在统计意义上是不同于其它城市的。本文关心的是交互性的系数，它意味着罗彻斯特非柯达发明家一年内专利申请的平均数量较其它城市下降了6.4%。在（2）-（4）的回归中，加入研究领域、研究领域和年份、研究领域和城市的固定效应。回归中剔除了Xerox发明家，结果依然稳健。回归（5）中汇报了这个权重估计。根据罗彻斯特受到冲击前可观测的城市变量，权重反映了重点发明家城市到罗彻斯特“距离”。

发明家组内估计。由于面板A为截面数据，估计可能存在一些问题，一方面，可能存在由于发明家自选择问题导致的未观测到质量变化的可能性。另一方面，由于当地高技术产业收缩，一些优秀的非柯达发明家离开罗彻斯特；由于柯达裁员，罗彻斯特地区的其它公司可能会雇佣柯达的发明家。

在面板B中，本文使用平衡性面板数据进行估计，比较了罗彻斯特和其它城市发明家组内的生产率变化情况。在（1）列中仅控制发明家层面的固定效应。估计结果表明，在1996年，位于罗彻斯特的发明家较其它城市的发明家生产率下降了20.6%，相继控制研究领域、研究领域和年份、研究领域和城市固定效应。（5）为权重估计，负向作用更为明显。

柯达供应商。由于柯达的消亡，柯达产品供应商的需求也可能随之下降。如果产品需求下降导致了柯达供应商更低的发明家生产率，在原则上这将可以解释在柯达消亡后罗彻斯特发明家生产率的下降。在这种情况下，我们希望从罗彻斯特生产率损失的估计中排除供应商对生产率的影响。供应商生产率的下降也可能是柯达消亡的内生效应。

总体来说，本文得出的结论是随着罗彻斯特高技术集群产业的衰落，罗彻斯特非柯达发明家较其它城市的非柯达发明家而言经历了巨大的生产率损失。然而这并非生产率溢出效应的直接证据，但这与集群规模影响发明家生产率的假设具有一致性。

04  发明家生产率与企业规模

罗彻斯特的分析聚焦了一个特定的冲击，本部分我们将关注的重点转向发明家生产率和集群规模之间的关系，运用所有城市、研究领域和年份的样本数据。本文假定集群内发明家的生产率取决于技能、位置、集聚效应和特定因素，模型如下：

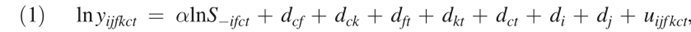
其中，t代表年份，i代表发明家，j代表公司，f代表研究领域，k代表技术等级，代表城市。yijfkct专利数量，S(-ifct)为不含发明家i集群规模的大小。dcf、dck代表城市和研究领域、城市和技术等级效应，为了吸收可能使特定领域或特定技术类别在某些地区使得生产率偏高且不随时间变化的因素。dft、dkt吸收全国范围内随时间变化的技术和行业变化。dct吸收一个地区所有领域共享的生产率决定因素在城市层面的变化；di、dj发明家和公司层面的效应。如果集群规模促进了发明家生产率的提升，则α大于0。OLS回归要求随机扰动项和解释变量之间为正交关系。

在上述的估计中可能存在两个担忧：分类（或内生的劳动力质量）和联立（或内生的劳动力数量）。

第一，发明家对集群的选择效应，高产的科学家可能更倾向于分布在大集群中。由于本文控制了城市和年份的联合固定效应，吸收了全部城市层面的特征和永久性、时变性因素。当地基础设施的内生性变化为联合固定效应吸收，因此当地基础设施水平不会影响正交条件。不随时间变化因素导致的科学家在特定行业和位置的分类担忧也可以被解释，城市和研究领域的联合效应控制这种类型的生产率差异。由于随时间变化的未观测到的大集群的生产率冲击也构成重要的潜在的担忧。

第二，城市-研究领域层面未观测到的时变生产率冲击吸引更多的发明家到某个城市的领域中。在回归方程（1）城市和年份的效应不能控制时变的针对城市和特定领域的生产率冲击。

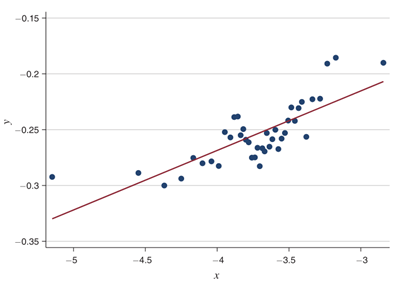
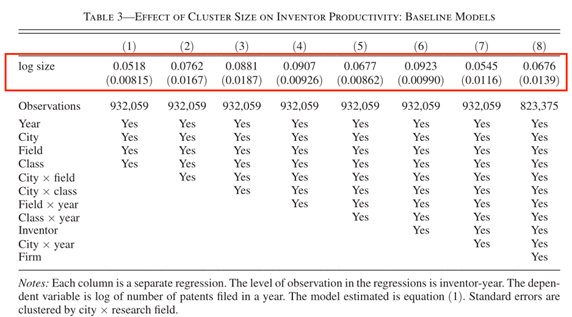
A. 基准估计。 下图为专利数量和集群规模之间的散点图，仅控制年份效应、研究领域效应和城市效应。下图表明，规模大的集群每年会有更高的专利产出。表3列示了方程（1）的回归结果，表3（1）式控制了年份、城市、研究领域、技术类别的固定效应，（2）-（8）依次纳入城市和研究领域、城市和技术类别、研究领域和年份、技术类别和年份、发明家个体、城市和年份、公司个体的固定效应。

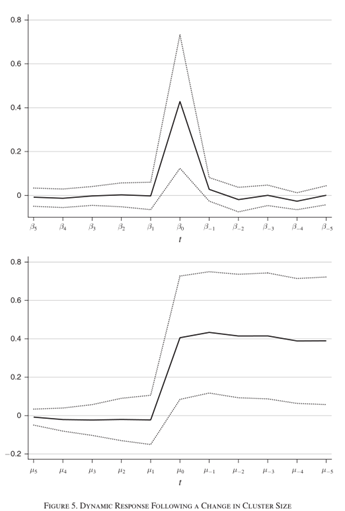
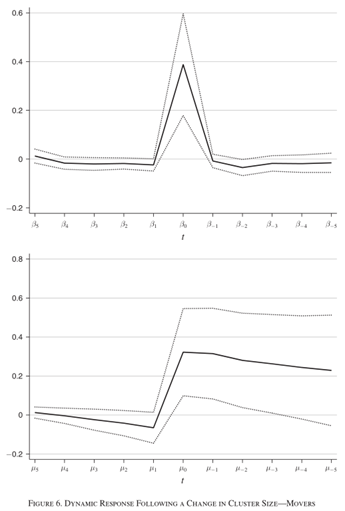
B. 动态响应。 β1至β5提前期的系数可以确定当年发明家生产率如何响应未来规模的变化。β(-5)至β(-1)滞后期的系数可以确定集群大小的变化是如何随时间变化的，尤其是这种影响是短暂的还是永久的。图5和图6具有三个值得关注的特征。第一，β1至β5检验了未来的处理值是否会影响当期的生产率。如果本文的估计反映了一个真实的生产率溢出效应，那么未来集群的规模不会影响当期的生产率，即当期的生产率由当期的集群规模决定；其次，估计显示，在集群规模发生变化的一年中，重点工作人员的生产率会立即提高。生产率的增长速度可能惊人地快；第三，影响深远持久。

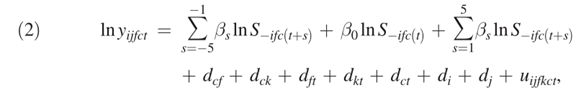
C. 工具变量估计。 在本节中考虑使用2个工具变量，以分离特定和外生的冲击对集群规模的影响。采用工具变量估计可以有效处理联立性问题，即在城市-研究领域层面上可能存在与集群规模变化相关的未观测到的时变生产率冲击。

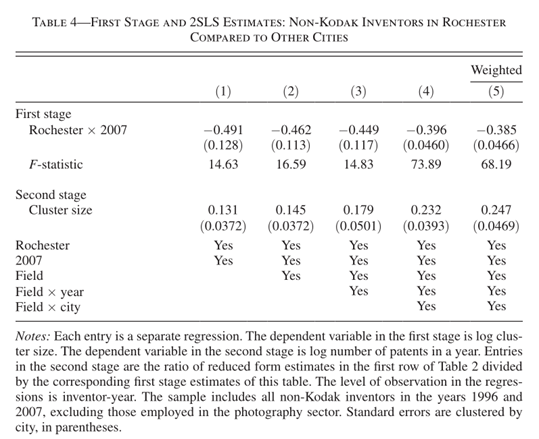
罗彻斯特。工具变量选用罗彻斯特×2007，估计方法为两阶段最小二乘法（2SLS），第一阶段和第二阶段估计如表4所示。

公司的空间网络。下面使用在多个位置公司的地理结构来构建工具变量，以分离来自外部因素引起的本地集群规模的变化。其想法是，随着时间的推移，非重点发明家公司但在重点发明家所在城市和领域存在，在其他城市雇用的发明人数量的变化可以预测当地集群规模的变化，并且不太可能系统地与对重点发明家生产率的未观察到的冲击相关联。

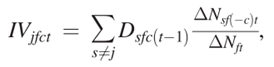
其中，∆Njf(-c)t表示公司j研究领域f第t年，不包括c城市的所有城市发明家的数量，  Dsfc(t-1) 表示若公司s在城市c研究领域年份为t-1年至少有一个发明家取值为1，∆Nft是该领域发明家在全国范围内的变化。除了主要发明家自己的公司外，当地公司在其他城市雇用的发明家数量随着时间的推移而发生变化，从而确定发明家的身份。

工具变量预测的一个局限是仅能关注集群规模改变，而水平无法观测。

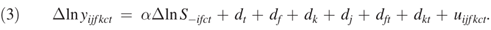
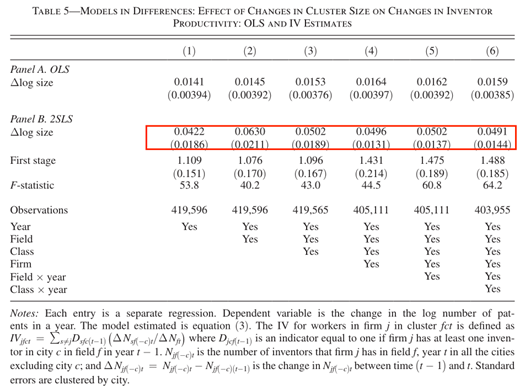
为了验证工具变量的稳健性，使用提前一期工具变量进行估计。其想法是，未来IV的变化所预测的集群规模的未来冲击应该不会对当前时期的生产率或集群规模产生影响。在这两种情况下，我发现统计上不显著的系数，表明IV的未来值不能预测当前集群规模的变化或当前生产率的变化。

05  引用、异质性和稳健性

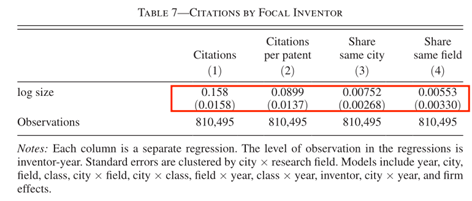
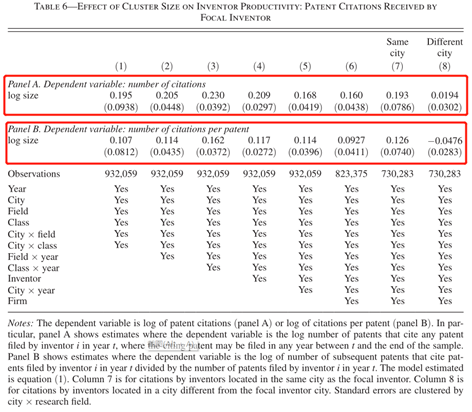
被引和施引。表6面板A和B（1）-（6）分别以专利引用数量和平均每项专利的引用数量为因变量，系数均为正。这表明集群规模不仅可以影响专利产出的数量，也会对专利质量产生影响。（7）和（8）列的因变量分别为重点发明家在同一城市和不同城市的专利引用数量。表7分别以重点发明家的施引数量、每项专利所处领域的平均施引数量、相同城市份额和相同研究领域份额为因变量进行估计。

集群规模、企业生产率和发明家生产率。

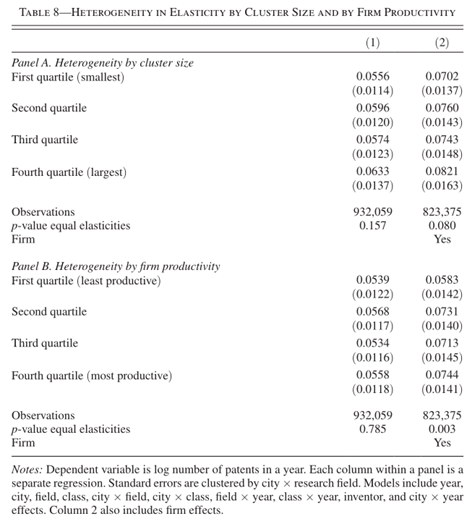
稳健性。

06  集聚对创新总产出的效应

在地理上，发明家倾向于集聚在少数区域，与小集群的发明家相比，在大集群中的发明家拥有更高水平的生产率。因此，一个最为直接的问题是在美国地理集聚对总体的创新产出贡献如何。具体而言，与发明家在各个地区分布更为平均的情况相比，每个领域的发明家集中在少数几个地方，是否会使该国每年产生的专利总数增加？

空间集聚如何影响专利总数量。假定存在两个集群A与B，设集群A的规模大于集群B，专利产出与集群规模之间存在唯一确定的函数关系。考虑一个反事实的情况，即部分发明家从集群A移动到集群B，当两个集群规模相等时，此时A与B的规模为集群总规模的一半。集群总体规模不变，那么A的规模将会减小，而B的规模扩大。变化后的总体的产出水平如下：

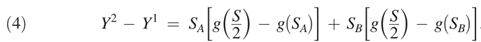
再分配对总产出的影响取决于最初较大的集群中产出损失的大小A和最初较小的集群中产出收益的大小B。式（4）阐明了聚合效应取决于每个集群中发明家的生产率的变化，该变化由初始集群大小加权。直观地说，与最初较小集群的相同变化相比，最初较大集群中发明家生产率的变化对所生产专利总数的总体影响更大。

将式（4）进行推广，得到式子（5）

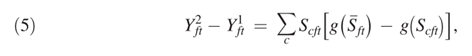
在反事实中，只有集群规模发生变化，而经济中的其他一切都保持不变。事实上，集群大小的变化可能会引起一般均衡效应。

集聚对专利总数的影响估计。

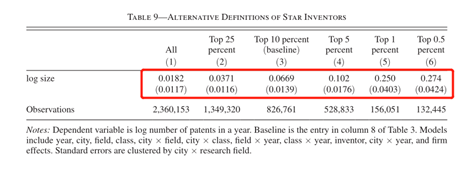
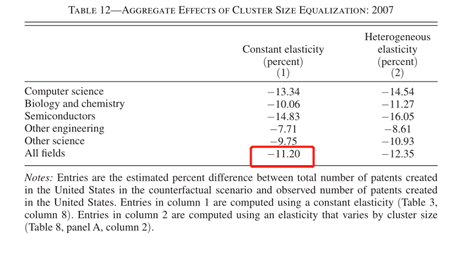
表12第1列按领域列出2007年的估计数。如果计算机科学家均匀分布在各个城市，2007年美国计算机科学专利总数将减少13.34%。生物化学、半导体、其他工程和其他科学领域的损失将是−10.06%，−14.83%，−7.71%，以及−9.75%。最后一行为总体效果。2007年美国专利总数的变化是−11.20%。总的来说，根据表12中的估计，我得出的结论是，在美国，集聚带来的总生产率收益很大。

07  结论

美国经济地理最显著和最重要的方面之一是高科技部门的地理集聚程度。高科技公司和工人集中少数劳动力价格较高的地方，如旧金山、纽约、波士顿和西雅图。2007年，计算机科学、半导体、生物化学领域的前十大集群分别占该领域所有发明家的69.3%、77.0%和59.2%。2007年，这些份额明显高于1971年，这表明发明家的地理集聚在不断增加。研究发现集群大小对发明家的生产率有着重要的经济影响。发明家从一个小群体转移到一个大群体时，年生产率会有所提高，这可以通过一年内产生的专利数量或引用次数来衡量。一年内产生的专利数量相对于集群规模的估计弹性为0.0676（0.0139）。这一估计反映了集群规模对生产率影响的集约边际，但忽略了广延边际。因此，很可能是整体效应的下限。研究发现，美国作为一个整体，从发明家的集聚中获得了总收益。估计表明，与所有集群均相等的反事实情况相比，美国在给定年份创造的专利总数要多出11.20%。高科技部门的集聚可能会加剧社区间收入和收入的不平等。同时，它似乎对美国的整体创新生产非常重要。如果对高科技公司的引入进行适度补贴，需要同时考虑效益和成本。

Abstract

The high-tech sector is increasingly concentrated in a small number of expensive cities, with the top ten cities in "Computer Science", "Semiconductors" and "Biology and Chemistry", accounting for 70%, 79% and 59% of inventors, respectively. Why do inventors tend to locate near other inventors in the same field, despite the higher costs? I use longitudinal data on top inventors based on the universe of US patents 1971 - 2007 to quantify the productivity advantages of Silicon-Valley style clusters and their implications for the overall production of patents in the US. I relate the number of patents produced by an inventor in a year to the size of the local cluster, defined as a city research field. I first study the experience of Rochester NY, whose high-tech cluster declined due to the demise of its main employer, Kodak. Due to the growth of digital photography, Kodak employment collapsed after 1996, resulting in a 49.2% decline in the size of the Rochester high-tech cluster. I test whether the change in cluster size affected the productivity of inventors outside Kodak and the photography sector. I find that between 1996 and 2007 the productivity of non-Kodak inventors in Rochester declined by 20.6% relative to inventors in other cities, conditional on inventor fixed effects. In the second part of the paper, I turn to estimates based on all the data in the sample. I find that when an inventor moves to a larger cluster she experiences significant increases in the number of patents produced and the number of citations received. Conditional on inventor and firm effects, the elasticity of number of patents produced with respect to cluster size is 0.0662 (0.0138). The productivity increase follows the move and there is no evidence of an effect in the years leading up to the move. IV estimates based on the geographical structure of firms with laboratories in multiple cities are statistically similar to OLS estimates. In the final part of the paper, I use the estimated elasticity of productivity with respect to cluster size to quantify the aggregate effects of geographical agglomeration on the overall production of patents in the US. I find macroeconomic benefits of clustering for the US as a whole. In a counterfactual scenario where the quality of U.S. inventors is held constant but their geographical location is changed so that all cities have the same number of inventors in each field, inventor productivity would increase in small clusters and decline in large clusters. On net, the overall number of patents produced in the US in a year would be 11.07% smaller.

推文作者：

翟小清，王丽杰，梁宗红

辽宁师范大学海洋可持续发展研究院硕士研究生

联系邮箱：1907496136@qq.com

欢迎各位老师同学批评指正

声明：推文仅代表文章原作者观点，以及推文作者的评论观点，并不代表香樟经济学术圈公众号平台的观点。