推文人 | 周俊铭

论文信息：Jon Kleinberg, Himabindu Lakkaraju, Jure Leskovec, Jens Ludwig, Sendhil Mullainathan, Human Decisions and Machine Predictions, The Quarterly Journal of Economics, Volume 133, Issue 1, February 2018。

 

合众国的犯罪活动日益猖獗，在纽约这一个城市，年均立案数量就接近30万件。来自芝加哥大学公共政策系的教授联手4位计算机领域的学者，组成“正义联盟”，致力于打击罪恶。不过“武力救不了美国人”，5位学者决定另辟蹊径，用自己的研究来替月行道儆恶惩奸。

 

制度要求法官来决定是否允许嫌疑人保释。5位学者尝试用机器学习的方法，来预测犯罪嫌疑人的保释情况。研究发现，机器学习能够有效地改进法官的保释决策。如果按照算法，给定保释率不变，嫌疑人在保释期间的犯罪率最多可以减少24.7%，或者，给定犯罪率不变，嫌疑人的关押率最多可以减少41.9%。即使考虑一系列内生性的问题，研究的基本结论依然稳健。论文的中心思想概括起来就是，“机你太美”！

 

背景知识

 

根据美国现行制度，嫌疑人被捕后不久，就会进行一次保释聆讯。在聆讯时，法官将决定是否允许嫌疑人保释，如果允许，嫌疑人可以交一笔保证金，来换取直到开庭前的暂时的人身自由，如果不允许，嫌疑人就被继续拘留，直到开庭。

 

实际上，是否允许保释主要基于两点考虑，其一，嫌疑人会不会“细软跑”， 如果保释，开庭时他是否能够正常出席受审，其二，保释期间，嫌疑人会不会重新被捕，即他会不会继续犯罪。论文研究的主要部分只涉及第一点考虑。可供法官参考的信息主要包括：嫌疑人这次被捕所受的指控，嫌疑人以往的犯罪记录，还有嫌疑人的个人信息。

 

数据来源

 

论文使用了2008—2013年间，纽约城超过75万件保释聆讯的案件数据。数据样本提供的信息包括：当次被捕时嫌疑人所受的指控、以往的犯罪记录、以往的“细软跑”记录、嫌疑人的个人信息等。数据样本同样包含了当次保释聆讯的结果，共分为不能保释，保释后正常出庭，保释后“细软跑”，保释期间被捕4种。

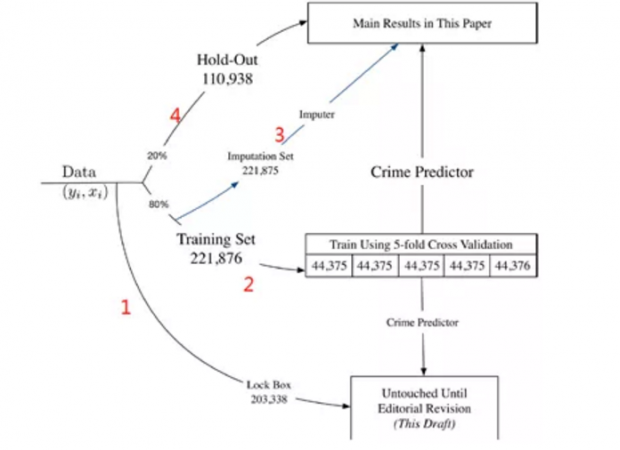
上图表示了数据的使用方法。首先，论文作者预留20万个样本点，向杂志的编辑和审稿人炫耀模型的明察秋毫。（红色数字1）其次，22万个样本点用来训练机器学习的模型。（红色数字2）再者，22万个样本点用来处理缺失值。（红色数字3，用于稳健性检验）最后，11万个样本点用来测试模型。（红色数字4）换言之，论文作者共投入了55万个样本点给机器去学习，才得出了现在我们看到的这个模型。

 

一、写出法官的效用函数

 

为了形式化表达，在开始机器学习的步骤之前，论文作者要先写出法官的效用函数。

 

以上是法官j对每一次保释聆讯的效用函数。y表示获保释的嫌疑人“细软跑”的概率，01二值变量R表示法官的决定，允许保释则取1。

 

等号右边第一项表示，获保释的嫌疑人“细软跑”所带来的负效用，第二项表示，不允许保释，继续关押嫌疑人所带来的负效用。参数ab的取值均为正。可见，效用函数反映了法官对保释决定的权衡，如果允许保释，嫌疑人可能“细软跑”甚至趁机犯罪，如果不允许，关押也要消耗成本。

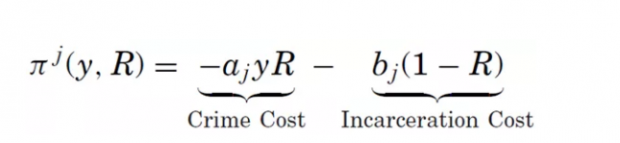
y：保释期间嫌疑人“细软跑”的概率，取值1表示“细软跑”，获得保释却不出庭，否则取值0。注意，这个取值只对获得保释的嫌疑人有意义。

 

x：可以观测并记录的案件信息。

 

z：法官可以而论文作者不能观测的案件信息，例如嫌疑人被捕时的衣着是否得体。这些信息会影响法官的主观决定，但不会被记录，因此对论文作者来说是不能观测的。

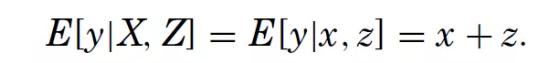
以上是法官j的决策函数，我们可以理解成，这是对R的估计。给定一次保释聆讯，当且仅当关于案件信息的函数h小于某个门槛值时，法官j会决定允许保释。

 

在这里，论文作者想通过机器学习，找出一种不同于法官j的决策函数的算法（上标d表示），算法对应的效用函数满足下式

R的上划线表示加总，是法官j所处理的全部聆讯案件的允许保释率。受数据限制，论文作者设等号右边第二项为零，即保持算法得出的允许保释率和法官决策的相同，从而两者效用的差异仅来自对于“细软跑”概率的估计，展开后可见，估计差异来自两方面：法官允许而算法不允许保释，或者反之，法官不允许而算法允许保释，如下式。

论文作者只能测量前者，毕竟法官可以而论文作者不能观测的案件信息是存在的（变量z）。不过，论文作者称，所用的计量策略已经在一定程度应对了这种情况。接下来，我们打开随身携带的折凳，默默地围观。

 

二、机器学习似乎有用武之地

 

尽管存在着上述的估计问题，但在这部分，论文作者还是展示了机器学习的威力。下图的横轴是算法预测的“细软跑”概率，纵轴是实际的允许保释率。

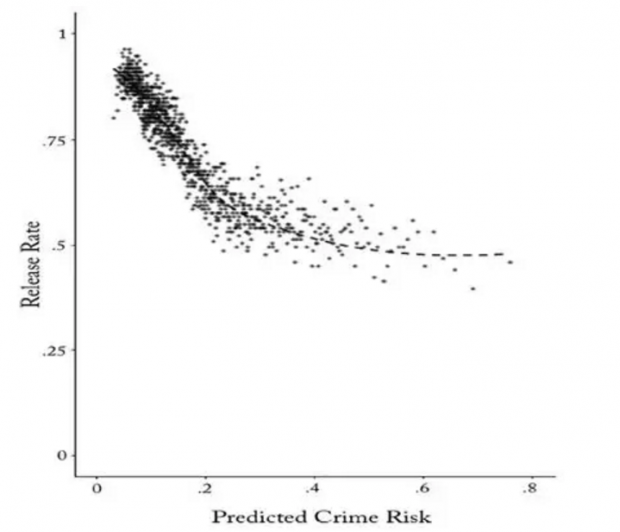
这幅图告诉我们两个信息：（1）法官和机器的决策的确有不同之处，集中在图右的高风险区域，就是说，处理更可能“细软跑”的嫌疑人，法官和机器的分歧明显，似乎这正是机器学习的用武之地了。（2）法官可以而论文作者不能观测的案件信息（变量z）的确影响了法官的决定，否则的话，我们应该看到呈现阶梯式的图像，“细软跑”风险低于某个门槛值就允许保释，高于某个门槛值就不允许保释。

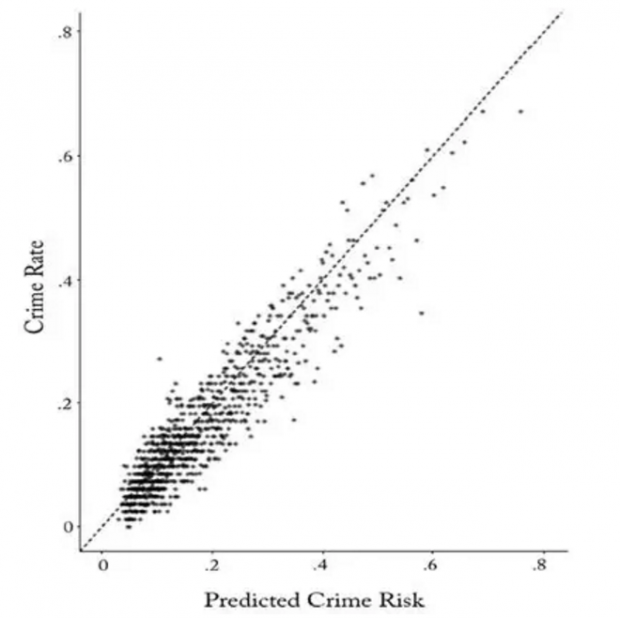
上图的纵轴是获得保释的嫌疑人的实际“细软跑”率。可以看出，法官和机器在此达成一致了，法官可以而论文作者不能观测的案件信息（变量z）在此没有什么影响。

 

当涉及到对概率变量作预测时，计量经济学的一般做法是 logit 回归。所以，下表同时报告了机器学习和 logit 回归的预测结果。机器学习不落下风，在处理高风险子样本时尤其具优势（第1行）。

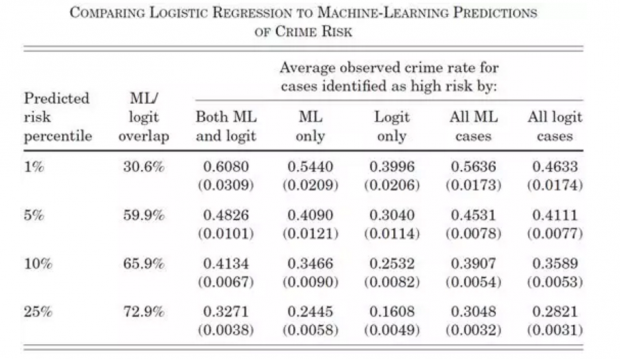
三、机器学习能够改进法官判案的效果

 

迄今为止，我们看见了机器学习在获保释嫌疑人的子样本中的良好表现。接下来，论文作者想把机器学习推广到不允许保释的嫌疑人，但变量z（法官可以而论文作者不能观测的案件信息）的处理，成为了摆在眼前的难题。

 

首先，样本的案件数据同样包含了法官的信息，论文作者就用 permutation test 来说明，法官和嫌疑人之间的匹配是没有相关性的。

 

此外，尽管不同的法官有着不同的允许保释率，但这种高低差异并非来自对于变量z的利用技术，就是说，面对相同的z，不同的法官也会作出相同的决定。下图显示了这一点。按允许保释率的从高到低，把法官分入5等份组别，给定可以观测的案件信息之后，对应的案件中，获保释嫌疑人的“细软跑”概率呈现出相同的 pattern。

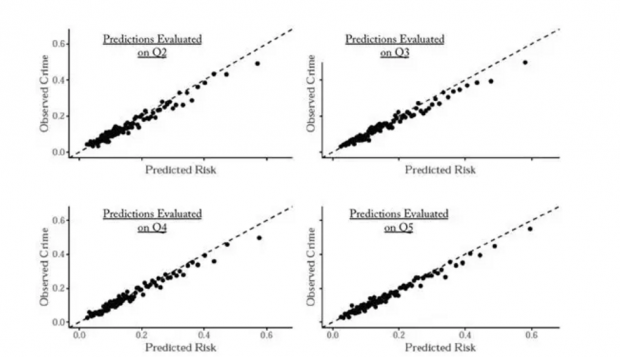
然后，论文作者以允许保释率最高的法官组别来建立 benchmark，分析机器学习能否改进其他4个组别的法官决策。直观地理解，benchmark 组别包含了关于变量z和法官如何用来决策的信息，因此机器学习所报告的预测结果是相对于 benchmark 而言，就处理了变量z的问题。

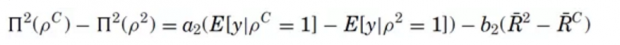
由法官决策函数，改进可能来自两方面：获保释人数不变而“细软跑”人数减少（参数a的项），或者，“细软跑”人数不变而获保释人数增加（参数b的项）。上标c表示算法组别，上标2表示其他组别（除了 benchmark）。结果如下图，横轴表示允许保释率的从低到高，纵轴表示“细软跑”人数的从少到多。5个圆点对应5个法官的组别，最右点是允许保释率最高的 benchmark 组别。

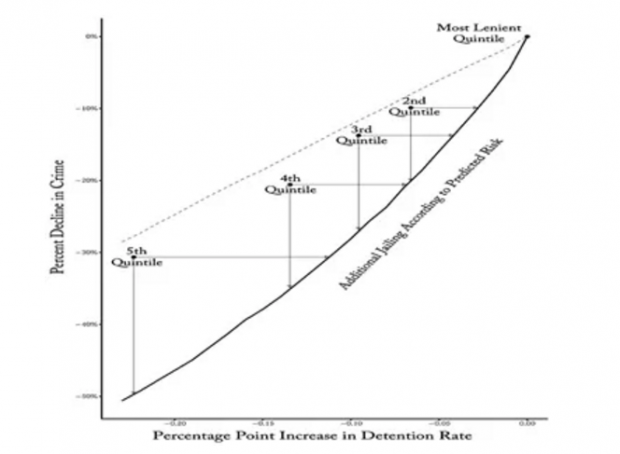
论文作者用最右点的 benchmark 组别，通过机器学习得出一种算法，再把算法应用到其他4个组别，得出倾斜的实线，这条线位于4个圆点的右下方，意味着算法能够改进其他4个组别的法官决策，实现“细软跑”人数的减少，或者是获保释人数的增加。具体的改进数量如下表。

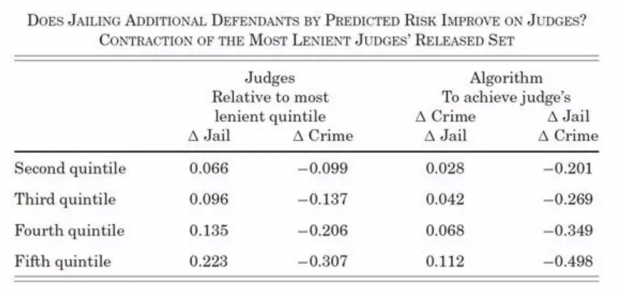
四、完全由机器学习来判案

 

最后，论文作者模拟了完全由算法来决定允许保释与否的情况，如下表

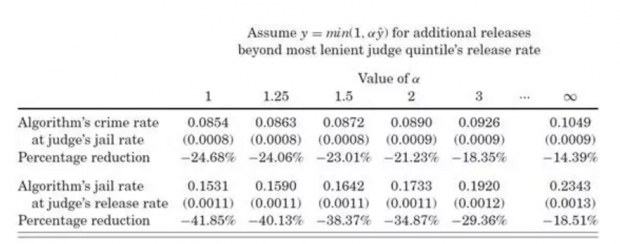
继续用允许保释率最高的法官组别的数据，论文作者估计了一些参数，代入算法，再用算法估计其余的子样本。第1行反映了，保持允许保释率（法官的判决）不变，算法能够减少获保释后“细软跑”的人数。第2行反映了，保持“细软跑”人数（法官允许保释后）不变，算法能够减少关押的人数。第1列就是论文的主要结论，按照算法，保持允许保释率不变，嫌疑人在保释期间的“细软跑”率最多可以减少24.7%，或者，保持“细软跑”率不变，嫌疑人的关押率最多可以减少41.9%。

 

稳健性

 

论文作者回应了三个主要的 argument，以确保结论的稳健。

 

第一，在保释聆讯，法官的决定可能不仅考虑嫌疑人会不会“细软跑”，还要考虑嫌疑人会不会趁保释期间去犯罪，尤其是犯重罪。如果机器学习只是预测“细软跑”的概率，算法对法官决策的改进作用就不一定可靠了。

 

样本包含了嫌疑人在保释期再次被捕的有关数据，论文作者据此做了检验，结果显示机器学习预测的“细软跑”和再次被捕是相关的。因此，尽管算法只考虑“细软跑”的概率预测，它还是能够改进法官的决策。

 

第二个argument 关于种族平等，其中逻辑和第一个的类似。论文检验的结果是，即使法官需要考虑种族平等的政治正确，机器学习还是创造了改进的空间。同样地操作，论文作者发现，第三个关于嫌疑人的就业状态和家庭环境的 argument 也会不削弱结论的稳健。

 

附录：论文所用的机器学习方法是 gradient boosted decision trees，这个网页有一个简单通俗的介绍。https://machinelearningmastery.com/gentle-introduction-gradient-boosting-algorithm-machine-learning/

 

Abstract

 

Can machine learning improve human decision making? Bail decisions provide a good test case. Millions of times each year, judges make jail-or-release decisions that hinge on a prediction of what a defendant would do if released. The concreteness of the prediction task combined with the volume of data available makes this a promising machine-learning application. Yet comparing the algorithm to judges proves complicated. First, the available data are generated by prior judge decisions. We only observe crime outcomes for released defendants, not for those judges detained. This makes it hard to evaluate counterfactual decision rules based on algorithmic predictions. Second, judges may have a broader set of preferences than the variable the algorithm predicts; for instance, judges may care specifically about violent crimes or about racial inequities. We deal with these problems using different econometric strategies, such as quasi-random assignment of cases to judges. Even accounting for these concerns, our results suggest potentially large welfare gains: one policy simulation shows crime reductions up to 24.7% with no change in jailing rates, or jailing rate reductions up to 41.9% with no increase in crime rates. Moreover, all categories of crime, including violent crimes, show reductions; these gains can be achieved while simultaneously reducing racial disparities. These results suggest that while machine learning can be valuable, realizing this value requires integrating these tools into an economic framework: being clear about the link between predictions and decisions; specifying the scope of payoff functions; and constructing unbiased decision counterfactuals.