1、引言

程序偏向型的技术变迁（Routine-Biased Technological Change）带来分析性和手工承担的就业增加，程序性任务的就业减少。承担分析性任务的工人，除了有适应新技术的比较优势，更从分析性任务中获得更高的工资回报。根据Acemoglu and Autor（2011），任务是指为了生产特定产品所进行的生产活动的一个单元，而技能是指工人的受教育程度。

如果考虑经济活动的分布，分析性任务和技术变迁的互补会使承担程序性任务工人陷入更加不利的处境。这是因为就业密度高的地区有更加专业化、高技能的工人，提供了相对更少的程序性工作。我们的分析表明在荷兰就业密度和工作的程序化任务强度成反比。在我们的分析中，程序化程度最低的职业像职业经理人和教授，承担了分析性任务，包括数据分析、创造性思考，信息解译，复杂的人际沟通。相比之下，那些程序性任务密集的职业需要完成重复性、常规性任务，比如汽车、洗衣店工人或者纺织机器操作员。

为什么需要分析性任务的职业和企业会集中在就业密度高的城市地区？一是工人的自选择，Combes et al.(2008)的研究表明空间工资差异的一大部分可以由工人特征来解释；二是更有创造力的企业家和公司的自选择；三是集聚效应会促进新想法产生和资源互补，使得大城市的职业任务类型更加多元化，程序性任务更少。

工作任务的程序性程度会影响集聚经济。我们假设城市对那些分析性任务密集的工作提供更高工资和更好的就业机会。具体来说，城市工资溢价在不同的工作任务程序化指数上应该存在异质性。这是因为对于非程序性任务密集的工作学习速度更快，匹配更好。

本文的研究发现，在控制了自选择和缓解内生性问题后，就业密度对工作的程序性任务强度具有显著的负向影响，也就是说集聚经济会减少工作的程序性任务强度，将更多复杂性任务集中在就业密度高的地区，这与文献中讨论的“城市是新想法和创新的荟萃之地”相一致。此外，工作任务的复杂性程度不同，城市工资溢价程度也不同。例如，对于从事非程序性工作的工人来说，工资-密度弹性为0.15，而这一弹性对于从事程序性工作的人来说几乎为0。此外，无论工人的受教育程度如何，可观测特征类似的工人承担分析性任务会得到更高的城市工资溢价，这表明仅使用技能来解释工资溢价是不合适的。本文为技能与工作匹配以及城市提供更好的学习机会两个潜在机制提供了启发性证据。

2、研究框架

2.1. 数据和变量

（1）数据

本文的估计基于2006-2016年间的LEED数据。LEED数据包括：①荷兰劳动力调查数据（Labour Force Surveys）是核心，提供雇员的受教育程度和职业两个指标；②税务登记（Tax Registers），包含雇主特征、雇员年收入、工作期限和每个雇员在工作期限内的工作天数。这个数据包含了每个工作唯一识别码，是工作、雇员和工作期限的组合，利用这个唯一识别码可以匹配LFS数据；③父代-子代关联的数据集（Kindoudertab），提供荷兰所有孩子和他们的法律父母的信息。

（2）指标构建

①职业的程序性任务强度指标（Routine Task Intensity，后文均简称为RTI）。将Autor and Dorn(2013)用到的SOC调整到荷兰职业的最高精度的4分位ISCO，这一调整可以在职业分解到最低水平时测定任务程序性程度。SOC与ISCO的转换是由美国劳工调查局完成，可以与荷兰LFS数据中的职业进行很好的匹配。工作任务的程序性程度是根据O*NET数据库的重要性得分来量化，程序性程度由高到低可以分为routine cognitive(RC)，routine manual(RM), non-routine manual(NRM), non-routine analytic(NRA)和non-routine interactive(NRI)，假设一个职业o在t年的程序性任务强度Rot为,

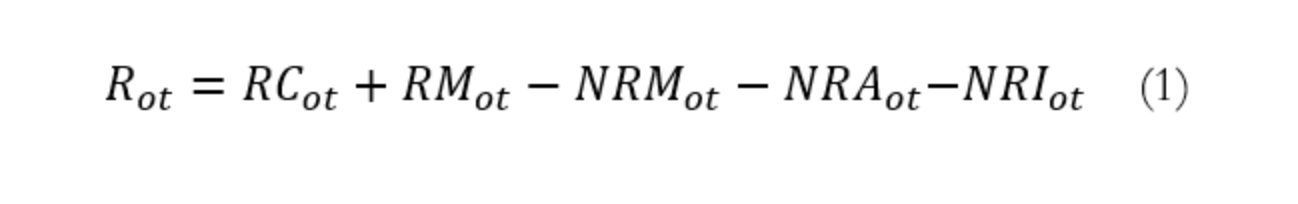
为了减少数据的维度，这五个指标(4分位ISCO)合并成一个综合指标RTI，RTI经过标准化处理。

②潜在工作可获得性（potential accessibility to jobs）

这一指标构建有多个数据来源。首先，我们使用VUGeoPlaza 数据库中4033个荷兰街区汽车通勤时间信息，匹配街区层面4位邮编代码区位，计算根据通勤时间加权的特定地理距离内的工人数量。

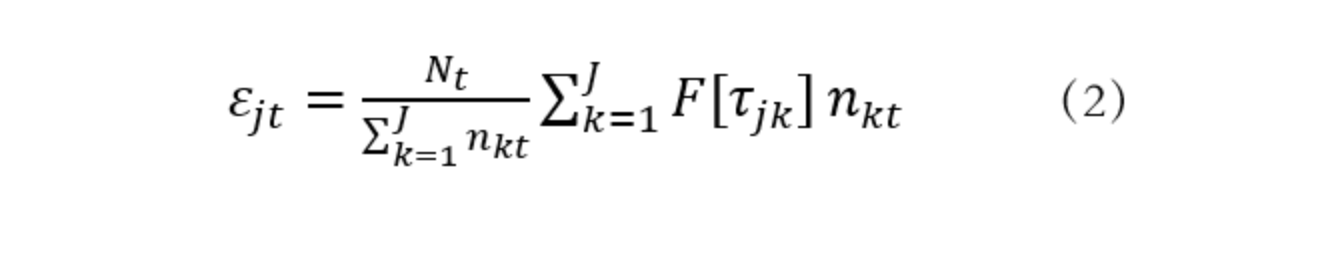
其中，Ɛjt 是 j 地 t 年根据通勤时间加权的工人数量，τjk 是家庭所在地 j 和工作地k=1,…, J的通勤时间，F[τjk ] 是通勤时间至少在τjk 分钟的工人数量占比，nkt 是LFS数据中k地的工人数量，Nt 是荷兰总的就业人数。这一指标的好处是给定家庭所在地到工作地的通勤时间和路网反映工人实际可获得工作数量，消除了由于任意选择空间单元带来的方法问题(Briant et al., 2010)。

另外，根据1909年普查数据也构造了历史上潜在工作可获得性指标作为本文的工具变量。对于1909年的1121个城市，我们观察到1571个职业类型的工人，分为学徒和熟练工两类。对于每一类职业，我们根据LFS匹配需要的受教育水平。另外，还用到了Knol et al.(2004)中的建成区面积和1909年普查数据中市级层面的就业数据。根据Gaigné et al.(2017)提供的1900年铁路网数据，计算了给定通勤时间累积分布的可得的工作数量：

2.2. 描述性统计分析

图1给出了2006-2016年间473，322个观测样本的RTI分布情况，发现异常值较少，RTI<-1对应于需要较高分析性和认知性任务的职业。RTI与分析型任务强度指数的相关性是-0.89，与非程序性手工任务强度的相关性是0.3，与程序性任务强度的相关性是0.7。

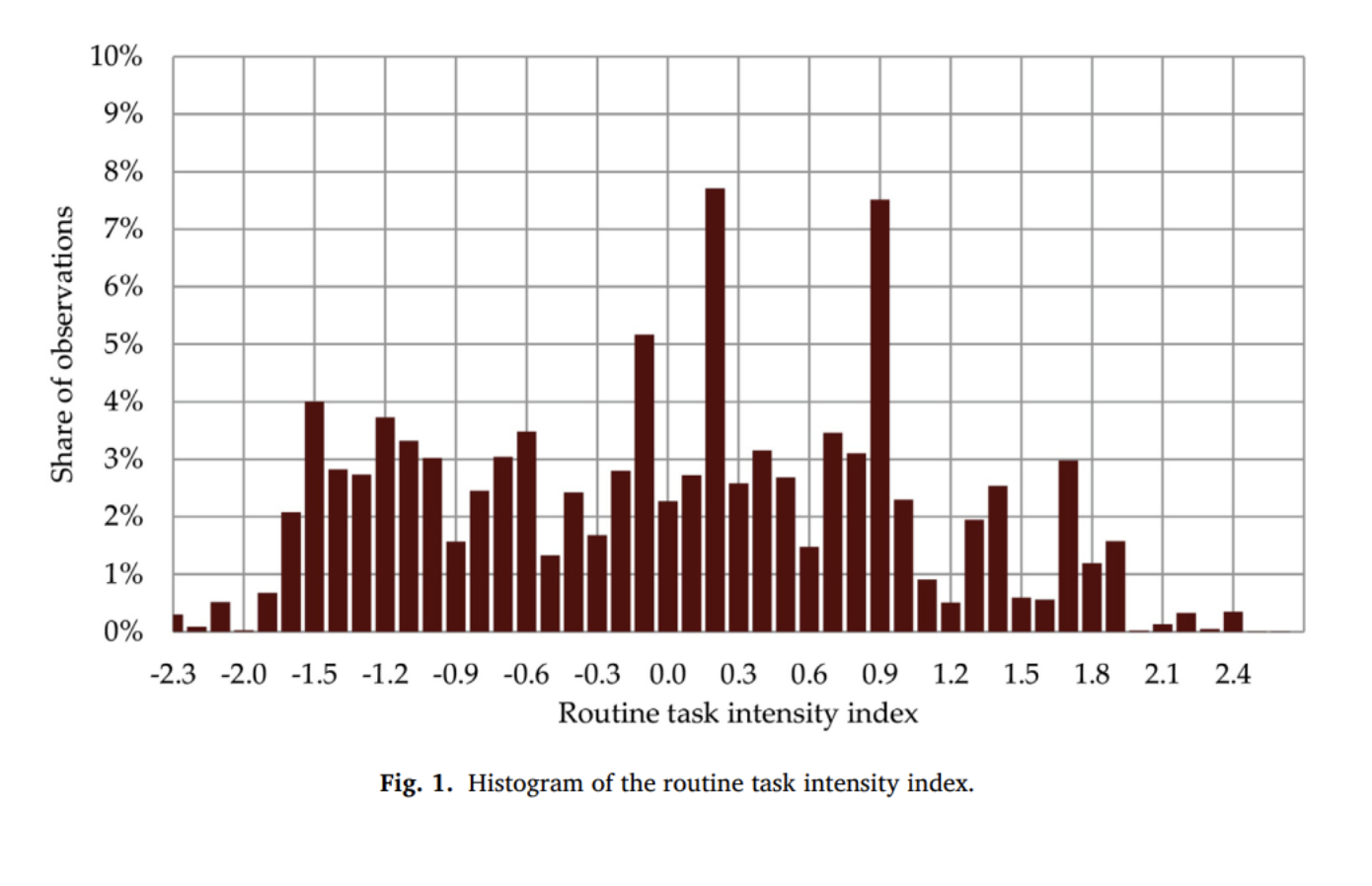
进一步，图2还展示了RTI在不同技能组的分布，发现不管技能水平如何，工人都会承担各种类型的程序性任务。对于初级和低技能工人，许多工作都是程序性任务密集的，只有很少的工作RTI<-1。高技能工人更多集中在非程序性任务密集的工作。

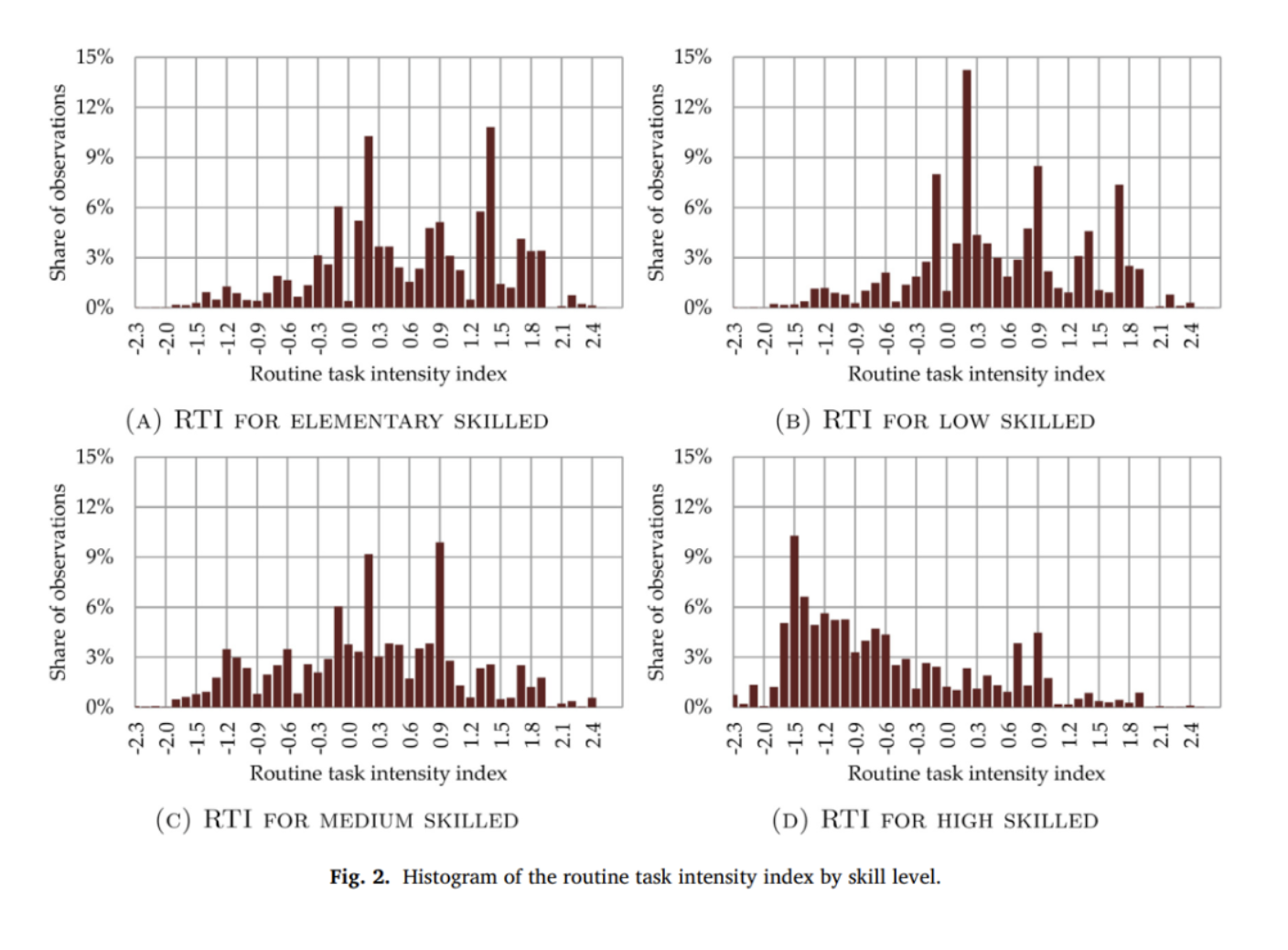
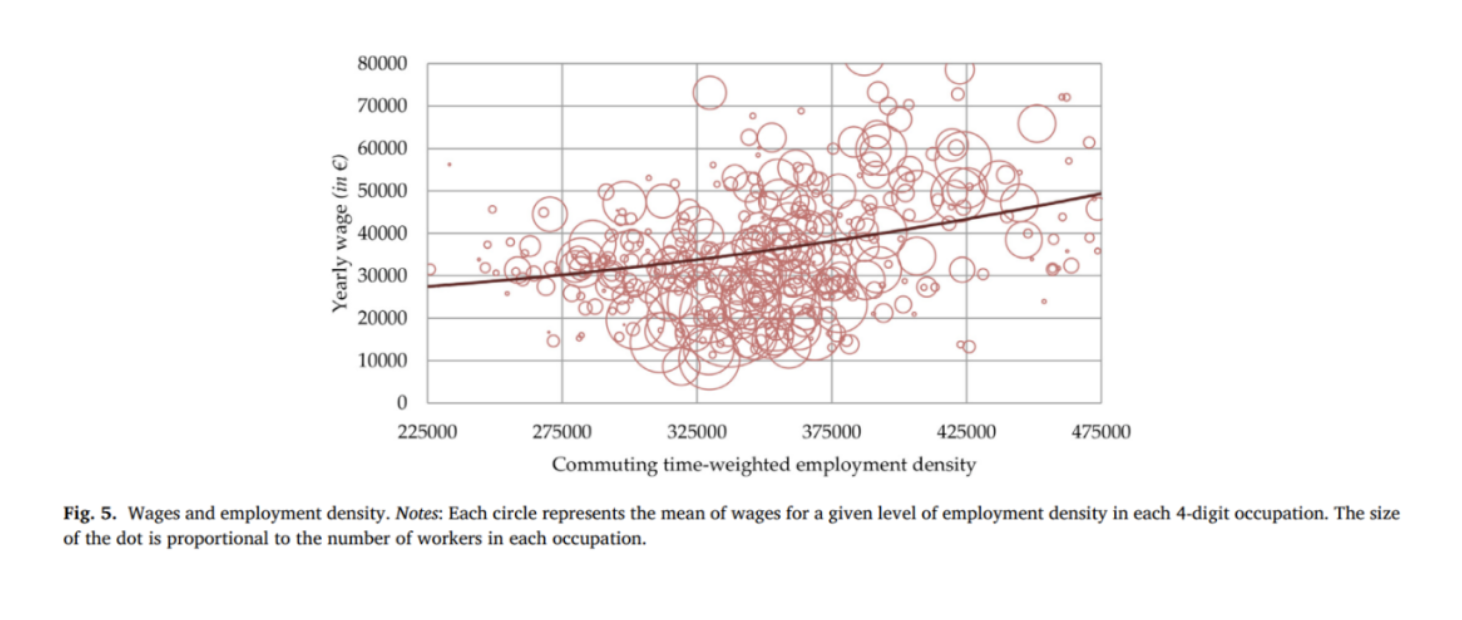
图3反映了荷兰劳动力市场上非程序性任务密集型职业的变化趋势。在2000年，非程序性任务密集工作的占比为0.43，到了2016年增加到0.48。

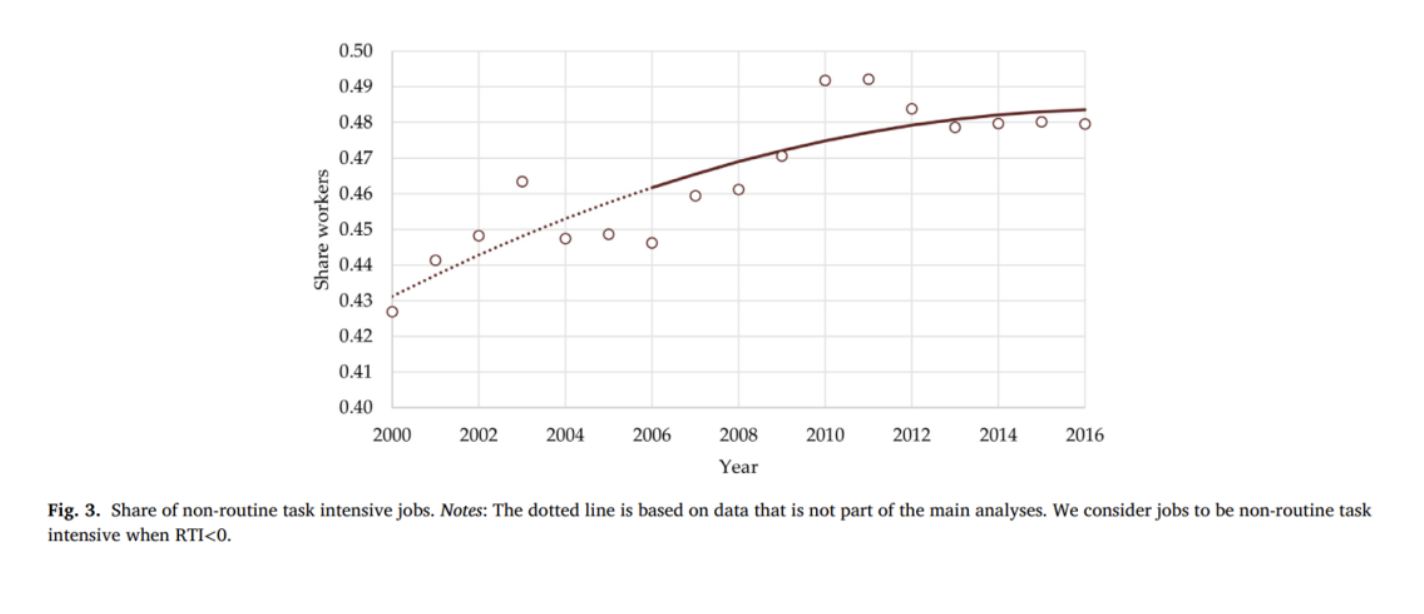
图4反映了根据通勤时间加权的就业密度与RTI之间的负相关关系，表明就业密度高的地区的工作有更少的程序性任务强度。

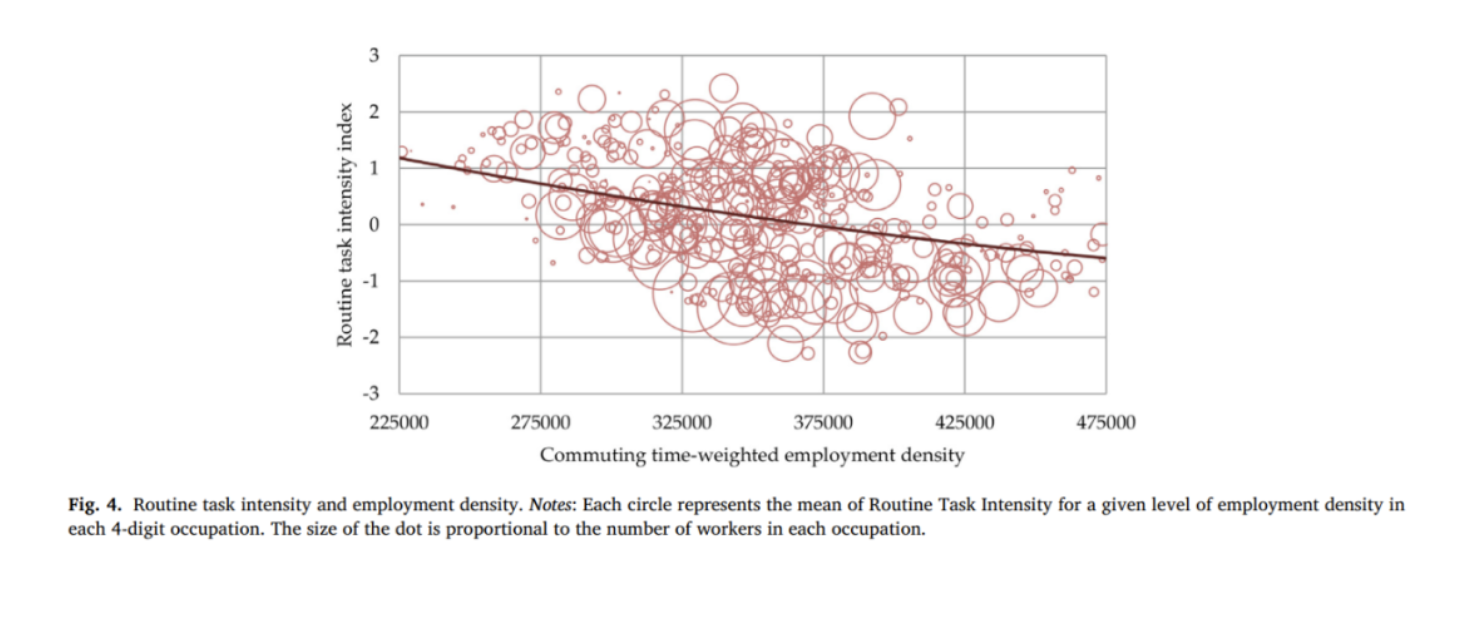
图5反映了根据通勤成本加权的就业密度与年均工资之间的正相关关系，表明就业密度高的地区，工人的平均工资水平也更高。

2.3 计量模型和识别

2.3.1 参数估计：就业密度的作用

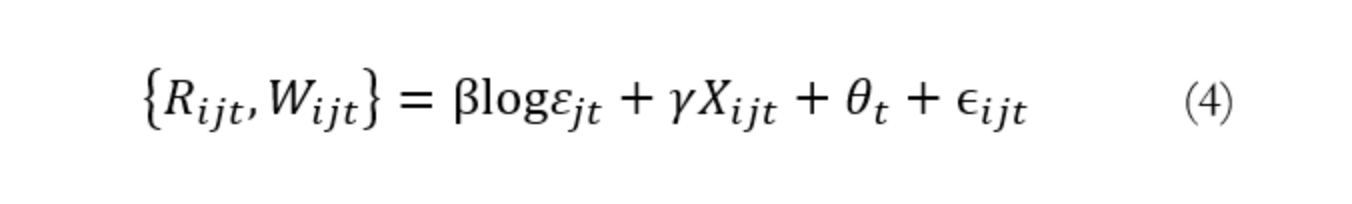
我们观察到t年居住在j地的工人i，本文有两个被解释变量，Rijt 表示任务程序性程度指数，Wijt 表示年度工资的对数，Ɛjt 表示一个工人在离家特定的通勤时间内的工作数量，Xijt表示工人、工作地和居住地的特征，θt 表示年度固定效应。

为了得到β的准确估计，需要解决一系列内生性问题。首先是遗漏变量问题，消费舒适度会吸引高技能劳动者，同时高技能劳动者会获得高工资（Gaigné et al., 2017）。此外，也有可能会遗漏某些不可观测的区位禀赋，例如，某些区域性政策既影响就业密度又影响因变量。第三个内生性问题是反向因果，高生产力的工人和企业会自选择进入就业密度更高的地区（Behrens et al., 2014）。

为了缓解内生性问题，首先加入了一系列控制变量Xijt，包括工人、街区和居住区位的历史特征。工人的特征包括受教育水平、年龄、性别、家庭规模和构成、婚姻状况以及是否在国外出生。加入工人特征可以控制特定工人的自选择效应。工作特征，像工作日数量、工作期限和企业规模等来控制工人的工作类型。所有的回归都包含行业固定效应njea以控制不同区域的劳动力技能差异。在工资的回归方程中还加入了Rijt  以控制RTI产生的任务溢价。我们得到新的回归方程为：

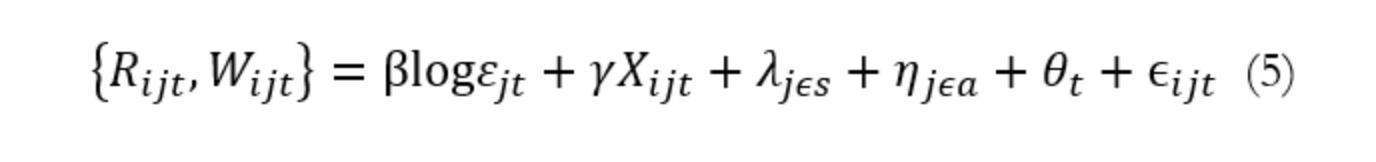
为了更好地解决内生性问题，本文使用1909年历史的就业密度Ɛj1909 作为目前就业密度的IV。背后的逻辑是不可观测的区位冲击不可能跟一个世纪后的被解释变量相关，同时就业密度又有很强的自相关性。

本文在模型设定上并未加入工人个体固定效应，主要是考虑识别来自于居住地发生改变的工人，而这部分人在总体中并不随机（Groot et al., 2014），另外，本文的主要数据来源是LFS，该数据中仅有少量工人可以进行跨期追踪构建面板，更少一部分改变居住地。因此，本文使用其他方式来解决自选择偏差问题。使用1909年就业密度作为当期就业密度的IV，主要的挑战是1909年的就业密度与历史上的工人自选择相关，进而影响当期的工人自选择。本文的处理方式是加入1909年特定通勤时间内的高技能、中等技能、低技能和初级技能工人占比作为控制变量。

此外，为了更好地消除不可观测的能力带来的估计偏差，本文还使用整个荷兰的父代-子代关联数据。这个数据集可以将样本中的每位工人与他们的法律上父母匹配起来，研究具有相同基因特征的双胞胎样本。这一方法的优势是基于居住在不同就业密度地区的双胞胎样本来探讨就业密度和工资之间的关系。

2.3.2 半参数回归

本文的主要兴趣是检验就业密度对工资的影响在不同的RTI水平上会有所差异。我们假定在低水平RTI上的工作更有可能从集聚经济中获益，转化成更高的工资溢价和更好的技能匹配。半参数的回归模型如下，

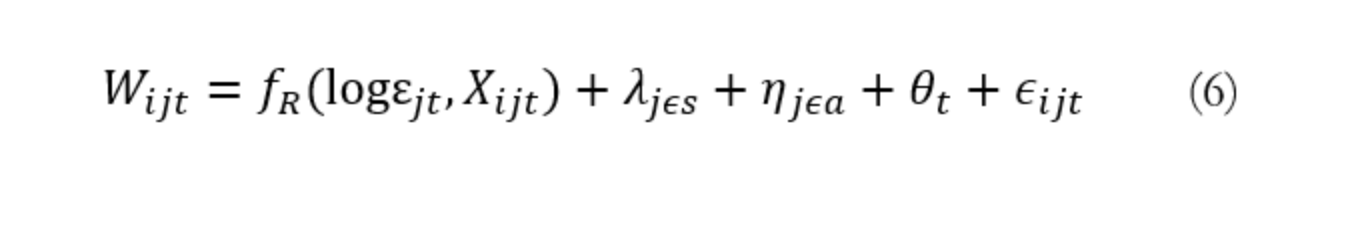
其中，fR(.) 表示就业密度对数和控制变量是RTI的函数，具体设定为

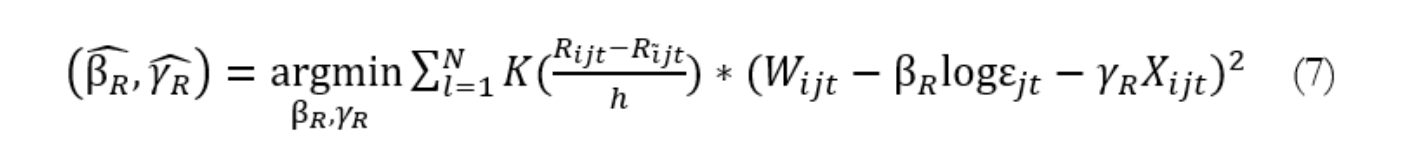
本文使用核密度函数来估计回归系数，

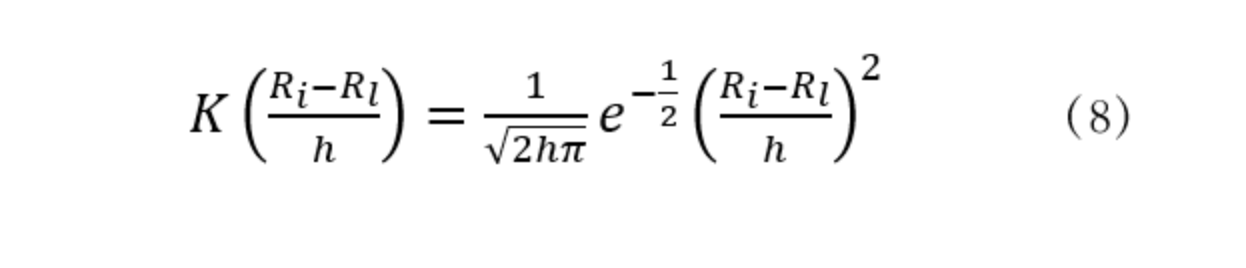
3、回归结果

3.1 就业密度对RTI的影响

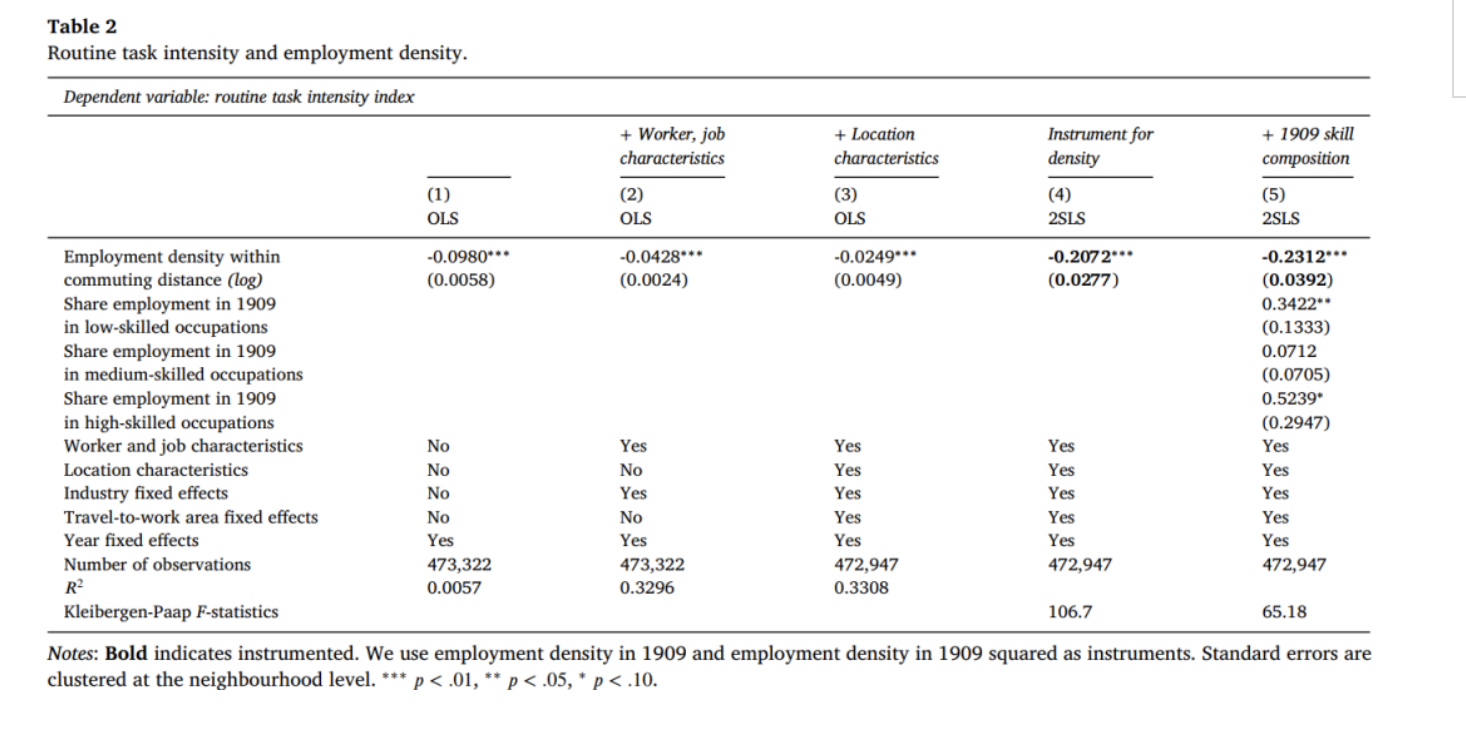
我们假设集聚经济可以促进新想法的产生和创新，创造包含更少程序性任务的工作。因此，预期就业密度与RTI负相关。表2第（1）列是将RTI对就业密度和年份回归的结果，发现就业密度翻倍会带来RTI 0.068个标准差的下降。那么，这一结果是由集聚效应还是能力强的工人和特定类型的职业自选择进入就业密度更高的地区造成的呢？表2第（2）列加入了一系列工人特征、工作特征和行业固定效应，发现回归系数下降了近一半，但是依然负向显著。第（3）列又进一步加入了区位控制变量，在控制舒适度和自选择效应的同时，识别同一劳动力市场内部的就业密度效应，发现当就业密度增加一倍时，RTI下降0.017个标准差。为了解决当期就业密度与区位禀赋和自选择相关从而不能干净地捕捉集聚经济对RTI影响的问题，本文使用1909年就业密度作为工具变量，第一阶段K-P F值很大，说明工具变量具有很强的相关性。第二阶段的系数相比于OLS回归也更大，当就业密度翻倍时，RTI会下降0.16个标准差。使用1909年就业密度作为IV可能存在的问题是1909年的就业密度与当期的自选择相关，历史上就业密度高的地区持续吸引更多高技能和高能力的人。因此，为了解决这一问题，本文计算了1909年高技能、中等技能、低技能和初级技能工人占比作为控制变量，第（5）列结果显示，就业密度对RTI的影响比第（4）列稍大。总体来说，集聚经济与技术进步互为补充，本文的发现是合理的。

3.2 就业密度对工资的影响

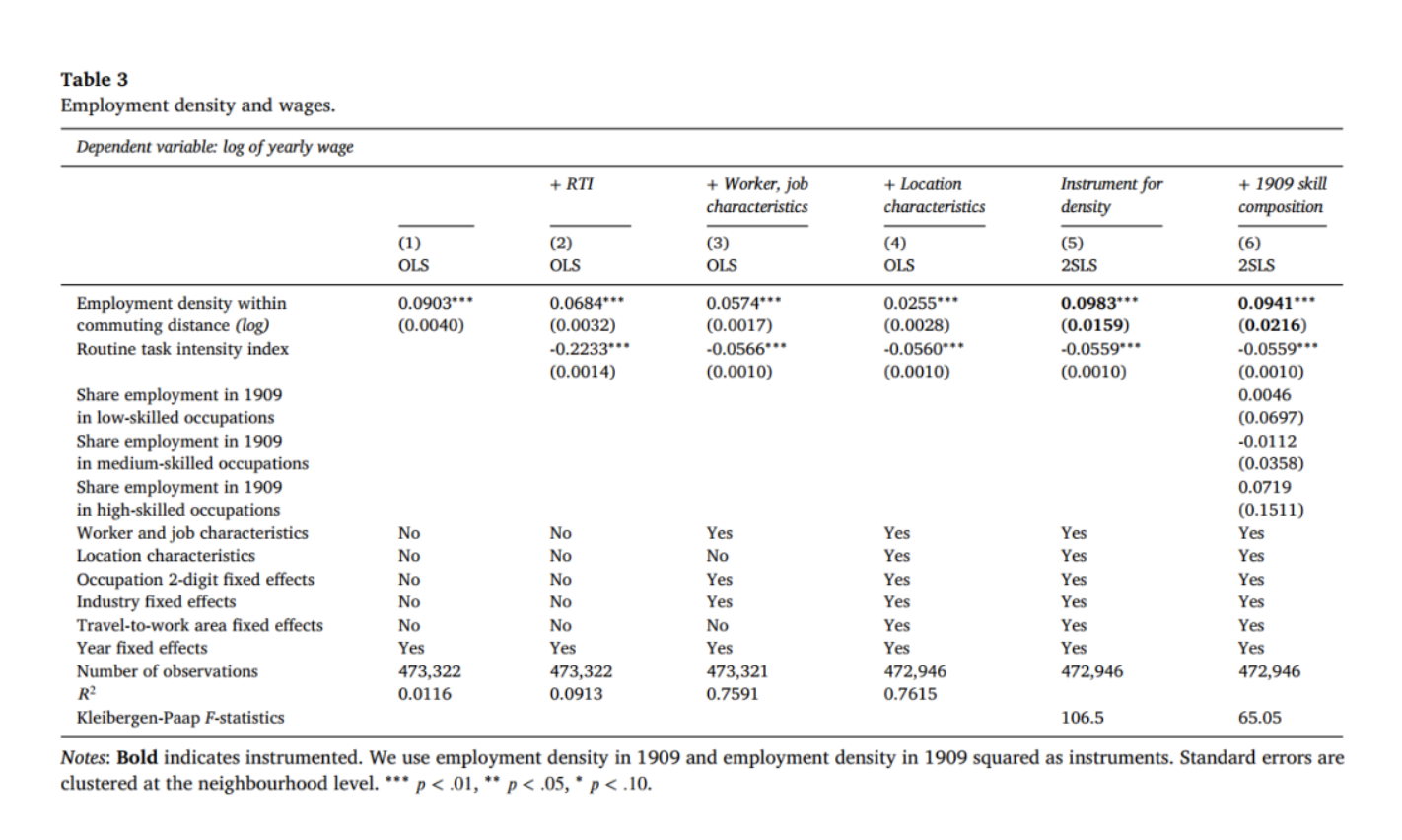
表3第（1）列仅控制了年份固定效应，发现工资对就业密度的弹性为0.09，第（2）列控制了RTI来捕捉高就业密度地区的非程序性任务职业的选择效应，发现就业密度对工资的影响略微下降，RTI对工资的影响为负。第（3）列进一步加入了一系列工人特征、工作特征和行业固定效应，对估计弹性没有太大影响。但是，当控制区位特征时，就业密度对工资的影响系数显著降低，当就业密度翻倍时，工资提升2.5%。第（5）列和第（6）列展示了IV的回归结果。RTI对工资的影响在不同回归模型设定中是相似的，第（4）列加入区位控制变量的回归结果显示，RTI每增加1个标准差，工资会下降5.6%，表明就业密度高的地区不但提供高工资，并且从事非程序性任务密集职业的工人可以获得任务溢价。

3.3 RTI与集聚经济

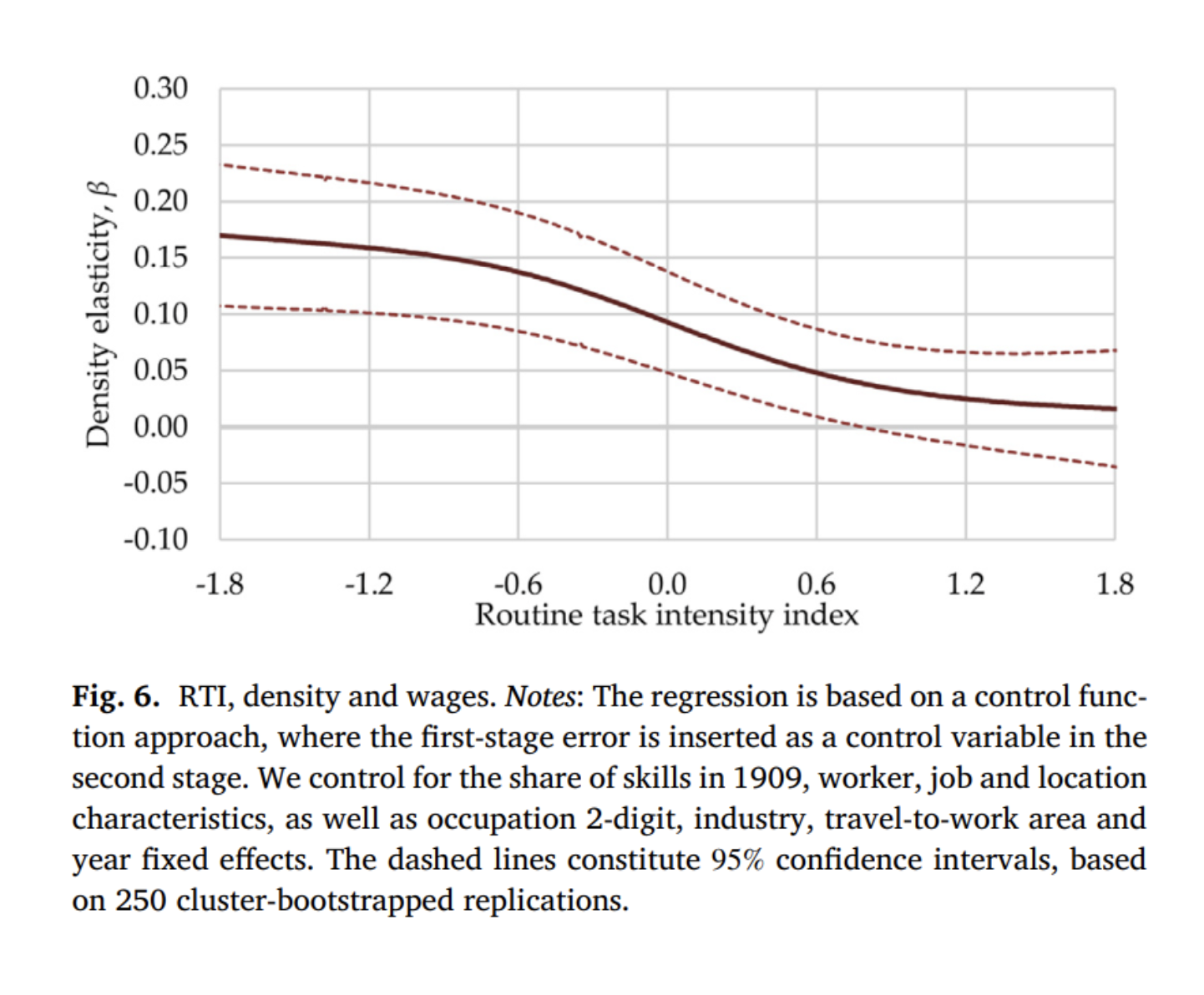
上述结果给出了平均RTI下的就业密度对工资回报的影响，但是我们并不清楚这些回报如何随RTI变化。根据2.3.2 介绍的半参数估计方法，我们得到了不同水平的RTI上工资对就业密度的弹性 βR，如图6所示，发现工资对于就业密度的弹性在统计上显著只对于较低水平的RTI成立，也就是说从事非程序性任务密集职业（包含NRA和NRM任务的职业）的工人可以享受就业密度高地区的工资溢价。

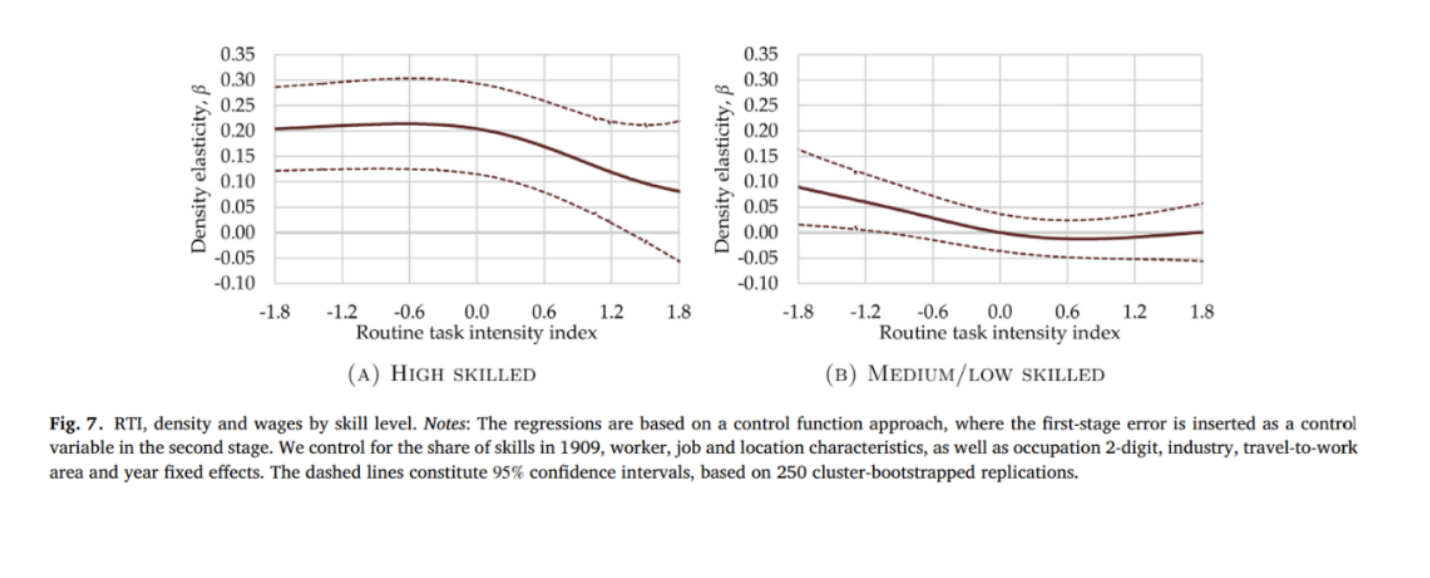
分析性工作（RTI比较低）的集聚效应可能是不真实的，因为大部分的分析性工作是高技能劳动者承担。为了解决这个担忧，图7给出了根据技能分组的工资弹性对RTI估计系数变化趋势图，发现无论是对于高技能还是中低技能工人，如果从事非程度性工作，都能从集聚经济中获益，但是对于承担程序性任务的低技能工人来说，这一效应下降更快。这些结果表明只有低RTI工人可以从集聚经济中获益得到高工资，并且对于高技能和中低技能的工人都存在，说明集聚经济的异质性回报不只是通过技能，也可以通过任务类型来解释。

4、机制探讨

本部分用来解释为什么集聚经济仅存在于承担非程序性任务密集工作的工人（图6）。我们使用与已有文献类似的匹配和学习机制代理变量来探讨两条机制是否可以解释工资-密度弹性在不同RTI之间的差异。由于受到微观数据可得性的限制，本文提供的机制检验只是启发性的。

4.1 匹配

已有文献指出，企业和工人之间更好的匹配通常出现在大城市，这是由于市场规模和工作技能要求之间的潜在互补性（Duranton and Puga, 2004）。更好匹配的优势可能仅存在于某些工作。我们关注学历过高（overqualification）是因为工作的程序性程度对于工人根据不同的受教育程度在不同的职业间分配具有重要意义(Autor, 2019)。因此，我们探讨就业密度和RTI对技能不匹配的影响。

技能不匹配有两个维度，第一个是“纵向”不匹配，指工人获得的学历高于目前从事工作要求的学历，也就是教育经济学文献中说的“学历过高”(Duncan and Hoffman, 1981)。在我们的样本中约有24%的人学历过高，图8展示了学历匹配程度与4分位ISCO职业定义的就业密度之间的关系。我们观察到学历过高工人占比高的职业通常集中在就业密度低的地区。第二个是“横向”不匹配（Boualam, 2014），测度了工作领域所需教育与工人实际获得的该领域教育之间的不匹配性。比如，当一个工人所受的训练是工程师，但最后成为一位银行经理，虽然两份工作所需的受教育水平相同，但是却被认为存在不匹配。

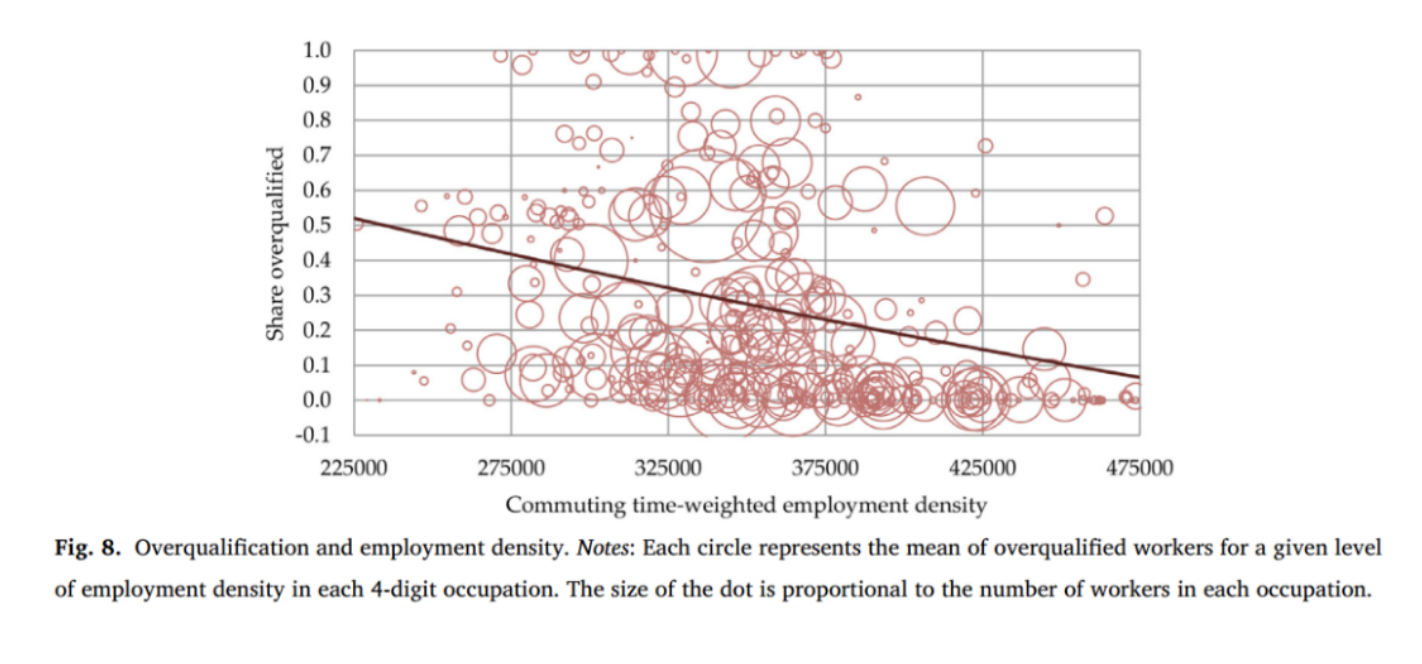
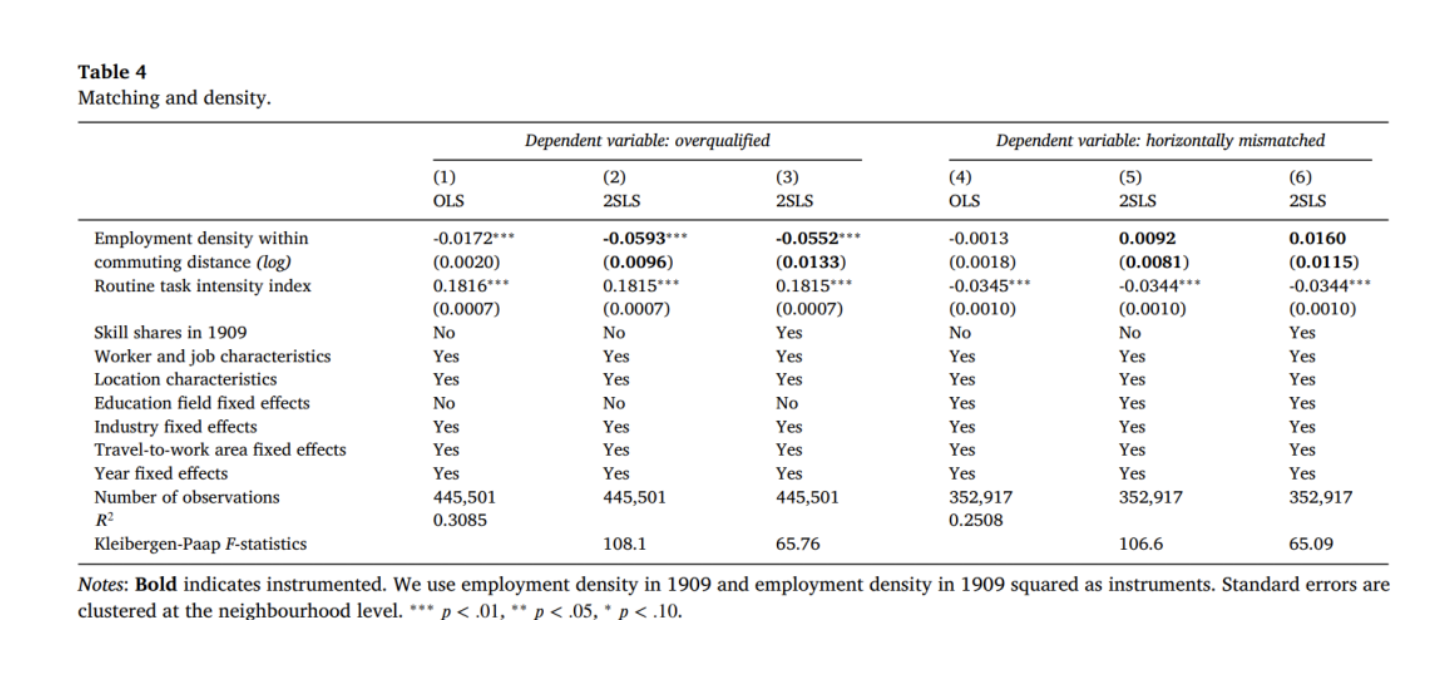
表4展示了就业密度对不匹配影响的回归结果。在纵向不匹配的回归中，我们删掉了受过初级教育的工人，因为他们处在职业阶梯的低端，因此不可能学历过高。在横向不匹配的回归中，控制了所在领域受教育水平的固定效应。表4第（1）列的回归结果显示，大城市工人获得的工作更可能与他们的受教育程度相匹配。就业密度每增加10%，纵向不匹配程度下降0.17个百分点。第（2）列使用了工具变量，第（3）列进一步控制了1909年不同技能水平的工人占比。第（4）-（6）列关注横向不匹配。因为缺失2013年以后所在领域受教育水平数据缺失，观测样本更少。我们并没有发现就业密度会影响横向不匹配，这与已有文献不一致（Boualam, 2014）。可能的原因是我们能更好地控制工人和区位特征，关注的是劳动力市场内部的横向不匹配。一个可能的解释是更多分析性任务密集的工作需要更少的专业领域知识。

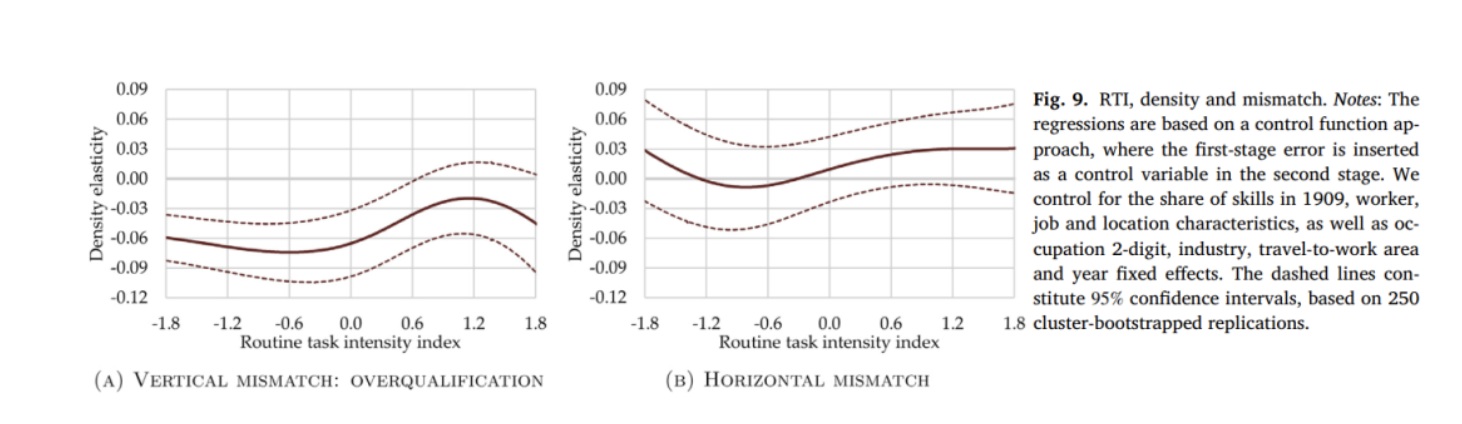
如果匹配是潜在的影响机制，那么不匹配程度低仅应该出现在低RTI的职业中。图9 Panel A 显示，对于较低RTI的职业，就业密度会显著降低纵向不匹配程度，说明纵向不匹配可能是图6的一个解释机制。Panel B显示，即使对于较低RTI的职业，就业密度也不会显著降低横向不匹配程度，说明横向不匹配不能解释对于从事分析性任务密集型职业的工人的工资-就业密度溢价。

4.2  学习

借鉴Davis and Dingel(2019)的结论，我们预期承担分析性任务的工人可以获得更多的学习机会。但是，DelaRoca and Puga(2017)的研究表明，学习机会不会立刻得到，而是随着在大城市待的时间增加而增加。为了捕捉学习效应，我们使用了两个比较粗糙的指标，第一个是劳动力市场经验，用年龄减去毕业年龄。由于随着年龄的增长经验增加，我们在回归中也直接使用年龄进行回归。第二个学习的指标是区位经验（locational experience），用一个工人在一个特定城市受雇用的年数来测度。如果一个工人在一个城市工作的时间越久，她/他更可能建立商业网络来获得集聚经济的好处。我们假设学习机会是动态的，随着经验的增加而增加。

表5第（1）列用于检验劳动力市场经验可以获得更高的工资-密度溢价。我们发现，对于没有经验的工人来说，集聚经济的影响很小。举例来说，对于一个刚进入劳动力市场的人来说，工资对于就业密度的弹性几乎为0，但是24年（经验的中位数）后，这一弹性增加到0.116。因此，更有经验的工人从集聚经济中获得更多的好处。一个可能的疑问是集聚效应来自于年龄。在第（2）列中，我们加入了就业密度与年龄的自然对数的交互项。我们发现，这一交互项不显著，但是就业密度与经验的交互项依然显著，甚至系数更大。第（3）列的结果表明，集聚经济随着区位经验的增加而增加，如果一个工人在一个地区工作10年，工资对就业密度的弹性会高出32%。由于数据限制，区位经验数据存在测量误差，第（4）列剔除了截尾观测值，回归结果是类似的。第（5）列同时加入了劳动力市场经验和区位经验与就业密度的交互项，结果显示集聚经济随着劳动力市场经验和区位经验的增加而增加，只不过区位经验的影响部分被劳动力市场经验吸收掉了。

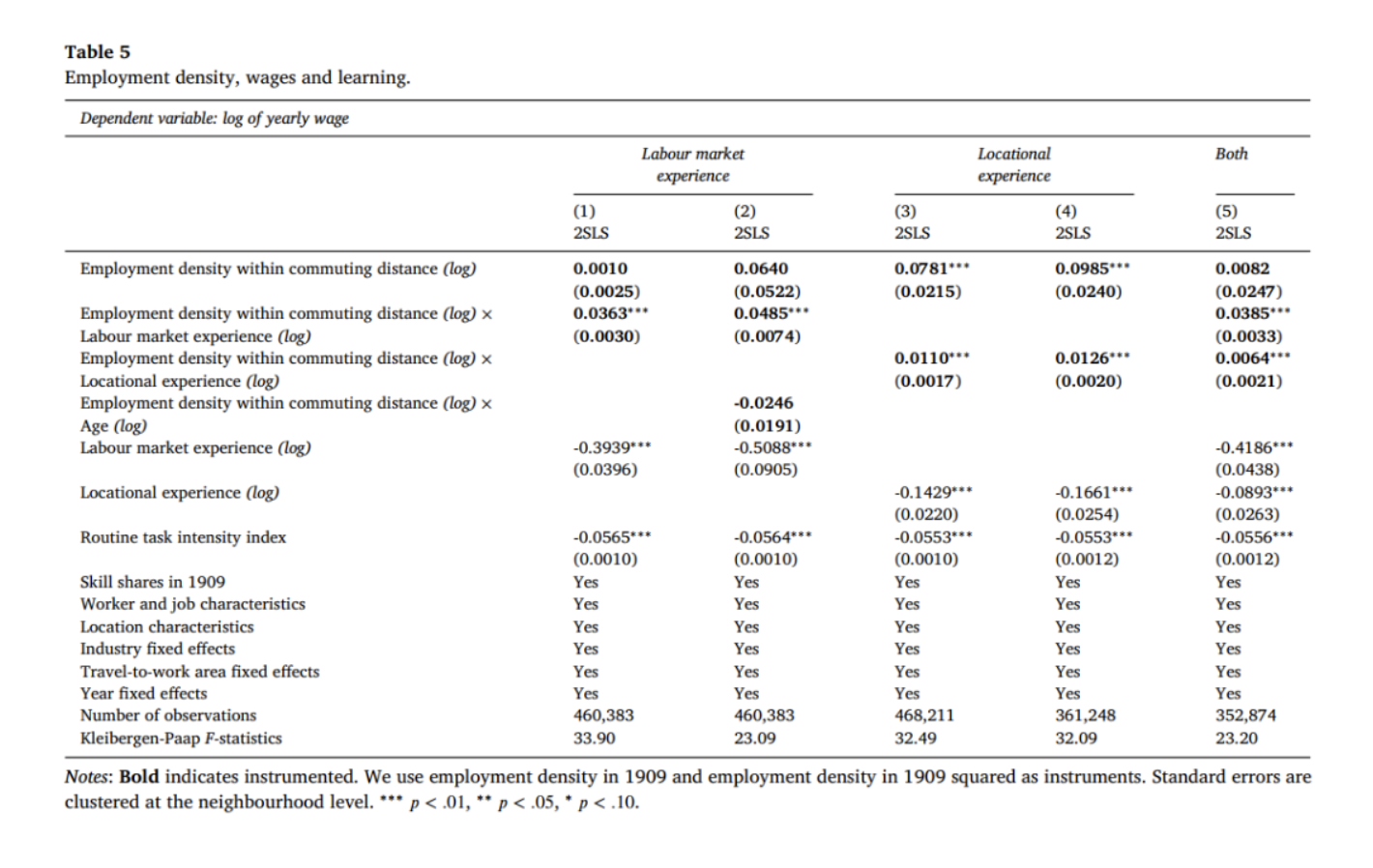
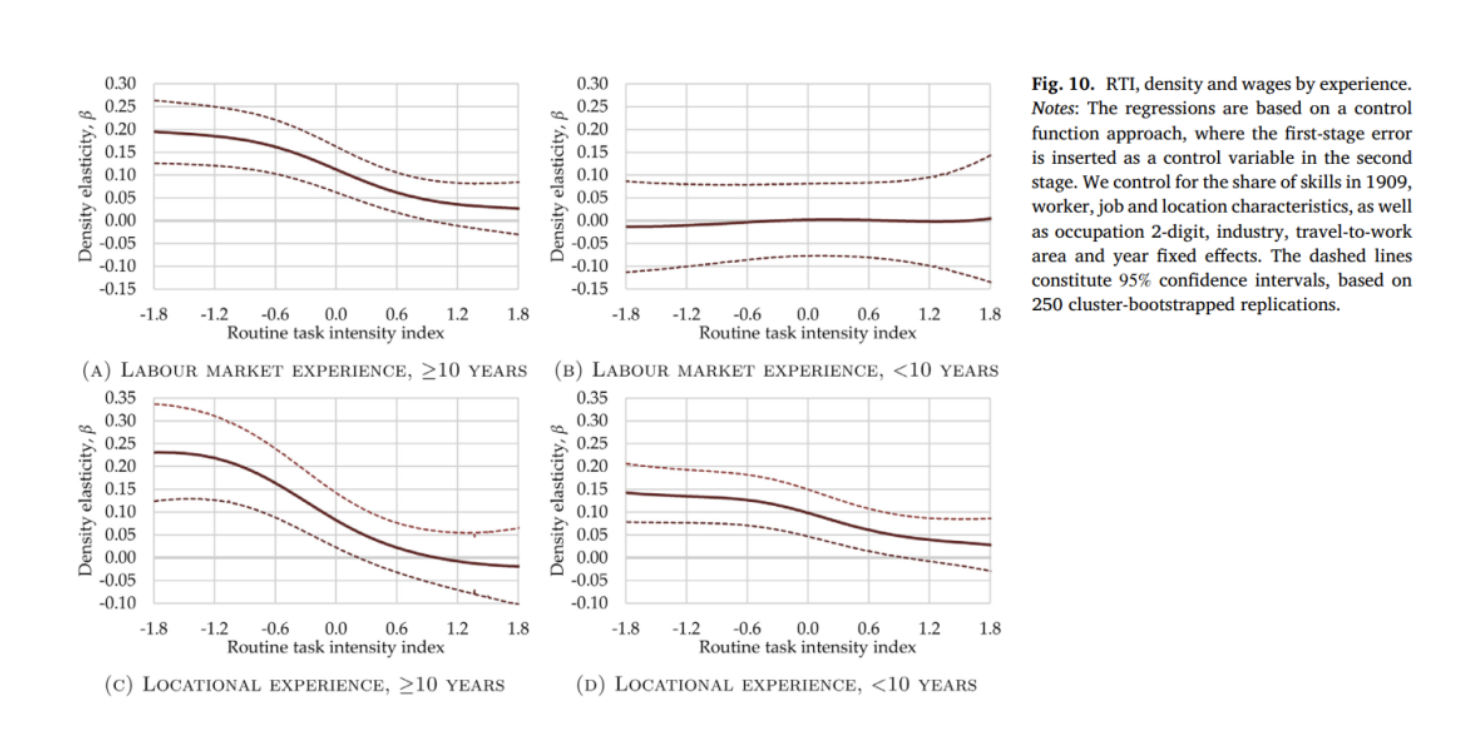
图10 根据工人的经验来分样本检验学习效应是否能够解释集聚效应随着RTI增加而减少。Panel A显示，对于那些劳动力市场经验超过10年的工人来说，RTI与工资-就业密度溢价的关系几乎与图6一致。Panel B显示，对于缺少劳动力市场经验的工人来说，无论从事哪种任务类型，几乎不能从集聚经济中获益，这表明学习效应随着工作经验的积累增加。总的来说，不管工人是否有劳动力市场经验，从事程序性任务密集型工作不能从学习效应中获益。我们也根据区位经验分类绘制图6，发现对于缺少区位经验的工人来说，RTI对工资-就业密度弹性的曲线更加平坦，也可以说明从事非程序性任务密集型工作的工人更多从学习效应中获益。

5、结论

关于城乡工资不平等已有诸多文献探讨（Wheeler, 2001; Baum-Snow and Pavan, 2013; Michaels et al., 2016），既有的劳动力市场模型仅仅区分工人的技能类型并不能完全解释城乡工资不平等。尽管许多研究探讨工资和就业密度之间的关系，但是就业密度提高生产率的异质性影响依然研究较少。此外，就业密度如何对工作任务的空间集聚以及工资产生影响更是未知的。

本文是第一篇使用雇员层面的数据来构建连续性的RTI指标，旨在探讨城市地区不断扩大的工资不平等的根源。本文创造地构造了使用通勤时间加权的就业密度指标和RTI指标，研究发现就业密度显著增加了非程序性任务密集型工作数量，就业密度对工资影响的系数与已有文献一致。另外，就业密度的工资溢价仅存在于从事非程序性任务密集型的职业。本文提供了匹配和学习机会两条潜在的影响机制。

城市是复杂工作的孵化器，从事复杂、分析性任务密集职业的工人可以获得更高工资，对于技术进步带来的自动化效应更加不敏感，并且有更大可能性找到与他们的受教育程度更加匹配的工作，因此，他们可以获得任务溢价。给定从事程序性任务的工人不具备上述条件，意味着城市地区承担不同任务的工人工资差距会拉大。因此，政策制定者应该投入更多资源在非程序性任务工人身上，提升他们的技能，更好地适应技术进步，减少工资不平等。