阅读:0
听报道
推文人 | 许文立,安徽大学经济学院、宏观经济研学会(CIMERS)
三、DSGE模型参数的校准与估计
目前,DSGE模型的参数估计并不意味着模型中所有参数都是用Moment Matching、Maximum Likelihood、Bayesian Likelihood等方法估计出来,往往是校准和上述三种方法结合使用。
上述四种估计方法中,前两种是有限信息法,后两种是完全信息法。下面,详细说说这四种方法:
3.1 校准
参数校准貌似是最为人们“嫌弃”,但又不得不用的方法。但是,我想说的是,这种方法在计量经济学会创会时,那些计量经济学的祖师爷们就开始在用了,而且它是所有后续三种方法的基石。
Kydland and Prescott(1982)用了一种方法将他们所分析的DSGE模型转换成了一种经验分析。他们所使用的方法就是校准联系。DeJong and Dave(2007)将这种方法称为MM\ML\BL的基础。
我们知道,在Lucas(1976)、Sims(1980)的批判下,概率论方法的估计与假设检验对结构模型不适用。因此,校准练习的目标是为了用参数化的结构模型来探讨一些特定的定量问题。Kydland and Prescott(1991,SJE;1996,JEP)追溯了校准练习作为一种经验研究方法的历史起源,大家可以去看看。在Economitrica的创刊语中,Frisch(1933a)指出:
“……[计量经济学会]要促进那些旨在统一理论定量方法与经验定量方法的经济研究,并鼓励那些具有建设性和严谨的思考……一切旨在进一步促进经济学理论与经验相统一的活动都属于计量经济学会感兴趣的范围。”
而且,Frisch(1933b)还利用微观数据来校准了生产技术参数,并用来研究经济周期冲击的传播机制。我们都承认这种方法存在一些缺陷,尤其是关于模型误设方面。但是,正如Prescott(1986)指出:
“所有构建在理论框架之上的模型必然是一种高度抽象的东西。因此,它们肯定存在模型误设问题,统计假设检验会拒绝它们。但是,这并不意味者我们不能从这些理论定量分析中学到一些有用的信息。”
总之,校准练习肯定是一种经验工具(DeJong and Dave,2007)。Kydland and Prescott(1996,JEP)指出:“一定要注意,校准并不是为了得到某些参数的大小,即它不是估计。”因此,在校准DSGE参数的时候,通常来源于两个方面:一是长期均值;二是微观证据的经验结果(例如,Cooley and Prescott(1995)就利用了Ghez and Becker(1975)的微观证据来校准参数)。
3.2 矩匹配
与校准比较,矩匹配法采用了经典统计理论。在这一理论下,模型被当作是一种源于实际数据的潜在的数据产生过程(DGP),也就是说,用于刻画数据的矩都是既定的。
在参数估计阶段,矩匹配过程就是要决定参数以使得结构模型最佳匹配预先选择的矩集合。实现这一目标的参数可以被认为就是这些参数实际值的估计量。
在检验阶段,检验的目标就是要决定所选择的矩集合是否能作为来自于结构模型的随机序列特征。如果与这一结果相关的概率小于某一临界值,那么,该模型就被拒绝作为一种潜在数据产生过程。
由于完成估计与检验的过程是基于预先选择的矩集合,而不是与模型相关的所有统计信息,因此,矩匹配法也被称为有限信息法。
其缺点为:完全信息法可以由对应的似然函数执行,但是矩匹配法则会导致一些效率损失,尤其在小样本情形下会有问题。因此,基于此的推断可能会对所选择的矩集合极其敏感。
其优点为:似然函数的建立要求假设结构冲击的分布。但矩匹配法并不要求这个假设,除非要进行模拟练习,因此,该方法并不受潜在模型误设问题的约束。
此外,矩匹配过程至少可以追溯至Pearson(1894)年。且这里的矩匹配包括三种方法:广义矩匹配法(GMM)、模拟矩匹配法(SMM)和间接推断(II)。
3.3 极大似然和贝叶斯方法
与第二类估计方法相比,极大似然估计和贝叶斯方法都属于完全信息法。在这些方法下,DSGE模型被视作以似然函数的形式为数据提供了完全统计特征。似然函数是由观测数据的状态空间表示与模型中的随机扰动的分布假设相结合而成。
与有限信息法相比,完全信息法有两个特征:1)假设随机扰动的分布:推断是基于模型结构和分布假设的联合条件分布;2)推断是基于模型的完全信息。
经典法与贝叶斯法相比:1)在经典法下,参数是固定的(但未知),而数据是来源于对应似然函数的随机序列。那么,参数估计就要最大化似然函数,且与原假设对应的似然函数被用来评价观测数据有多大可能由原模型中产生。2)在贝叶斯方法下,参数是随机的,而数据则是已经实现的。那么,估计过程的目标就是要使得模型参数用条件概率表示。以概率表示的参数可以正式合并一些有关先验设定的信息。即通过贝叶斯法则将先验分布与似然函数相结合,得到参数的后验分布。而后验分布的均值或模则为参数提供了点估计值,而与估计相关的不确定性则由后验标准差给出。而推断则是比较一个模型的条件概率与另一个模型的条件概率。
贝叶斯方法的目标是:1)利用缩减形式模型(例如VARs)的参数作为先验信息的一种来源而被用于DSGE的定量分析;2)促进了DSGE模型参数的直接估计;3)促进了模型之间的比较。
总之,评价一个模型1)在极大似然法下,就要回答下列问题:给定原假设,观测数据有多可信?2)在贝叶斯方法下,要回答的问题是:给定观测数据,一个模型的可靠性比另一个模型高多少?
3.4 应该选择哪种方法呢?
目前,比较估计方法的文献资料较少,据我所知只有Ruge-Murcia(2007)、Canova(2007)、Hashimzade and Thornton(2013)(只是稍微提及了一下)、DeJong and Dave(2007)。
参数估计主要关注两个问题:模型误设和奇异性。
首先,联合估计结构模型系统具有一些优势(经济意义和统计意义),同时也有一些劣势:1)优势在于,从经济角度看,参数估计使用了模型的所有信息这一点十分具有吸引力;从统计角度看,当所有可利用信息都被使用时,统计效率会提升。2)劣势在于,tight parameter estimates往往从经济角度看不太合理,而且很难证明其恰当性,这就会导致理解困难。
其次,模型误设至少从以下两条渠道对完全信息估计技术带来挑战:1)当冲击数量小于内生变量数量的时候,参数就从受限的时间序列中估计,这就将完全信息方法转换成了有限信息方法。而且不能保证所有变量都有相应的信息,因此,就需要我们进行试验,而这种试验又缺乏经济和统计理论指导。2)如果模型就是一个数据产生过程(DGP),那么,完全信息估计和检验都会存在问题。
这些问题也有一些解决方案(不完美):
1) 增加测量误差可以消除系统的奇异性,但是不能修正动态误设问题;
2) 增加序列相关的测量误差可以解决上述两个问题,但是这种方法缺乏经济基础;
3) 贝叶斯方法可以处理这些问题。先验信息起到了惩罚函数的作用。如果先验信息比较恰当,那么,这种方法可以使得完全信息法找出一个局部,但是经济上有价值的最大化值。此外,它还可以降低ML估计的偏度和峰度。而且,MCMC方法已经被证明具有良好的规模和性质。但是,仍然还有许多工作要做(Canova,2007)。
3.5 先验分布的选择
在贝叶斯估计过程中,关于估计参数的先验分布选择,有许多经验法则。一般来说,我们可以将参数划分为三种类型(参见Del Negro and Schorfheide(2008)、Herbst and Schorfheide(2015)):1)第一组包含影响DSGE模型稳态的参数;2)第二组包含那些刻画了外生冲击过程的运动法则;3)第三组包含那些不影响模型稳态,但却控制了内生传导机制的参数。
在将参数集划分成上述三种类型后,我们就可以考虑这些参数的合理先验区间。实践中,
1) 我们通常利用样本期之前的平均值来得到影响稳态的参数先验分布;
2) 第三组参数则要利用微观计量证据来声明先验分布;
3) 第二组参数通常不可观测,因此其先验分布也最难以设定。但Herbst and Schorfheide(2015)给出了一种迭代过程来获得它们的先验分布:1.设定先验分布;2.从该先验分布中提取抽样;3.根据DSGE模型模拟生产变量数据,利用模拟轨迹计算样本矩;4.评价样本矩的先验分布的合理性;5.调整先验分布,直到样本矩先验分布与先验信念一致。
通常根据参数定义域来选择分布。例如,如果参数定义域为实数域,先验分布可以选择正态分布;如果参数定义域为非负,先验分布可以选择对数正态分布、伽马分布或者逆伽马分布;如果参数定义域有有界区间,先验分布可以为截断正态分布或贝塔分布。E. Sims(2017)给出的经验法则是,如果参数在[0,1],用贝塔分布;对于冲击的标准差,用拟伽马分布;而另外一些参数,要么用正态分布,要么用伽马分布。
最为重要的是,这些先验分布可能有些随意,并带有主观性,因此,一定要做敏感性检验。这也是大部分高质量DSGE文献所必备的内容。
四、DSGE模型的使用
虽然全球金融危机给DSGE带来了许多批评和指责,但不可否认,它仍然是目前宏观经济与政策分析的主流模型。
3.1 课本中的DSGE模型
本文以两本流行的中级宏观经济学教材——Blanchard(2017)的《Macroeconomics(7th edition)》和Mankiw(2015)的《Macroeconomics(9th edition)》——为例来说明,危机后的宏观经济学教学中DSGE的使用。
Blanchard(2017)在其最新修订出版的《Macroecconomics》(第七版)中,根据全球金融危机的启示,修正了传统宏观经济学的分析框架,尤其是将传统的产品市场和货币市场均衡扩展至产品市场、金融市场和劳动市场均衡。并用IS-LM-PC模型代替了传统的总供给-总需求模型,其中货币政策从数量型转换成价格型的泰勒规则,而且整个分析框架引入了预期。并利用该框架分析了产出和通胀的动态特征,财政政策冲击以及供给冲击的动态效应。
Mankiw(2015)在其《Macroeconomics》(第九版)中,将解释短期波动的模型称为动态总供给-总需求模型(动态AD-AS模型)。他反复强调,该模型注重分析宏观经济的动态特征。且经济会持续不断地遭受许多冲击,这些冲击不仅会立即对短期宏观经济产生影响,还会影响到产出、通胀和其它宏观经济变量的动态演变路径。它也强调,该动态AD-AS模型刻画了现实的货币政策,即央行根据通胀和产出来设定目标通胀。
至此,虽然Blanchard(2017)和Mankiw(2015)均没有使用更正式的DSGE模型,但不难看出,他们所使用的动态宏观经济模型均为三方程NK模型。
“如果你们还要继续学习宏观经济学的高级课程,那么,你们极有可能学习到DSGE模型。……本书呈现的动态AD-AS模型就是DSGE模型的一个简化版本。虽然,该模型没有高级版本DSGE模型那样专业。但其宏观内核与更专业的DSGE模型一样。动态AD-AS模型是初级水平的AD-AS模型与高级DSGE模型之间的阶梯。”(Mankiw,2015:p.471)
3.2 学术研究中的DSGE模型
全球金融危机被认为是大衰退以来最大的经济危机。虽然两者相隔近一个世纪,但这场危机又让我们回到了与大衰退相同的经济环境(Krugman,2011)。Kehoe et al.(2018)在比较了美国1982年经济衰退与2008年全球金融危机之后,更是得出:“随着时间的推进,宏观经济学家所要分析和解决的基本问题并没有变化。”
Kehoe et al.(2018)进一步指出,经济周期方法的发展则从根本上改变了这些问题提出和解答的方式。不再提问“我们今天能采取的最优政策是什么?”,而是问“在不同政策措施下,经济会如何演化?”。而回答这些问题则是依据更加具有微观基础的动态结构模型。
当然,宏观经济学家仍然对这些根本性的问题持有多样化的观点。但他们也基本同意,对于这些问题的分析、讨论与交流必须要用动态一般均衡模型的语言来进行。
3.3 政府机构的DSGE模型
纽约联储的经济学家Del Negro and Giannoni(2017)认为,从理论上来说,DSGE模型是一种理想的政策分析工具。而这种估计的模型可以回答政策制定者脑海里的许多政策问题。Christiano et al.(2018)简短地描述了美国联邦公开市场委员会(FOMC)的决策过程。FOMC在开会决定政策之前,会议的每位参与者都会收到被称为Tealbook的文件。这些文件里包括联储员工根据模型模拟出的许多政策方案产生的经济效果。这些模型包括DSGE模型、SIGMA和EDO。
而纽约联储的DSGE模型早在2004年就以三方程NK模型形式存在(Sbordone et al., 2010)。直到2008年,Del Negro and Schorfheide(2008)构建的中等规模DSGE模型——结构类似于Christiano et al.(2005)和Smets and Wouters(2007)——来取代三方程NK模型。2010年中期,中等规模的DSGE模型才开始用于预测,且只在FOMC内部作为参考。受到金融危机的影响,该模型引入了金融因素。并于2011年6月开始,具有金融摩擦的纽约联储DSGE模型的预测结果正式进入了FOMC一年发布四次的备忘录中。2014年末,Del Negro and Schorfheide (2013) 和Del Negro et al. (2015a)又开发了一个新的带有金融摩擦的NK模型。2015年-2016年早期,纽约联储的DSGE模型又进行了两次修正、升级,主要是修正和增加了用于估计模型结构参数的宏观时间序列。从2014年9月开始,纽约联储的DSGE模型的预测结果会向公众每年公布两次,2017年上半年开始,公布频率又提高到每年四次。[1]
除了美联储在使用DSGE模型进行宏观经济模拟与预测之外,世界其他国家的政府机构和国际组织也都建立了各自的DSGE模型来分析宏观经济,例如欧洲央行的NAWM、加拿大银行的Totem、英格兰银行的BEQM、日本银行的JEM、欧洲委员会的QUESTIII以及国际货币基金组织的GEM等。此外,以色列央行、捷克国家银行、瑞典央行、瑞士国家银行等也在使用DSGE模型的分析结果作为政策决策的参考。[2]
下面,我们来看看我们与中国人民银行合作的一个用DSGE模型进行预测的项目结果。图1和2都呈现了DSGE模型对我国2018年1月-2019年6月的CPI环比值的预测结果。图13-1除了预测期外,还包含了1990年1月-2017年12月的模型模拟值、1990年1月-2018年7月的实际CPI环比值。而图13-2则只显示了2018年1月-2018年7月的实际CPI环比值以及2018年1月-2019年6月的预测值。
从图1可以看出,本课题构建的DSGE模型对我国1990年1月-2017年12月的336个CPI观察样本的拟合程度非常好。因此,可以利用该DSGE模型对2018年1月开始的18个月的CPI环比值进行预测。图中蓝色线条表示DSGE模型给出的2018年1月-2019年6月的18个CPI点预测值,而绿色虚线则表示90%的预测置信区间。
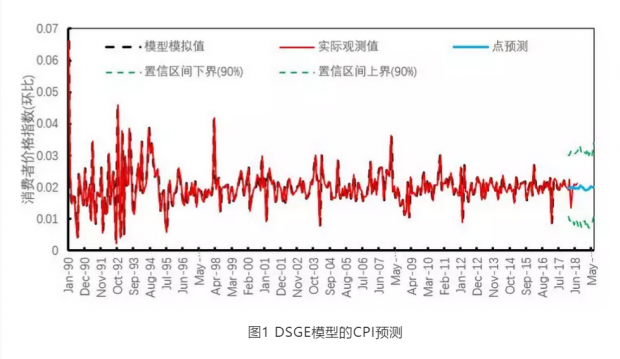
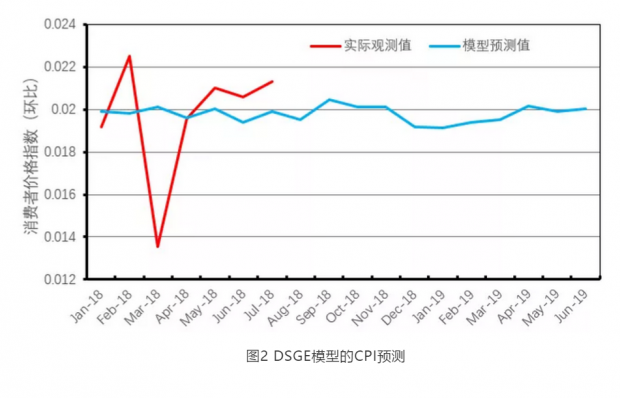
图2只呈现了2018年1月-2019年6月期间的CPI样本数据与预测值。从图中可以看出,2018年1月-3月的CPI预测值与实际CPI变化趋势不一致,但是从2018年4月开始,接下来四个月的CPI预测趋势与实际CPI的变化趋势基本一致。基于DSGE模型的预测,2018年下半年,我国CPI的环比走势会上升,而从2018年年底-2019年上半年,我国CPI环比走势则会下降。
五、结语
现在,学界基本已经形成一致意见:NK-DSGE模型显然不适应危机后的经济情形。正如Blanchard and Summers(2017)指出,如大衰退和滞胀一样,这次金融危机必然会对宏观经济学带来深远的影响。这次危机会使得宏观经济学作出哪些改变仍然还在争论中。不过,似乎大部分学者都同意,宏观经济学会不断演进,而不太会出现“革命”(Vines and Wills,2018)。而对于宏观经济模型来说,需要重构基准模型结构也已经成为共识。
基准模型中应该包括哪些核心结构, Blanchard(2018)认为金融摩擦、价格粘性、有限时期和自有资金应该包含其中;而Vines and Wills(2018)、Stigliz(2018)、Wright(2018)、Ghironi(2018)等虽有不同的看法,但他们都同意在基准模型中引入金融因素。而且学界已经有很多这方面的研究成果,如前文所述。
之所以没有提到引入“房地产部门”,一方面,是因为宏观经济模型中的房地产建模也已经有很多了。但更为重要的是,我并不认为“房地产部门”应该作为未来基准模型的核心结构。它更像是一种“临时设置的结构”,为了解释这次危机的起源和传导机制。这就像有学者说,宏观经济学或者宏观经济模型只是再让人们不再犯同样的错误。因此,Blanchard(2017)说:“如果危机还能给我们什么启示的话,那可能是危机总会以我们意想不到的方式出现。”
那么,大家为什么会觉得基准模型里要包含金融因素呢?难道仅仅是因为这次全球金融危机,那会不会也是“临设结构”?关于在基准模型中引入金融因素的论述非常多,在这里,引用Reinhart and Rogoff(2009)的“This time is different: eight centuries of financial folly”前言里的一段话:
“如果非要从本书分析的这么多危机中提炼出一个共同的主题,那肯定是过度的债务积累,无论是政府、银行、企业还是消费者。过度的债务积累经常会导致非常严重的系统性风险。过多的现金供给会使得政府看起来在为经济强劲增长提供了更大动力,但实际上却不是。私人部门借过度的债会使得房产和股票价格虚高,从而远超其长期可持续水平,进而使得银行部门看上起更加稳定,且盈利更多,但这都是假象。如此大规模的债务积累会带来风险,因为它们会使得经济体系对信心危机极为脆弱,尤其是当债务是短期的,并需要持续不断的融资。靠债务支撑的繁荣经常会导致政府决策失误、金融机构的经营决策失误以及人民生活水平的盲目。因此,历史上,大部分的经济扩张都是以极坏的结果收场。”
因此,不应该将长期关注点聚焦于某个或某些“临设结构”,而应该思考未来宏观经济模型的基准结构应该包含哪些。
一些经济学家认为形式上更加简洁的IS-LM模型同样可以对危机作出解释,并成功预测经济的发展(例如,Krugman,2016)。在他们看来,利用DSGE模型的研究,则没有对未来作出任何有意义的指导。
不可否认,有些DSGE模型假设确实与经验事实(或者微观证据)相偏离。但这也正是DSGE不断改进之处。该模型也在许多经济领域成功应用(Prescott,2016)。至于其数学结构的复杂性,正如Farmer(2014)指出:
“从19世纪后期以来,数学形式对于我们来说已是不可或缺的工具。如1947年萨缪尔森的《经济分析基础》和1989年斯托克-卢卡斯的《动态经济学的递归方法》所带来的跃进。……正如1906年马歇尔写给鲍利的信中所言,数学只是一种语言,其它什么都不是。……而DSGE所拥有的巨大数学优势,为我们提供了逻辑工具,从而使得我们能整合许多感兴趣的研究内容。”
我们在评价一个东西的好坏时,总需要事先确定一个评价标准(Korinek,2015)。而对于宏观经济学来说,有的人追求宏观经济理论的“纯粹性”,有的人则更在意其对现实的解释与预测能力。这就是我们所熟知的作为“科学家”的宏观经济学家和作为“工程师”的宏观经济学家(可参见Mankiw,2006)。
不同的视角,不同的目的必然也会导致评价结果存在差异。政策制定者更加关心现实经济的运行与发展趋势。只要有助于经济政策的制定,任何模型都可以用来进行政策分析,这其中当然包括DSGE模型。而宏观经济学家所进行的学术研究,则更注重于经济机制与思想性,注重经济模型的严谨性与科学性。但是,过去20多年中,政策制定者与宏观经济学家之间更多地是相互依赖,相互促进的关系(Woodford,2009;Kocherlakota,2016)。
到目前为止,宏观经济学的分歧远远没有(外人)看上去那么大。从理论上,争论小得多。Friedman(1968)指出,宏观经济最大的分歧在于政策应该取得什么效果,以及政策能不能取得这些效果。而政策又是大众最为关注的,因此,争论才会被放大,共识则被忽略了。
“虽然宏观经济学中仍有大量问题和观点存在分歧,但是,相比于过去,宏观经济学家对于宏观经济学中一些根本性问题已经形成了相当多的共识。……当然,宏观经济学中确实还有大量问题和分歧有待解决,但是就目前来讲,理论和经验研究之间、理论与实践之间富有建设性的探讨越来越多,且会持续推动宏观经济学的发展。”(Woodford,2009)
[1] 纽约联储DSGE模型的结构、参数先验分布、数据以及估计过程的详细资料,可以参见Del Negro and Schorfheide (2008)、Del Negro et al. (2013,2015,2016)。
[2] 各国央行与国际组织使用的DSGE模型详细描述可以参见,Smets et al.(2010)的欧洲央行DSGE模型、Carabenciov et al.(2013)和Freedman et al.(2009)的IMF全球DSGE模型、Benes et al.(2014)的IMF宏观审慎模型、Vitek(2018)的IMF全球宏观金融模型GFM、Clinton et al.(2017)的捷克央行DSGE模型、Adolfson et al.(2013)的瑞典央行的DSGE模型、Argov et al.(2012)的以色列央行DSGE模型、Dorich et al.(2013)的加拿大央行DSGE模型、Alpanda et al.(2014)的加拿大宏观审慎模型、Rudolf and Zurlinden(2014)和Gerdrup et al.(2017)的瑞士央行DSGE模型。

话题:
0
推荐
财新博客版权声明:财新博客所发布文章及图片之版权属博主本人及/或相关权利人所有,未经博主及/或相关权利人单独授权,任何网站、平面媒体不得予以转载。财新网对相关媒体的网站信息内容转载授权并不包括财新博客的文章及图片。博客文章均为作者个人观点,不代表财新网的立场和观点。




 京公网安备 11010502034662号
京公网安备 11010502034662号 