图片来源：百度图片

原文信息：

Broderick T, Giordano R, Meager R. An Automatic Finite-Sample Robustness Metric: Can Dropping a Little Data Change Conclusions?. arXiv Working Paper, July 2023.

写在前面

01

假设一项研究的结果在删除很小一部分样本后就会发生巨大的改变（例如从正向显著变成负向显著），那么该原始结果和数据处理过程的可靠性便大打折扣。换言之，由于对数据的来源、质量、分布等方面没有足够的了解和控制，就可能会因为数据的不完整、不准确或者不具有代表性而得出错误或者不可靠的结论，即所谓的数据稳健性（Data Robustness）问题。例如，如果删除不到1%的数据就可以改变效应的符号、显著性或者置信区间，那么就有理由怀疑此效应是否真实存在，抑或是否受到某些混杂因素或遗漏变量的影响。有鉴于此，MIT的Broderick等学者早新近工作论文《An Automatic Finite-Sample Robustness Metric: Can Dropping a Little Data Change Conclusions?》中，提出了一种评估应用计量经济学结论对数据子集敏感性的方法，为稳健性检验提供了新途径。

囿于篇幅，下文仅就原作中核心方法和结论作简要介绍，具体数理推导和计量分析的细节可参见原文及其在线附录。

02

研究背景

理想状态下，政策制定者可将经济学研究作为有关民众生计、健康和幸福决策的参考。然而，研究所用的样本可能与决策的目标人群存在非随机的差异——这可能源于获得完全随机的样本并非易事，也可能源于不同时空状态下人群间存在的差异。当这些偏离理想随机抽样的样本比例较小时，人们可能认为实证结论仍适用于受政策影响的人群。故值得考虑的是，删除很小比例样本数据（或少量数据点）是否会改变既有研究结果。有鉴于此，本文中作者提出了一个有限样本、可自动计算的指标，用以验证少量数据能否及如何改变实证结论。本文通过复刻数个经济学知名研究中的实证结果证实，即使在标准误差很小的情况下，删除不到1%的样本也可完全逆转其部分实证结果。

实证结论是否在很大程度上受有限样本中少数样本影响的原因如下：其一，在实际中，即使可从直接目标人群中抽样，仍然会有一部分数据缺失——这些个体或无法被调查员和执行者找到，或拒绝回答问题，抑或回答在数据处理过程中丢失或混淆。由于上述数据缺失不能被轻易地假设为随机的，因此，研究人员可能关心其实质性结论是否可能被缺失的少数数据点所推翻。其二，受少量数据点影响较大的结论更容易在数据分析过程中受到不利事件或错误的影响，包括p-hacking（即P值操纵）等，即使这些错误并为有意为之。

尽管可从给定的研究人群中构建一个理想的随机样本，但政策目标人群往往与研究人群有所不同（如研究和决策之间可能存在时间上的差异）。因此，学者们通常试图揭示关于世界的一般性或“外部有效性”的真理，并提出具有普适性的政策建议。

近似最大影响扰动（AMIP）稳健性的提出

03

为检验删减一小部分样本对计量结果的影响，最直接的方法是遍历所有可能的数据子集并重复回归。但在实际中，要检验所有可能的数据子集对结论的影响非常耗时和且难以实现。那么，如何检验既有结果是否稳健？是否存在一种通用且有效的方法，可用于评估删除一小部分数据会不会改变既有结论？

为回答上述问题，在本文中，作者提议直接测量样本中一小部分数据对研究的核心主张或结论产生影响的程度。对于特定的数α（如α=0.001），可找到不超过全部观测点的100α％的集合，当将数据从样本中剔除时，会对估计值产生最大变化，并报告这种变化。例如，假设在实施某些经济政策干预之后发现家庭消费出现了统计上显著的增加。进一步假设，通过剔除0.1％的样本（通常少于10个数据点），反而发现了统计上显著的减少。那么，很难确保即使在略有不同的人群中，政策的干预也会导致消费增加。为量化此类敏感性，可考虑数据集每个可能的1-α部分，并在所有数据子集上重新运行之前的分析（但这种直接实现在计算上是不可行的）。

鉴于此，Broderick等作者提出了一种快速近似方法，并称之为“近似最大影响扰动”（Approximate Maximum Influence Perturbation，简称AMIP）。如AMIP较小，则有理由认为实证分析是AMIP稳健的（或称具有AMIP稳健性），反之亦然。AMIP基于经典的“影响函数”（Influence Function），该函数在既有文献中被广泛用于评估对删减一个或少量数据点的敏感性。相比之下，作者将“去除非消失比例数据点的影响”与经典推断相结合，重点关注于推广到未知人群，而非检测明显的异常值，并分析了经验影响函数作为固定比例遗漏数据的近似精度。

作者证实，AMIP具有以下几个优点：

（1）适用于很多常见的统计方法，包广义矩估计法（GMM）、普通最小二乘法（OLS）、工具变量（IV）、最大似然估计（MLE）、变分贝叶斯（VB）等；

（2）可在有限样本下给出准确和有效的近似，而且还可以给出一个精确的有限样本下界；

（3）受推断问题中信噪比（Signal-to-noise Ratio，即信号方差与噪音方差之比）的驱动，且不受标准误差、渐近性质或模型设定的影响。

针对AMIP稳健性的检验，作者在线提供了名为“zaminfluence”的相应R包与教程（见https://github.com/rgiordan/zaminfluence）。

04 

知名实证案例的复刻和AMIP的应用

本文对一些基于随机对照实现（RCT）的经济学实证案例进行复刻以展示AMIP的应用，并发现提出的AMIP法捕捉到的敏感性在实践中变化很大。在复刻过程中，相较于原有实证结果（Original Estimate），作者分别展示了在删除少量样本的情况下，被复刻论文主要估计结果参数符号逆转（Sign Change）、显著性改变（Significance Change）以及参数符号显著逆转（Significant Sign Change）的情况（即评估需要删除多少数据点才能改变符号、显著性，或者生成与全样本估计结果符号相反的显著结果）。尤其值得注意的是，即使是一些发表在American Economic Review等顶级期刊上的具有广泛影响力的论文，其部分结论依然可能会因删除不到1%的数据被推翻甚至颠覆。具体案例如下：

案例1：美国俄勒冈州医疗补助RCT（Finkelstein et al.，2012）

复刻结果表明，对于大多数结果，删除不到1%的样本可产生与全样本分析相反的显著结果。在个别情况下，删除不到0.05%的样本可改变结果的显著性（见表1和表2，其中表1为基于IV的回归结果，表2为基于OLS的回归结果）。

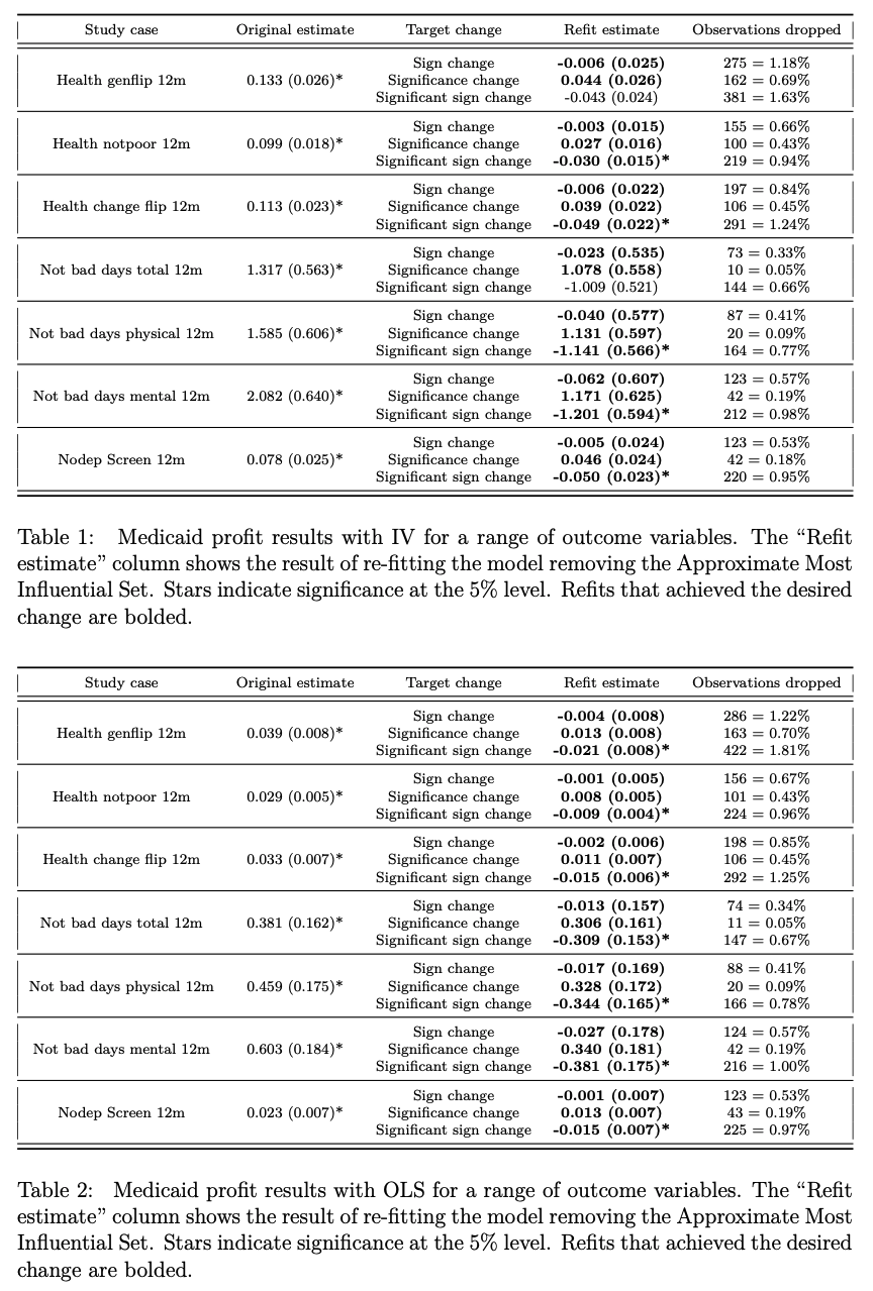
案例2：墨西哥“进步项目”（Progresa）现金转移RCT（Angelucci和De Giorgi，2009）

对于该研究的复刻表明，整体上在样本数据中剔除异常值并不一定会减少敏感性。具体而言，尽管对贫困家庭的分析相当稳健，但对非贫困家庭（Progresa实际影响群体）的分析要敏感得多（见表3）。

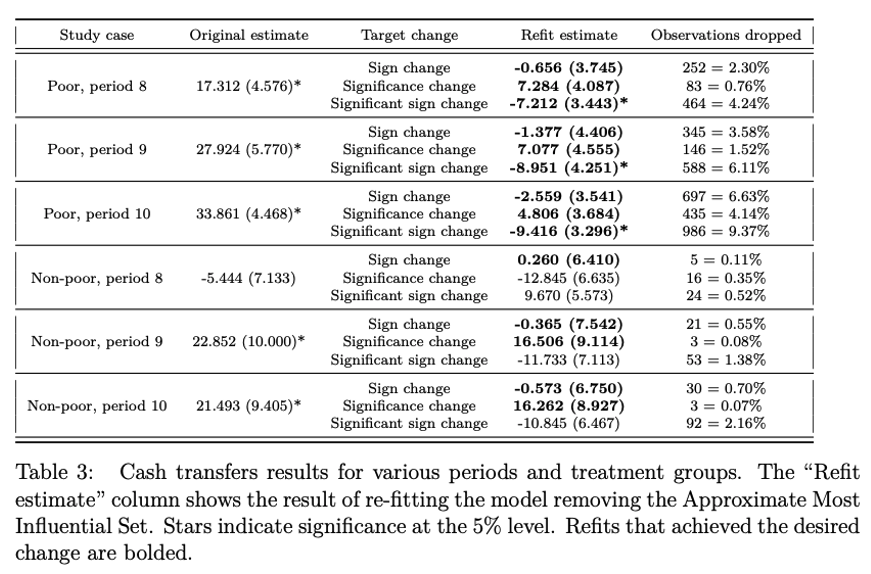
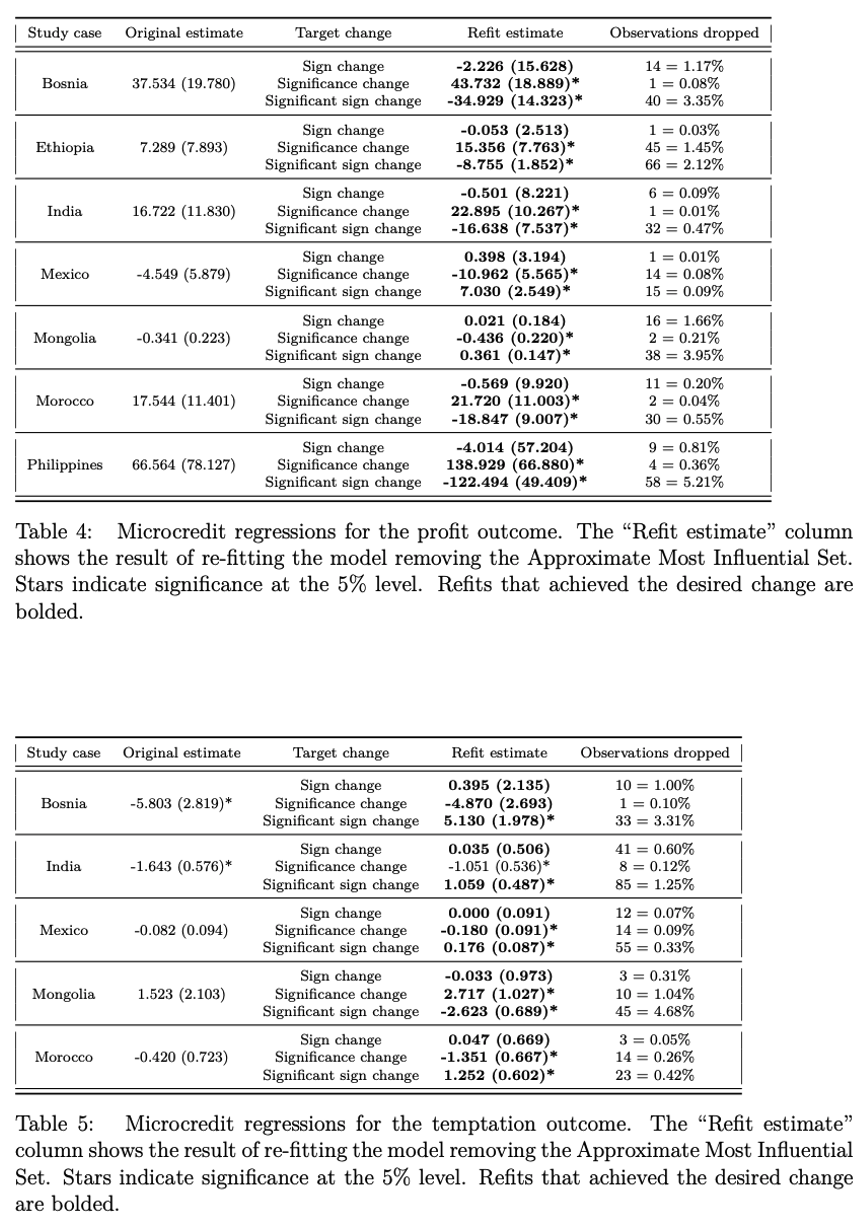
案例3：小额信贷RCT：7个简单两参数线性回归（Angelucci et al.，2015；Attanasio et al.，2015；Augsburg et al.，2015；Banerjee et al.，2015；Crépon et al.，2015；Karlan and Zinman，2011；Tarozzi et al.，2015）

对于此7项被公认为理解小额信贷影响最坚实之证据的研究，仅需通过删除不到1%的数据点，便可使其估计结果的符号或显著性发生变化（见表4和表5，其中表4为小额信贷对收益的影响，表5为小额信贷对诱导性消费的影响）。其中，墨西哥小额信贷RCT研究样本量最大，但也最敏感，其使用16561户家庭数据所得到负向估计系数，仅需去除15个数据点便可被彻底颠覆——撬动既有结论仅需不到1‰的样本数据！

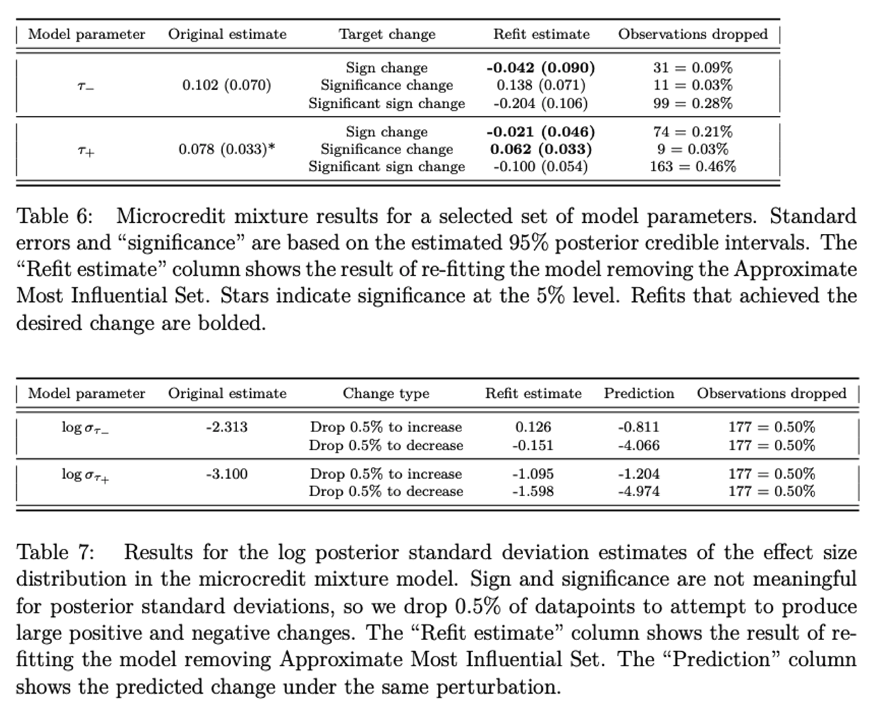
案例4：小额信贷RCT：贝叶斯分层分析（Meager，2020）

分析表明，简单和相对复杂的贝叶斯模型均无法免疫于剔除小部分数据所带来影响（见表6和表7，其中表6基于默认的既定模型参数，表7基于对数后验标准差估计）。

但同样需强调的是，并非所有结果的复刻都不稳健——基于AMIP检验，某些结果在剔除5%甚至10%的数据之前都是稳健的。这些案例表明，在经济学研究中，数据敏感性指标是一个非常有用且有意义的工具，可帮助研究者评估数据质量和稳健性，并且提高对推断结果的信心。

本文对经济学研究带来的启示

05

在经济学研究中，数据分析的稳健性是一个重要的问题，它关系到实证结论是否可信、是否能够推广到更广泛的人群和情境。故在进行数据分析时，应考虑到数据的来源、质量、分布等因素，及可能存在的数据偏差和不确定性。

本文证明，AMIP指标是一个有用的工具，其可评估删除少量数据对结果的影响程度，以及哪些数据点对结果有较大的影响力。借助AMIP，可以检验数据分析的稳健性，判断是否需要进行更深入的敏感性分析，以及是否需要收集更多或更优质的数据。此外，AMIP还可提高数据分析的透明度和可复制性，使其他研究人员能够更容易地理解和验证研究结果。在文章中，通过公开AMIP的计算方法和结果，可以向其他研究人员展示研究结果的稳健性，以及是否受到特定数据点的影响。如此，方可进一步提升研究质量和信誉，及促进学术交流和合作。

Abstract 

Study samples often differ from the target populations of inference and policy decisions in non-random ways. Researchers typically believe that such departures from random sampling — due to changes in the population over time and space, or difficulties in sampling truly randomly — are small, and their corresponding impact on the inference should be small as well. We might therefore be concerned if the conclusions of our studies are excessively sensitive to a very small proportion of our sample data. We propose a method to assess the sensitivity of applied econometric conclusions to the removal of a small fraction of the sample. Manually checking the influence of all possible small subsets is computationally infeasible, so we use an approximation to find the most influential subset. Our metric, the “Approxi- mate Maximum Influence Perturbation,” is based on the classical influence function, and is automatically computable for common methods including (but not limited to) OLS, IV, MLE, GMM, and variational Bayes. We provide finite-sample error bounds on approximation performance. At minimal extra cost, we provide an exact finite-sample lower bound on sensitivity. We find that sensitivity is driven by a signal-to-noise ratio in the inference problem, is not reflected in standard errors, does not disappear asymptotically, and is not due to misspecification. While some empirical applications are robust, results of several influential economics papers can be overturned by removing less than 1% of the sample.

声明：推文仅代表文章原作者观点，以及推文作者的评论观点，并不代表香樟经济学术圈公众号平台的观点。