推文人 | 杨冬

 

原文信息：Götz, T. B., Hecq, A., & Urbain, J. P. (2014). Forecasting Mixed-Frequency Time Series with ECM-MIDAS Models. Journal of Forecasting, 33(3), 198-213.

研究介绍

 

在经济学中，我们经常会遇到抽样频率不同的宏观经济数据。其中一个例子就是用工业产品指数等月度数据和利率或者股票价格等日度数据预测季度GDP。处理该问题的传统方法是对高频数据进行加总合并，即所有变量均以最低频率出现。然而这一方法会由于忽略高频数据样本而导致大量信息的损失。在许多情况下，考虑到低频被解释变量的观测数量，包含所有潜在的高频解释变量是无法实现的。为了保证所有高频数据中的信息得以保留，Ghysels等（2004）提出了一种混频数据抽样模型（MIDAS）。MIDAS模型的一个优点在于其节俭性，这意味着即使保留所有的高频数据，我们仍可以用较少的参数进行估计。

 

MIDAS模型近些年来应用十分广泛，然而大部分现有文献都只考虑平稳数据这一情况，对于非平稳数据，也只是进行简单的一阶差分后进行估计。然而对于非平稳数据，仅仅使用差分后的数据可能会忽略变量间的长期关系。

 

混频误差修正模型

 

模型应用

 

在实证部分中，作者使用该方法预测了美国的通货膨胀。被解释变量为经过季节调整的美国月度消费价格指数，解释变量选取了美国汽油价格（GAS），S&P500指数（SP），样本区间为2000年1月至2010年11月共131个样本。

 

为了检验所有可能的误差修正项是否存在协整关系，文中同时汇报了ADF检验和Johansen迹检验。

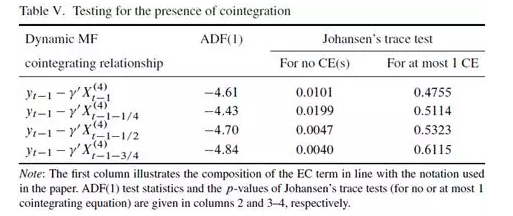
从上表可知，ADF检验和Johansen迹检验均拒绝了不存在协整关系的原假设。出于简便，作者仅估计动态协整关系为同期时的长期项。

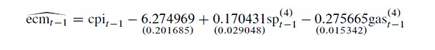
该结果表明，所有参数在任何显著性水平下均通过了显著性检验。

 

文中最后，作者用此长期项构建了误差修正模型进行预测，并与不包含长期关系的误差修正模型进行比较，作者发现该模型的RMSE在所有考虑的模型中具有最小值，表明了其优良的预测性能。

 

原文摘要

 

This paper proposes a mixed-frequency error correction model for possibly cointegrated non-stationary time series sampled at different frequencies. We highlight the impact, in terms of model specification, of the choice of the particular high-frequency explanatory variable to be included in the cointegrating relationship, which we call a dynamic mixed-frequency cointegrating relationship. The forecasting performance of aggregated models and several mixed-frequency regressions are compared in a set of Monte Carlo experiments. In particular, we look at both the unrestricted mixed-frequency model and at a more parsimonious MIDAS regression. Whereas the existing literature has only investigated the potential improvements of the MIDAS framework for stationary time series, our study emphasizes the need to include the relevant cointegrating vectors in the non-stationary case. Furthermore, it is illustrated that the choice of dynamic mixed-frequency cointegrating relationship does not matter as long as the short-run dynamics are adapted accordingly. Finally, the unrestricted model is shown to suffer from parameter proliferation for samples of relatively small size, whereas MIDAS forecasts are robust to over-parameterization. We illustrate our results for the US inflation rate.