推文人 | 李国鹏 

 

文章来源：

 

Bramoullé Y, Kranton R, D'amours M. Strategic interaction and networks[J]. American Economic Review, 2014, 104(3): 898-930.

 

一、引言

 

地理和社会联系深刻影响着个体间策略互动和经济结果。农民决定是否种植一种新的作物受到其它农民的影响，青少年抽烟和饮酒量受到其朋友圈子的影响，厂商在某地的投资决策取决于其它厂商生产互补品和替代品的情况。这些个体间复杂的策略互动，可以用社会网络来进行刻画与分析。网络经济学里面一个核心问题是：网络结构如何影响个体行为，是从网络视角上看待个体决策行为的一个突出特点（因为从定义来看，网络博弈并没有包含更多东西，也是参与者、策略和效用）。

 

这篇文章的核心贡献是首次发现均衡结果依赖于社会网络对应的邻接矩阵（下文会介绍）的最小特征值。已有的研究发现，在策略互补（strategic complements）博弈中，最大特征值很重要。但当网络中存在策略替代（strategic substitutes）时，最小特征值起着核心作用。在互补博弈中，个体间影响的方向是单调的，比如个体A提供更多的行动，个体A的邻居也会提供更多，以此类推。但是，在替代博弈中，个体间影响类似于一个涟漪——正负交替。比如在公共品博弈中，个体A提供了更多公共品，个体A的朋友就会少提供，但个体A朋友的朋友会提供更多。因此，网络上的替代博弈会相比互补博弈会带来更多困难。在这篇文章中，作者综合使用了优化、potential game和spectral graph等工具研究纳什均衡和稳定均衡，以及其和网络结构的关系。作者讨论了各种类型的社会互动——互补、替代、互补和替代同时存在，但重点集中于策略替代。因为基于策略替代的分析技术，可以方便地扩展到其他类型。

 

这篇论文还有以下的贡献，也是我比较感兴趣的内容之一：扩展了n人同时博弈并且行动空间是连续时候的情形，传统上，n人博弈局限于：（1）、所有个体都和其他个体是同等程度的互动；（ii）、对称均衡；（iii）内点均衡。这篇文章提供的工具可以研究任意可能的互动结构、更宽泛的行动空间和所有纳什均衡解（不局限于内点均衡）。作者的研究提供了新的见解，比如集中于研究对称均衡可能会失去一般性，即使个体有同质的收益函数，并且个体在网络上的位置是对称的，对称均衡可能是不稳定的，并且存在稳定的不对称的均衡。

 

作者还讨论了本文理论的三个应用：1、投资研发，在许多情形下，R&D都可以作为一种局部公共品。当公司了解了其他公司的研究结果之后，就会出现潜在的搭便车问题。在油气开采领域和农作物种植领域，都发现了类似的搭便车问题（Hendricks and Porter, 1996; Foster and Rosenzweig, 1995 ）。作者想研究的问题是，网络结构如何影响投资研发的水平和模式。2、犯罪模式，更多人加入犯罪之后，犯罪的成本会更低，但同时收益也会更低。当去掉某些链接——打掉某些犯罪联系后，一方面总的犯罪水平降低了，但是使得社会联系的作用更强了，可能会提高局部犯罪水平，作者讨论了网络结构如何影响犯罪模式。3、作者的理论研究有助于扩展有关同群效应和空间互动的实证估计，比如学生成绩如何受到其同学的影响、如何设定地区税率。作者发现经常使用的计量方法可能会错误估计这些个体间的相关性，并且在面对多种均衡的时候，作者的结果可以为减少计算复杂性提供借鉴。

 

二、基准模型

 

A.模型设定

B.均衡分析

网络是由四个个体组成的一个line。当δ<(√5-1)/2≈0.618 时，有唯一均衡，均衡时个体的actions如上图所示。当 0.618<δ<1 时，有两个均衡。其中一个均衡所有个体都是active agents，第二个均衡有一个个体是inactive agent。当 δ=1 时，有两个均衡。个体要么采取1的action，要么采取0的action。也被成为all-or-nothing equilibria。

 

C.均衡与稳定均衡

 

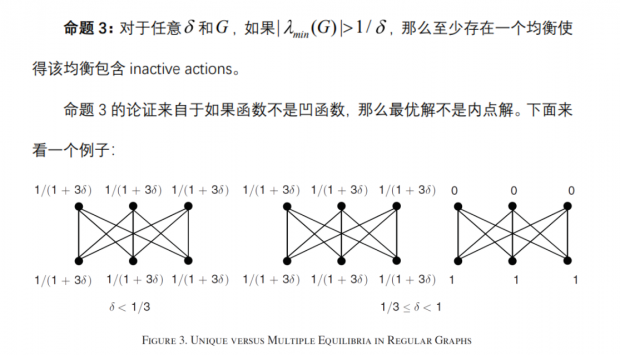
在图3是一个complete bipartite network，也就是说所有个体可以被分为两个集合，然后集合里面的个体都有三个朋友，并且三个朋友都属于另一个集合。在这个网络中，个体的地位是同质的。可以算得，λ_min (G)=-3。当 δ<1/3，即λ_min (G)<1/δ 时，有唯一均衡，即对于所有个体而言，都有 x_i=1/(1+3δ)。当 δ>1/3时，有两个均衡，分别如图3所示。这表明，即使个体的地位都是同质的，也不一定只有对称均衡。

 

接下来讨论稳定均衡（stable equilibria），稳定均衡的大概意思是：在均衡行为下，某个个体对均衡行为的微小偏离，不会导致大范围偏离。在稳定均衡中，最小特征值依然发挥了重要作用。核心发现是：如果|λ_min (G)|<1/δ ，唯一的均衡也是稳定的。如果 |λ_min (G)|>1/δ ，在可能的多个均衡中，所有稳定均衡都包含inactive actions。

 

作者研究了一种经典的关于稳定均衡的定义，这是Nash tâtonnement的连续版本。如果某个个体 偏离了均衡，其他个体会做出最优反应，那么新的向量是否依然会回到原来的均衡。考虑下面的微分方程系统：

其中，f_i (x;δ,G)是个体 i的最优反应，向量x 是系统的稳定状态（stationary state），当且仅当x 是一个纳什均衡。我们说一个均衡x是渐进稳定的（asymptotically stable），如果在 x的附近发生一个很小的扰动，系统依然会回到x 。

 

为了找到渐进稳定均衡，依然要借助于potential function。如果某个均衡是potential function的局部严格极大值，那么在均衡附近做微小的偏离，个体的调整依然会回到该均衡。也就是说，在局部没办法增加potential function的值了。但是，如果均衡不是一个严格极大值，而是一个鞍点。此时，稍微的偏离就会偏离鞍点，也就是说偏离均衡。因此，该均衡不稳定。有以下引理成立：

D.最小特征值和网络结构

 

接下来讨论网络最小特征值如何和网络结构相关。只有最近的一些数学文献考虑了网络最小特征值和网络链接结构（link structure）之间的关系，并且网络最小特征值在社会科学和物理学中还不是一个很常见的指标。

 

总体上来说，网络是更加双边的“two-sided”的时候，网络最小特征值会更大。“two-sided”意味着网络中的个体可以被划分为两个集合，集合内部的链接很少，两个集合之间的链接比较多。考虑图4的例子：

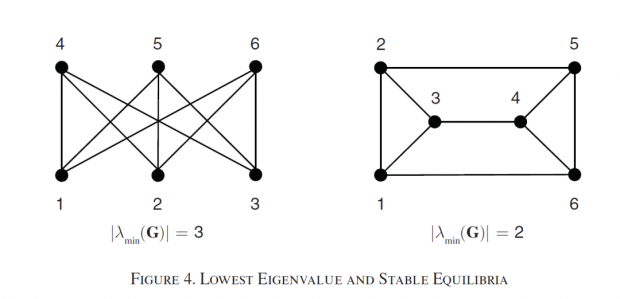
左边的网络是bipartite graph（在匹配理论里面经常使用），右边的是prism graph（棱镜网络，可能看起来比较像）。这里网络个体的数量、每个个体的链接数量都是一样的，唯一不同的是结构。左边的网络，同类个体之间没有链接，其最小特征值为-3，而右边的网络的最小特征值为-2。为了更好地考察该特征，考虑下面的最小特征值的表达形式：

第一项捕捉了 R内部的链接，第二项捕捉了S 内部的链接，第三项捕捉了两个集合之间的链接，显然，前两项都为正，而第三项为负。这个表达形式显示了为什么最小特征值捕捉了替代性。第三项在绝对值上越大，最小特征值越小，更多个体的actions向相反方向扩大。上述等式使得我们可以把一个矩阵 转化为矩阵G'，从而|l_min (G')|≥|l_min (G)|，可以通过删除 R或 S内部的链接，或者增加 R和 S之间的链接。如下列命题所示：

例如，在图4所示的网络中，对于prism network而言，我们有R={1,4,5}，S={2,3,6}。删除个体2和个体3之间的链接，可以使得最小特征值增加到约-2.22。对于bipartite network来说，已经没有办法再去增减相应的链接了，因此|-3|=3是六个个体组成的所有网络结构中可以实现的最大|λ_min (G)|。

 

有了以上的观察，我们可以回答一些有关网络最小特征值和网络结构之间的关系的问题。

 

第一个问题，给定n 个个体，什么样的网络结构可以实现最大的|λ_min (G)|，答案是一个complete bipartite graph，并且两边的个体要尽可能平均分配。命题7的直觉可以很容易扩展一下用来证明该结论，该结论被Constantine (1985)证明。

 

第二个问题，给定 n个个体和有限数量的链接，什么样的网络结构可以实现最大的|λ_min (G)|？这是一个更加困难的数学问题，Bell et al. (2008a, 2008b)的研究给予了一些启发——把个体分为两个群体，然后构成一些特殊的结构。

 

第三，我们可以精确地建立最小特征值和双边“two-sidedness”的关系吗？我们可以通过给出|λ_min (G)|的下界从而给出一些启示：下界关于两个集合内部和之间的链接成比例，也就是：

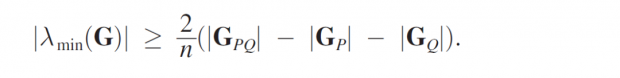
对于空网络来说，λ_min (G=0)=0，对于全连接网络来说，λ_min (C)=0。因此，随着链接增加，最小特征值的绝对值先增加后减小。但是，没办法得出链接数量和最小特征值之间的精确的关系。因为，在不同的网络结构下，可能增，可能减，也可能不单调。

 

E.比较静态分析

 

这部分讨论网络结构变化或者 δ变化如何影响均衡时的个体行为。策略替代给比较静态分析带来了挑战。考虑个体 i和个体 j之间新增加一个链接，这个链接会降低i 和 j之间采取高actions的动机，但是同时又会增加它们的朋友采取高actions的动机，以此类推。直接效应和间接效应的混合可能使得最终的结果含混不清，而多重纳什均衡又进一步加剧了分析的复杂性。

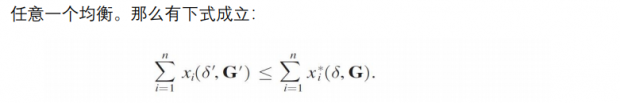
三、应用

 

A.信息创造、投资研发（R&D）和局部-全局溢出效应

 

信息和创新是私人提供的公共品的一个典型例子，这种公共品通过社交或地理联系被消费。当个体进行决策时，比如是否购买汽车或电脑、种植哪一种作物、使用哪一种药品，个体除了自己考察相关信息之外，往往也会征集来自朋友、同事或邻居的建议。在科学研究中，也涉及到试验和结果传播的问题。

 

投资研发是一个重要例子。大量实证文章考察了研发投资的溢出效应以及私人投资研发与公共收益的偏离（divergence）。在该领域，信息分享通过个体的社会联系发出。比如相似类型公司的工作者会交换相关的工作信息；在产业集聚的地方，公司之间可以通过互相学习对方的经验和教训来获益。

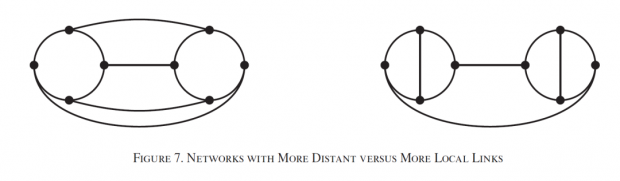
一开始有两个分离的群体，每群体有四个人（厂商），组成了一个圈。然后我们开始添加链接，在图7左边的图中，每个人都有一个链接和其他的群体相连，反映了具有远距离的信息来源，其最小特征值为|λ_min (G_a)|=3。而右边的图只有两个这样的个体，最小特征值为|λ_min (G_b)|≈2.24。当δ<1/3时，在两个网络中，创新模式相同，都集中在局部社区中；唯一的纳什均衡为x_i=1/(1+3δ)。当1/3≤δ≤1/2.24时，创新模式分化。在左边的图中，唯一的稳定结果是聚集式的创新；在右边的图中，稳定的结果混合了扩散和局部创新。总体溢出效应可以导致更集中的创新模式。

 

在农业生产中也有类似的结果。农业收成在大量发展中国家长期非常低，而其实只需要灌溉、肥料、种子改进这些简单的创新就可以大大提高收成，从而改善农民的生活情况和福利(Sachs 2005)。在针对印度“绿色革命”的研究中，Foster and Rosenzweig (1996)发现了农民在试验种子时的搭便车行为。网络和空间联系深刻影响了农业信息的传播和农民间创新的替代性（搭便车行为）(Conley and Udry 2010)。本文结果显示，局部链接的加强有助于产生更扩散的创新。

 

B.犯罪和社会网络

 

传统上，经济学家关注犯罪的动机和惩罚，但社会网络也对犯罪活动产生着重要影响，社会联系可以解释不同地区犯罪率的时间、空间变化(Glaeser, Sacerdote, and Scheinkman 1996)。Bayer, Hjalmarsson, and Pozen (2009)观察到了青少年犯罪中的同群效应。下面的例子探究了动机和社会网络如何共同决定了犯罪模式。

 

设x_i 是个体i 的犯罪水平。当社会中总体犯罪水平比较低时，个体 i的犯罪回报率比较高，这反应了对犯罪资源的捕捉。另一方面，当更多朋友参与犯罪行为时，个体的犯罪成本比较低。以贩毒为例，当贩毒的人很少时，毒品相对更之前；但是，当和自己一起贩毒的人很少时，自己的贩毒成本也会很高。个体i 的收益为：

首先，考虑网络结构的变化。考虑由G增加某些链接组成的网络G'。根据命题8，当h_ij更小的时候，网络中的总的actions水平会更高，在G中增加一些链接g_ij，会使得h_ij更小，因此会增加犯罪水平。其次，如图研发投资的例子一样，增加局部链接会导致更聚集的犯罪活动。本文还讨论了犯罪成本增加对犯罪活动的影响，主要结论是犯罪成本增加会使得总的犯罪活动下降，但是可能使得局部的犯罪的活动增加。

 

C.对同群效应和空间互动的计量估计

 

许多实证工作研究个体的活动如何受到其它个体的影响，例如某个青少年的决定取决于其朋友的决定。空间模型也经常考虑地理位置接近对经济增长、技术接纳与家庭需求的影响。标准的做法是建立一个联立线性方程组然后进行求解。

 

在某些活动中，个体的行为不能是负的，比如吸烟量或饮酒量。为了估计社会或空间互动，学者经常考虑下列的结构线性方程：

 

上面的方程有两个问题需要注意，第一个问题是个体的行动是同时被确定的，因此方程的等式右边部分是内生的；第二个问题是非负约束。第一个问题学者已经解决得比较好，但第二个问题经常被忽视。作者的贡献是，遇到多次均衡的时候，之前的研究是在估计时对所有均衡结果进行加权平均，作者指出可以仅研究稳定均衡（stable equilibrium）从而减少计算复杂度或者给稳定均衡赋予更多的权重，从而使得结果更加科学。

 

Abstract

 

Geography and social links shape economic interactions. In industries, schools, and markets, the entire network determines outcomes. This paper analyzes a large class of games and obtains a striking result. Equilibria depend on a single network measure: the lowest eigenvalue. This paper is the first to uncover the importance of the lowest eigenvalue to economic and social outcomes. It captures how much the network amplifies agents' actions. The paper combines new tools—potential games, optimization, and spectral graph theory—to solve for all Nash and stable equilibria and applies the results to R&D, crime, and the econometrics of peer effects.

 

推文作者

 

李国鹏，北京交通大学经管学院硕士研究生。对网络经济学理论与应用、数字经济、产业经济学感兴趣。邮箱guopengli@bjtu.edu.cn