推文人 | 李江艳 

原文信息：Füllbrunn, S. C., & Luhan, W. J. (2017). Decision making for others: The case of loss aversion. Economics Letters, 161, 154-156.

 

一、引言

 

在传统决策理论中，研究者通常研究的情形为决策者是其决策的唯一利益受影响者。然而，在现实生活中，也存在着这样一种情形¬，即决策者的决策不仅会影响其自身利益，还会影响他人的利益。例如，在金融市场的投资决策中，通常由理财经理代替个体投资者做出投资决策，而理财经理对于风险/损失的态度亦会直接影响其自身及客户的利益。因此，一个研究问题就此产生了。当我们在为自己做决策和为他人做决策的过程中，我们对于风险/损失的态度是一样的吗？在现有文献中， Andersson et al. (2014) 和Vieider et al. (2016) 认为人们在替他人做决策的过程中，其对于损失的厌恶程度起着关键作用。在替他人做决策时，由于损失厌恶程度的降低，人们将表现的更不厌恶风险。然而，后续研究发现这两篇文献中的结果依赖于其所使用的特定决策模型。因此，人们在为自己做决策以及为他人做决策时是否对风险有不同的态度也变成一个需要深入研究的问题。为了阐释这个问题，本文作者设计了一个经济学实验进行研究。

 

二、实验设计

 

为了研究人们在为自己做决策时对于风险/损失的态度是否与为他人做决策时有所不同，本文作者设计了如下的经济学实验。

 

1. 损失厌恶程度获取 （elicitation of loss aversion levels）

 

基于Gächter et al. (2010) 所提出的获取损失厌恶程度的方法，本文作者通过以下方法来获取实验参与者对于损失的厌恶程度。在实验中，实验者将会为每位实验参与者提供六支彩票 (lottery)，并询问实验参与者是否愿意接受每一支彩票。在每一支彩票中，实验参与者有50%的可能性赢得6欧元，亦有50%的可能性会损失2～7欧元不等 (如图1所示)。在实验结束后，实验者将从实验参与者所面临的六支彩票中随机选取一支，并据此来决定实验参与者的最终报酬。实验者使用实验参与者拒绝彩票的个数来衡量其对于损失的厌恶程度。

2. 处理 （Treatments）

 

为了更好的检测实验参与者的损失厌恶程度在为自己做决策与为他人做决策时是否存在差异，本文作者将所有实验参与者分为三组，并进行三种不同的处理 (treatments)，即为自己做决策 (Self)、为自己和他人共同决策 (Aligned)、为他人做决策 (Others)。在这三种处理中，实验参与者均参与图1中的彩票任务。唯一的区别在于：在Self 处理中，实验参与者面临的彩票任务中的表述为“… you win (lose) …”; 在Aligned 处理中，实验参与者面临的彩票任务中的表述为“… you and the other participant win (lose) …”; 在Others 处理中，实验参与者面临的彩票任务中的表述为“… the other participant wins (loses) …“。

 

同时，在Aligned 处理中，在实验参与者完成图1中任务的决策以后，系统将随机匹配两名参与者，并将其中一名参与者的决策作为相匹配的两名参与者的共同决策。在Others 处理中，系统随机选取一名参与者i 为参与者j 做决策，参与者j 为参与者k 做决策。依此类推。以上的所有匹配过程均在匿名下进行，实验参与者之间无任何互动。

 

3. 实验流程 （Procedures）

 

在实验开始之前，实验者将会大声朗读实验指导，询问实验参与者对于实验内容及细节是否有疑问并进行解答。在完成图1所示的彩票任务以后，实验参与者还将填写一个调查问卷。该调查问卷中包含关于实验参与者基本情况的问题、关于实验者风险厌恶程度的问题 (Dohmen et al., 2011) 以及关于实验者社会责任感的问题 (Berkowitz and Lutterman, 1968)。在填写完调查问卷后，实验参与者被告知其在图1所示的彩票任务中的最终报酬，并在依次被支付完实验报酬后离开实验室。

 

三、研究结果

 

1. 实验结果

 

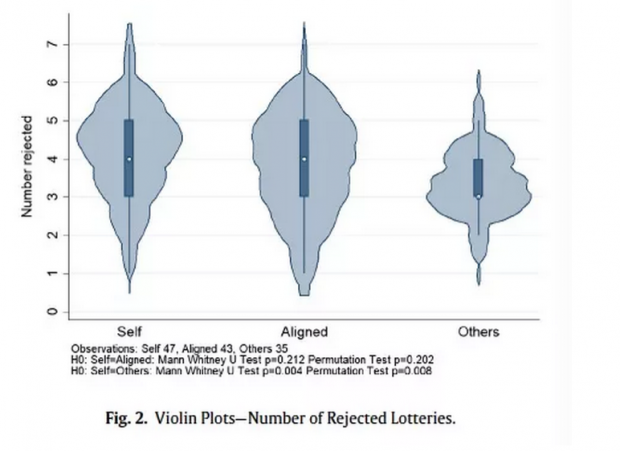
与Gächter et al. (2010)一致，本文作者仅考虑在图1彩票任务中决策为单调型 (monotonic decisions) 的参与者 (占总参与者比例为88%)。基于Gächter et al. (2010) 所提出的方法，本文作者将实验参与者在图1彩票任务中拒绝彩票的数量作为衡量其损失厌恶程度的依据。因此，实验参与者损失厌恶程度参数将被赋予7个不同等级的值 (7=拒绝所有彩票，6=拒绝彩票#1，5=拒绝彩票#1和彩票#2，… …，1=接受所有彩票)，且该参数值越大代表损失厌恶程度越高，即7代表最损失厌恶程度最高。图2显示了三种不同处理 (treatments) 下，实验参与者的损失厌恶程度及相关检验。由图2 中我们能够看出，在为自己做决策以及为自己和他人共同做决策时，实验参与者的损失厌恶程度没有显著区别。而在为他人做决策时，实验参与者的损失厌恶程度要比其为自己做决策时要低，且该结果在统计意义上显著。也就是说，人们在为他人做决策时，对损失的忍耐度要显著高于为自己做决策时。

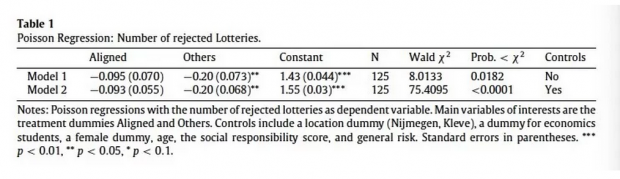
为了进一步进行检验，本文作者以实验参与者拒绝彩票数量的变量作为因变量 (dependent variable)，以代表三种不同实验处理 (treatments) 的虚拟变量作为自变量，进行了泊松回归分析 (Poisson Regression)。回归结果见下表1。从表1中，我们能够得出与图2一致的结果，即实验参与者在为自己和为自己与他人共同做决策时损失厌恶程度没有显著区别，而在为他人做决策时损失厌恶程度要显著低于为自己做决策时。

2. 累积前景理论下的损失厌恶参数

 

在本文的实验中，假设实验参与者以累积前景理论 (Cumulative Prospect Theory) 作为其决策的理论依据，则累积前景理论中的损失厌恶参数 λ 可计算如下：

 

λ=(ω^+ (0.5)×v^+ (6))/(ω^- (0.5)×v^- (L))

 

其中，在盈利领域 (+) 及损失领域 (-)内，ω代表相应的概率权重函数 (probability weighting function)，v代表相应的价值函数 (value function)，L代表所遭受损失。

 

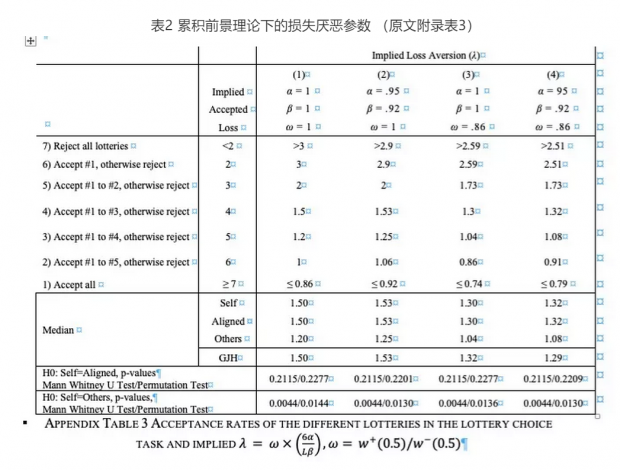
依据上式，并在考虑累积前景理论中不同的概率权重函数 ω 以及不同的敏感度 (α,β) 的情况下，本文作者计算出每种模型下本文实验中三种不同处理所对应的损失厌恶参数λ的值。计算结果如下表2 (原文附录表3)所示。从该计算结果中可以看出，在模型所取概率权重参数与敏感度参数不同时，损失厌恶参数呈现差异。但在表2所列的所有模型中均能发现在Self 处理中的损失厌恶参数显著大于在Others处理中的损失厌恶参数，即与前述实验结果一致。

 

 

四、研究结论

 

基于Gächter et al. (2010) 所提出的获得损失厌恶程度的方法，本文作者通过一个实验室实验分别对实验参与者在为自己做决策、为自己和他人共同决策、为他人决策的情况下的损失厌恶程度进行衡量，并得出结论—与为自己做决策相比，人们在为他人做决策时所表现出的损失厌恶程度相对较低；而在为自己和他人共同决策时所表现出的损失厌恶程度则并无显著差异。

 

Abstract

 

Risky decisions are at the core of economic theory. While many of these decisions are taken on behalf of others rather than for oneself, the existing literature finds mixed results on whether people take more or less risk for others then for themselves. Recent studies suggest that taking decisions for others reduces loss aversion, thereby increasing risk taking on behalf of others. To test this, we elicit loss aversion in three treatments: making risky decisions for oneself, for one other subject, or for the decision maker and another person combined. We find a clear treatment effect when making decisions for others but not when making decisions for both.