推文人 | 息晨 

原文信息：Jun Yang, Shuai Chen , Ping Qin, Fangwen Lu and Antung A.Liu, The Effects of Subway Expansion on Traffic Conditions: Evidence from Beijing. Journal of Environmental Economics and Management, 2018:88.

 

在北京生活、工作过的大家相信对北京的雾霾和堵车问题深有感受。北京车多人多，每到早晚高峰路面交通更是拥堵不堪，因而许多人倾向选择方便、准时的地铁出行。从经验判断，地铁开通一方面有助于吸纳地面人、车流量，缓解交通拥堵问题。另一方面，减少的车辆对改善空气质量或有所助益。然而，Downs定律认为城市的高峰交通拥堵总会达到道路的负载能力上限，因此长期看地铁开通等公共出行投资无助于缓解交通拥堵。但在短期，新开通的地铁会缓解交通拥堵吗？这正是本文所要回答的问题。本文使用2009-2015年间北京市6个时点、12条地铁线的开通作为准自然实验，使用断点回归设计（RDD）分析了地铁开通短期内对交通拥堵及路面行车速度的影响。

 

地铁开通背景

 

自2008年北京奥运会后，北京市政府对其地铁系统进行了扩建，2009至2014年为此投入了近200亿美元。本文新开通地铁线样本选取见表1，共包含了在6个时点开通的12条地铁线。为了使不同时点开通的地铁样本时段间无重合，选取了各开通时点前后60日作为基准分析中的时段。

 

 

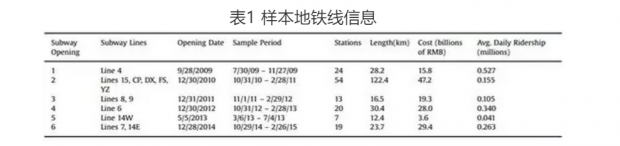
使用RDD考察地铁开通对交通拥堵影响的一个前提是相关部门不是出于缓解拥堵目的选择开通时间。作者通过阐述地铁开通的相关背景对此进行说明。首先，兴建地铁需要市政府部门将计划提前6-8年上报发改委相关机构，发改委批复同意后将在政府网站上挂出相关文件，市政府部门随后依次制订以年为单位的发展规划。由于地铁施工完成后需经过安全检验才能投入使用，加之地铁建设中各种不可控因素，提前准确确定开通时间十分困难。此外，地铁建设是重要的政府工程，需要政府领导班子如市长、市委书记等到场出席开通仪式，因此需协调政府领导的时间，相关部门不太可能是为缓解交通拥堵确定开通时间。

 

数据与实证设定

 

本文的RDD基准模型设定如下：

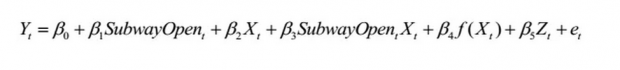
其中Yt为t日反映交通需求的相关变量，在本文中包括总地铁客流量、开通前已存在的地铁客流量、公交车客流量、总交通拥挤指数、早高峰交通拥挤指数、晚高峰交通拥挤指数。SubwayOpent为代表t日是否开通了新地铁的二值变量，其系数β1为本文主要关心的估计量。Xt为时间趋势变量，当t日有新地铁开通时其为0，早于t日则其为负值，t日后为正值。f(Xt)为k阶多项式函数，用以控制无地铁开通时交通需求的变化，在基准分析中选取k为3。Zt为一组控制变量，包括周几（Day of Week）虚拟变量组、t日北京市限号虚拟变量组、地铁线虚拟变量组、是否是极端天气的虚拟变量组，其中极端天气包括热浪、寒潮、暴雨与大风雪。考虑到周末与节假日的出行居民人数可能异于工作日，在分析中删去了此部分样本。最后，作者将标准误聚类到周几×当日限号号码层面，在后续的稳健性分析中作者尝试了多种类型的标准误形式。

 

本文使用的反映交通需求的变量来自北京市交通运行交通监测调度中心发布的每日监测数据，除地铁与公交日客流量外，还包括根据官方标准测度道路拥挤程度计算的每日交通拥堵指数（TCI），可通过相应的对应关系实现TCI与通行时间间的转换。此日值数据集时间跨度为2009年1月至2015年5月，涵盖了表1中基准分析的样本时段。

 

为考察地铁开通对道路通行速度的影响，作者获得了2014.9.1-2015.3.31间日层面的22条道路的早高峰通车速度与晚高峰通车速度数据，可籍此分析地铁7号线与14e号线开通对道路通车速度影响。

 

实证结果与稳健性检验

 

（一）基准分析结果

 

表2展示了RDD的基准分析结果。

 

 

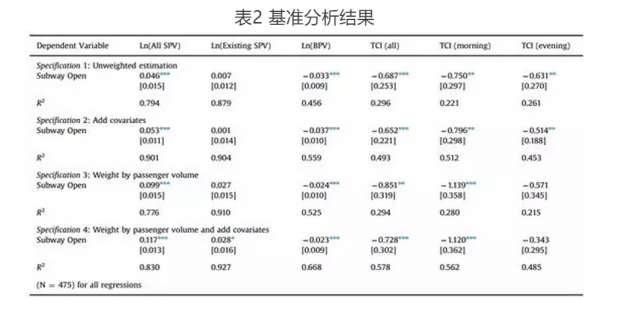
模型1未加入控制变量Zt，简单分析了地铁开通对各交通需求变量的影响。模型2中加入了控制变量Zt。由于不同新开通的地铁线对交通需求的影响不同，客流量较大的地铁线会对交通产生较大影响，作者在模型3与模型4中以各新开通线的平均客流量作为权重进行加权。模型3中未加入控制变量Zt，模型4中加入了Zt。我们主要关注模型4的估计结果。

 

由表2可见，新开通的地铁将显著增加总地铁客流量，但不会对已存在的地铁线客流量产生显著影响。地铁开通也使乘公交出行的人数减少，反映了地铁与公交间的替代性。在主要关心的地铁开通对道路拥挤的影响中，发现地铁开通减少了总拥挤指数与早高峰拥挤指数，但其对晚高峰道路拥挤程度的影响是不显著的。进一步结合TCI的定义，可计算知表2模型4中对总TCI的估计系数-0.728对应日均通行时间15%的减少，意味着地铁开通在短期内相当程度地缓解了北京市道路拥堵情况。

 

（二）地铁开通对道路通车速度的影响

 

使用22条道路的早高峰与晚高峰道路通车速度数据，作者以图1展示了地铁开通对周边道路通车速度的影响。

 

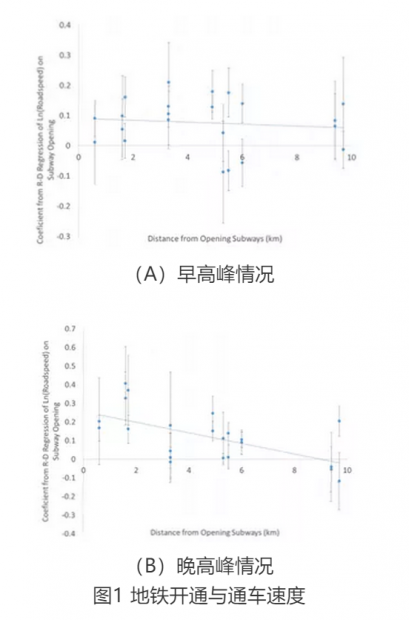
上图中每个圆点代表了类似基准模型设定的点估计结果，其中被解释变量为每日早高峰/晚高峰通车速度的对数。x轴代表各道路中点至7号线/14e号线的距离。图1反映出地铁开通对周边道路通车速度具有促进作用，与前述基准分析结果一致。但随着地铁线与道路距离的增加，此种作用呈现出衰减特点，且晚高峰时段较早高峰时段衰减更甚，这为基准分析中地铁开通不显著影响晚高峰TCI提供了一种解释。

 

（三）稳健性检验

 

（1）扩大样本量。为使各时点开通的地铁线匹配的样本区间无重叠，作者在基准分析中将时间范围设定为开通前后各2个月。在删去4号线与5号线后，可将样本跨度增加至6个月，文中选取了各种时间跨度进行了与基准分析类似的分析。

 

（2）节假日的影响。表1中各地铁线的时点部分在节假日附近，如元旦。尽管在分析中作者已剔除了节假日样本，但居民在节假日的提前离京或晚归情况仍可能对交通运输需求产生影响。作者进一步提剔除了节假日首尾3日的样本，因为提前离京或晚归通常发生在此时期内。

 

（3）安慰剂检验。设定了可与表1匹配的月、日时点进行安慰剂检验，但其对应的年无地铁开通，具体时点设置请参见原文。

 

（4）北京实行的出行政策的影响。北京在2011年1月起实行的机动车摇号政策及2013年6月实行的出租车调价政策或影响分析结果。作者删去表1中时点2与时点5开通的地铁样本进行了再分析。

 

（5）分析结果是单一地铁开通时点导致的。分别移除了6个时点中的1个时点样本，使用剩下的5个时点样本进行再分析。

 

（6）出行的季节性特征影响了分析结果。在分析中加入了周固定效应。

 

（7）使用多种阶数的多项式函数。

 

（8）使用多种类型的稳健标准误形式。

 

以上各稳健性检验结果均与基准分析结果高度一致，表明地铁开通在短期可减少地面拥堵的结论是稳健的。

 

结语

 

本文中，作者使用高铁开通作为准自然实验，使用RDD考察了高铁开通对地面拥堵的影响。但限于RD分析的外部有效性，此文仅提供了短期内的结果，并未解释或反驳长期情况的Downs定律。

 

Abstract

 

Does public transportation reduce vehicle congestion? Using a regression-discontinuity framework, we examine the effect of six subway openings on short-run congestion in Beijing between 2009 and 2015. We find that vehicle congestion drops sharply immediately after new subway openings. In our central specification, each of the subway openings decreased delay times by an average of 15% in the short run over the city of Beijing.