推文人 | 杨冬 

文献来源：Jondeau, E. and Rockinger, M. (2006), Optimal Portfolio Allocation under Higher Moments. European Financial Management, 12: 29-55. doi:10.1111/j.1354-7798.2006.00309.x

 

研究介绍

 

众所周知，金融市场收益率数据往往是非正态的，大量的经验研究表明收益率数据分布具有厚尾和非对称性。正因如此，在财富配置方面基于马科维兹（1952）的均值-方差准则适当性受到众多质疑。部分学者考虑采用高阶函数去近似期望效用函数（Arditti,1967;Levy,1969;Samuelson,1970）。但早期关于高阶矩有用性的研究成果结论并不统一。

 

近些年来，计算机的发展使得基于高阶矩的投资组合优化得到了进一步的发展。如Lai（1991），Chunhachinda et al.（1997）和Prakash et al.（1997）使用多项式目标规划方法对包含偏度的投资组合选择进行了研究。所有研究均表明包含偏度的投资组合可以显著提高收益。另外一种处理高阶矩的方法是使用泰勒展开获得期望效用函数的近似估计。本文中，作者系统研究了在投资者希望期望效用函数最大化条件下非正态收入如何影响财富的最优配置。

 

最优投资组合配置

 

我们假定投资者配置资产的最终目标是期末财富W的期望效用最大U（W），并假定初始财富为1。有n个风险资产的收益向量可表示为R=(R1,…Rn)`。在不能存在无风险资产和不允许做空的条件下，最优配置问题可以表述为如下形式

 

可以发现，期望效用函数取决于期末财富分布的各阶中心矩。

 

由于无限阶的泰勒展开在运算中无法实现，其中一个解决方法是通过给定截断阶数以获得其近似结果。例如，标准的均值方差准则是在k=2处截断。然而，在何处截断最优仍然没有更好的选择方法。Hlawitschka（1994）发现，即使在无限展开时收敛，在给定阶段阶数时添加更多的项仍会恶化渐进效果。由于四阶矩具有较好的经济意义，作者在4阶处做了截断，可得

 

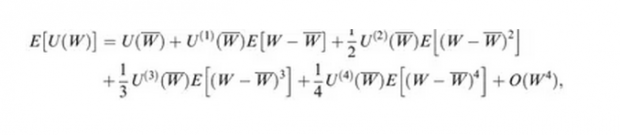
经验分析

 

在经验研究部分，作者为了研究收益率与正态分布差异大小对投资组合影响的不同，分别采用了三种数据。第一类是以美元计价的北美、欧洲和亚洲股票市场周度数据，该数据与正态分布较为接近；第二类数据为标准普尔100指数周度数据，部分数据与正态分布相差较远；第三类数据为以美元计价的新兴市场国家月度数据，该数据往往具有显著的非正态特征。关于数据采集的具体情况如下表1所示：

 

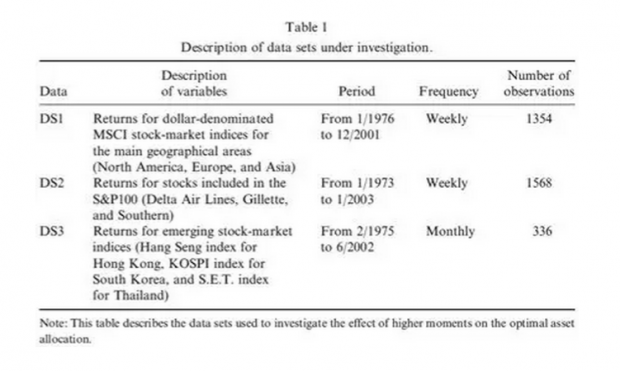
在文中，作者还对三类数据的各阶矩以及正态性做了详细的计算和检验。结果发现，所有数据均拒绝了正态分布的原假设。为了进一步分析三种数据下投资者对于资产配置的差异，文中作何分别计算了基于直接优化方法以及泰勒展开时投资组合权重，以及机会成本。以第一类数据为例，研究发现基于直接优化方法和在不同阶数泰勒展开方法计算的最优配置权重差异不大，采用范数以及机会成本计算的差异也显示出同样的结论。

 

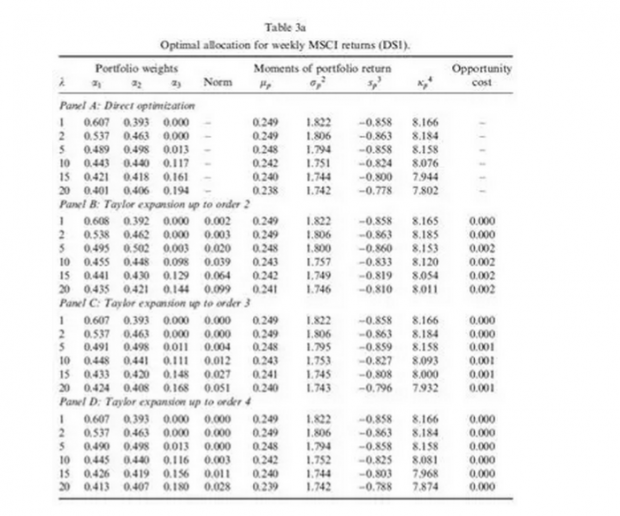
然而，当数据与正态分布差异较大时，这一结论便不再成立。此时将高阶矩信息考虑到投资组合中可以显著降低交易成本，同时采用L1距离计算的结果与优化结果更为接近，此处我们列出使用新兴市场国家的结果。

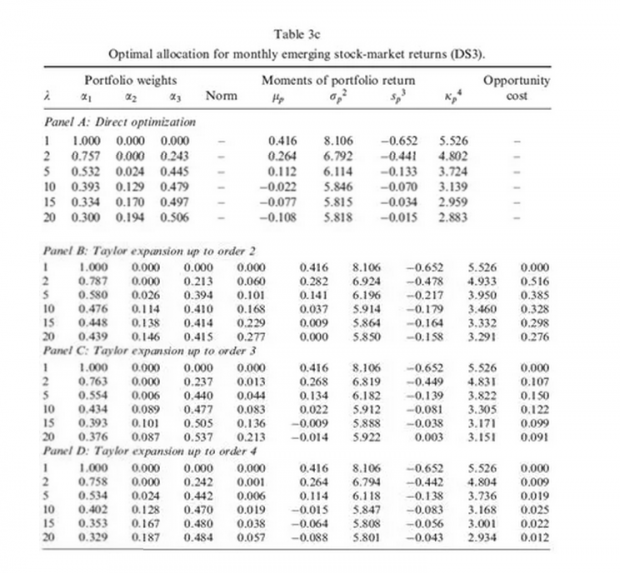
结论

 

本文作者主要研究了如下两个问题并得出了有益的结论：第一，在期望效用函数框架下非正态性对于资产配置的影响。第二，与非正态的差异是如何基于效用函数下最优配置的。

 

Abstract

 

We evaluate how departure from normality may affect the allocation of assets. A Taylor series expansion of the expected utility allows to focus on certain moments and to compute the optimal portfolio allocation numerically. A decisive advantage of this approach is that it remains operational even for a large number of assets. While the mean-variance criterion provides a good approximation of the expected utility maximisation under moderate non-normality, it may be ineffective under large departure from normality. In such cases, the three moment or four-moment optimisation strategies may provide a good approximation of the expected utility.