推文人 | 王彦锋

 

原文信息：Weiming Li, Jing Gao, Kunpeng Li & Qiwei Yao (2016).  Modeling Multivariate Volatilities via Latent Common Factors, Journal of Business & Economic Statistics, 34:4, 564-573, DOI: 10.1080/07350015.2015.1092975

 

摘要

 

波动率（以条件异方差的形式呈现）在各种金融业务（包括资产定价，投资组合的分配，期货的套期保值）的控制和风险预测中起着重要的作用。然而，建立和预测多维条件异方差面临着技术上的挑战。借助于一些共同的和潜在的因子往往会对许多金融资产的波动产生影响,本文提出了一种降维方法来建立多元波动率过程，该方法通过估计一个低维的空间（波动率空间）来估计多元波动率的动态性。该方法可归结为是对非负正定矩阵的特征分析，它实施起来是简单的。因此尽管对于数以千计的资产建立模型时，该方法也是适合的。另一方面，该模型也可适用于估计多维过程的复杂条件异方差。本文给出了该方法的渐进性质并进一步通过使用模拟技术以及真实的数据来说明该方法。

 

一、引言

 

波动率是对资产收益率风险以及不确定性的测量，它通常被定义为在给定当前时刻所有可用的信息下，资产收益率的条件标准差。对于波动率恰当的设定以及预测在金融领域的重要性不言而喻。虽然目前对于单变量波动率的统计模型，相关的推断方法以及理论发展的相当成熟，但是现实中，我们往往要对多变量的波动率进行分析。对于建立多元波动率模型，当维数较高时，面临着的一个挑战是维数灾难的问题，即随着资产个数的增加，方差协方差矩阵待估参数将急剧增加，从而给统计推断带来困难。

 

金融领域有一句俗语：“市场是一起行动的”，这句话反映了一个事实，即金融领域的一些资产的价格以及他们的波动率被一些少量的相同的因子所影响。这在著名的资产定价模型和Fama–French模型上有所体现。本文提出了一种简单的方法来识别这些潜变量的共同的因子，并用这些潜变量共同因子来估计多元波动率。

 

二、方法

 

三、蒙特卡洛模拟及实证分析

 

文章模拟了四个不同的例子，分别涉及到从低维到高维，以及存在厚尾的情况。对于每一个例子，本文比较了文中所提出的方法与Hu and Tsay (2014)所提出的PVC方法的估计结果。在给定其他条件不变的情况下，本文研究了对于不同m的取值，对于估计结果的影响，结果发现对于m的选择，并不会对估计结果产生大的影响。通过对比四种不同例子两种估计方法估计的结果，我们可以发现我们的方法估计效果都要优于PVC方法。

 

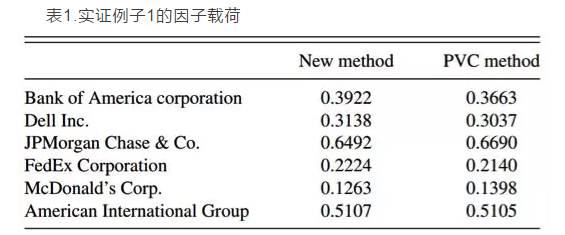
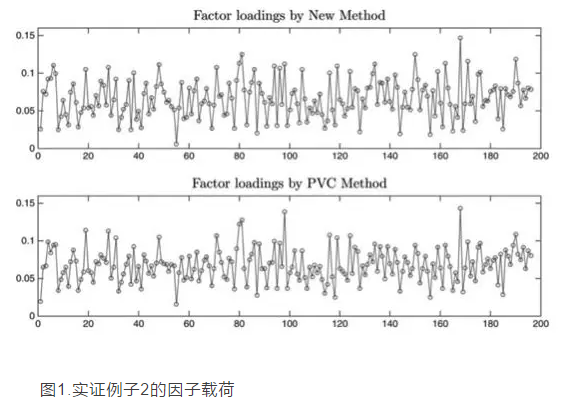
本文通过两个真实的例子来说明所提出的估计方法的估计效果。第一个实证例子是六只股票的日收益率，时间区间为：2002年1月2日到2008年7月10日。第二个实证例子是从S&P500指数里面选择196只股票日收益率，时间区间为：2009年7月13号到2014年7月11号。对于两个例子，通过公式（7），都得到r=1，两种方法估计得到的因子载荷基本相同，表1给出了第一个例子两种估计方法得到的因子载荷的结果，图1给出了第二个例子两种估计方法得到的因子载荷的结果，两种估计方法得到的因子载荷的相关系数分别达到了0.9993和0.936.

结论

 

本文提出了通过使用潜变量因子来估计多元波动率模型的方法，因为该方法是基于非负正定矩阵的特征分析，因此该方法适用于成千上万维度的变量。它可以被看作Hu and Tsay (2014)所提出的PVC方法一般版本。该方法施加很少的矩条件，并且在处理对于新息项存在厚尾的情况更有效。

 

ABSTRACT

 

Volatility, represented in the form of conditional heteroscedasticity, plays an important role in controlling and forecasting risks in various financial operations including asset pricing, portfolio allocation, and hedging futures. However, modeling and forecasting multi-dimensional conditional heteroscedasticity are technically challenging. As the volatilities of many financial assets are often driven by a few common and latent factors, we propose in this article a dimension-reduction method to model a multivariate volatility process and to estimate a lower-dimensional space, to be called the volatility space, within which the dynamics of the multivariate volatility process is confined. The new method is simple to use, as technically it boils down to an eigenanalysis for a nonnegative definite matrix. Hence, it is applicable to the cases when the number of assets concerned is in the order of thousands (using an ordinary PC/laptop). On the other hand, the model has the capability to cater for complex conditional heteroscedasticity behavior for multi-dimensional processes. Some asymptotic properties for the new method are established. We further illustrate the new method using both simulated and real data examples.