推文人 | 余颖丰

 

原文信息：Markus K.Brunnermeier, Yuliy Sannikov,“Marco, Money and Finance: A Continuous Time Approach”,NBER Working Paper No.22343,June 2016.

 

一 摘要

 

宏观经济学和金融学如今视乎已是两个不太相关的学科，但是在宏观经济学诞生之初，凯恩斯等人却是希冀于研究宏观变量和金融系统稳定之间关系而产生出来的学科。为何两个学科分道扬镳？两个已经“分手“超过半个多世纪的学科还能否重新牵手，再续前缘？请看本文为各位娓娓道来。今天的推文主人公是以下这位斯坦福大学的Yuliy Sannikov教授，他是2016年克拉克奖得主。

新的数学方法总会对我们研究宏观经济与金融问题提供新的视角和新的思路。本公众号也介绍了大量的宏观经济与金融的前沿文献和书籍，但大多数文献都是基于DSGE（动态随机一般均衡视角）。诚然，DSGE是目前研究宏观经济与金融的主流方法论和分析框架，但是它本质上也有非常多的局限性，比如DSGE模型都是事先假设系统各个变量存在稳态，模型几乎不能考虑多均衡问题。而现实中的金融系统往往存在多均衡情形。DSGE在假设存在稳态后，会对变量进行对数线性化处理，这样的好处有非常多，尤其是在对模型的参数估计时，这种便利就变得非常明显，因为我们可以借用强大和可靠的卡尔曼滤波技术。当然如果要处理非线性DSGE模型，这就需要利用粒子滤波器，这就会使得参数估计变得异常繁琐，此外粒子滤波器理论本身也有很多问题，比如粒子退化现象等问题，而我国的宏观经济数据质量都是参次不齐而且不少重要经济变量数据还存在缺失，因此使用粒子滤波器进行DSGE参数估计都可能使最终效果大打折扣。由此可见，在我国利用DSGE的非线性化之路研究我国问题或许会走得非常坎坷，而如果我们继续使用对数线性化方法，也存在严重问题，因为我们都知道很多重要真实经济变量，比如消费是存在二阶矩的统计特性的（审慎性储蓄问题）而资产价格的收益率更是有明显的肥尾、波动聚凝等非线性统计特性。此外，DSGE往往仅能研究某冲击对经济变量的持续性和放大效应，而随机冲击的新息仅能做独立同分布的正态分布假设（虽然有学者尝试采用t-分布，但是这些改良都有可能困难重重）。一个主要的原因是DSGE理论采取离散时间系统，而有学者认为采用连续随机系统应该可以较好的同时解决以上问题。

 

目前已有国外学者采用连续随机方法研究宏观金融与经济问题，2016年克拉克奖得主Yuliy Sannikov等人就采用了这样的方法。该文章更像是教科书式的指导建模建议，该文章指出利用他们提出的建模分析方法可以研究：宏观变量的动态均值和动态风险问题，可以考虑和研究尾部风险（通过随机波动率模型）和危机概率发生之间的关系、内生杠杆率问题、资本不足（undercapitalized）问题、时变的风险溢价问题、外部融资溢价问题，此外基于他们提出的思路还可以考虑现在出现的波动率悖论问题以及凯恩斯时代的审慎悖论问题。

 

二 宏观经济与金融的历史传承

 

Sannikov文章的理论贡献也十分明显，他在第二章讨论了宏观金融与经济研究的历史传承问题，而他从事的工作其实是统一了宏观经济与金融问题，将这两个问题纳入到统一的分析框架中。具体可见下图。

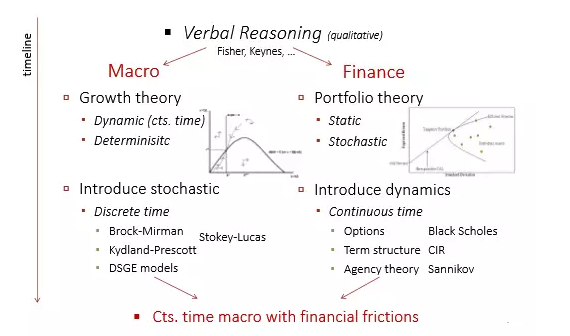
Sannikov指出宏观经济学是诞生于上世纪30年代“大危机“时代的产物，在大师辈出的时代（比如：费雪大战凯恩斯）宏观经济与金融稳定本是一体讨论的问题，但是后来宏观经济学和金融学开始分家。宏观经济学家开始将精力集中在研究经济增长理论，这也就是经济系学生们熟读罗默的《高级宏观经济学》后印象最深刻的比如是经济增长理论，学完罗默的教材基本不知现代金融理论为何物，因为罗默的教材并没有一张专门讲资产定价。Sannikov认为从研究经济增长理论开始，宏观经济学研究进入基于连续时间函数+确定系统的时代。随着真实周期理论的兴起，“淡水”派的出现，再到后来“咸水派”新凯恩斯主义的大行其道，这也就是大家所知道的---NK-DSGE成为主流，宏观经济学研究成了主要基于离散时间+随机系统。至于DSGE分析框架的缺陷前面我们已聊过了。

 

而金融学却走上了另外一条道路，金融学开始关注微观个体的投资决策问题，其后金融数学与金融工程学(也就是现在的量化金融学)的兴起，给金融学领域带来了强劲的数学武器---随机分析（stochastic calculus）。Sannikov觉得是时候让宏观经济与金融重新融合在一起进行研究，也就是宏观经济学可以研究金融系统稳定性问题，当然反之亦然，而且这一切都可以基于随机连续时间方法下进行，而且完全不“违和”，可以做到美丽的统一。

 

三 简论Sannikov的“四步法”

 

Sannikov从第二部分开始介绍了他的基于随机连续时间方法的分析框架，主要是分为四步，我们将其简称为“四步法（The Four-Step Approach）”。作者首先举了一个简单模型。然后举了一个含价格效应和系统不稳定的模型。最后举了一个含货币的模型为例。

 

现仅将思路简单描述如下。

 

 

（一）模型的基本假设

 

有两个个体：专家(experts)和家庭(households)。

 

专家可以持有风险资产，而家庭不可以持有风险资产。

 

家庭可以购买无风险资产，等于是按无风险利率贷款给专家。

 

无风险利率并非外生，其设定如C-CAPM理论，由消费的均值和消费的波动率所决定。

 

专家不能发行风险资产。专家对风险资产融资仅能通过发行无风险债券进行。

 

个体都是价格的接受者，都是市场价格的接受者，市场不存在噪音型交易者。

 

3.寻找财富分配比率变量ηt的运动方程。运动方程本质上指的是要找出某变量的微分方程形式。当然在简单模型中这一步较为简单，因为此时q是一个常数，但是在其他扩展模型中，这一步骤还是比较复杂，

 

4.找出重要变量关于ηt的运动方程。我们会关注宏观经济与金融系统的若干变量，比如我们会关注资产价格qt的运动，我们会关注无风险利率rt受消费水平或消费波动率影响的动态变化，那么我们最后一步的目的就是要找出这些我们关心的变量的运动方程，我们要让我们关注的这些变量是关于财富分配变量（整个系统中，最重要的一个状态变量）ηt的运动方程，这就是第四步的目的！！！

 

当然找到所有的方程后，最终要解出以上微分方程，Sannikov推荐了两种解法，一种是The Shooting Method，另外一种是The Iterative Method。

 

Abstract

 

This chapter puts forward a manual for how to setup and solve a continuous time model that allows to analyze endogenous (1) level and risk dynamics. The latter includes (2) tail risk and crisis probability as well as (3) the Volatility Paradox. Concepts such as (4) illiquidity and liquidity mismatch, (5) endogenous leverage, (6) the Paradox of Prudence, (7) undercapitalized sectors (8) time-varying risk premia, and (9) the external funding premium are part of the analysis. Financial frictions also give rise to an endogenous (10) value of money.