推文人 | 靳晨鑫 

 

原文信息：Chang-Tai Hsieh, Peter J. Klenow，Misallocation and Manufacturing TFP in China and India，The Quarterly Journal of Economics, Volume 124, Issue 4, November 2009, Pages 1403–1448.

 

原文链接：https://doi.org/10.1162/qjec.2009.124.4.1403

 

01问题引入

 

根据大量的现有文献研究的结果显示，穷国与富国之间在生活水平上的差异在很大程度上可以归因于国家间全要素生产率(TFP)的不同，根据基本的索洛增长模型，全要素生产率是除要素投入外决定产出的重要因素。于是自然而然地，本文作者关注的问题是国家之间全要素生产率的巨大差别是从何而来的。

 

以往关注全要素生产率国家差异性的文献大多着眼于生产技术的扩散。Howitt (2000) 和Klenow & Rodriguez- Clare (2005)的文献都说明了从发达国家到欠发达国家之间的技术外溢较慢是造成全要素生产率出现较大国家差异的重要原因，但是Restuccia & Rogerson (2008)的文献首次关注了企业间的要素错配(resources misallocation across firm)对于一国全要素生产率的重要影响。有关要素错配，作者举了一个简单的例子，假设有两家制造业企业（企业A与企业B），除其中一家和政府联系较为紧密（企业A）外两家企业完全相同，由于同政府的联系较紧密，企业A在获取贷款时的利息更低，根据边际成本等于边际收益的均衡条件，企业A的资本边际产品更低，资本的边际生产力也就更低，如果将企业A获得的资本专业给企业B，那么社会总产出就会增长，而社会的全要素增长率就会上升。上述的简单例子就说明了企业之间资源错配（政府的联系在资本的企业间分配中打入了一个楔子，造成了扭曲）对于社会全要素生产率的负面影响。而根据McKinsey Global Institute (1998)和Lewis (2004)的案例研究也为上述的案例提供了现实证据。巴西对于零售业部门劳动力市场的管制使得大型超市（沃尔玛等）雇佣劳动力的成本上升，而当地非正规小型零售企业可以轻松地逃过劳动力管制而获得较多的廉价劳动力，这样使得在巴西更为有效率的企业没有办法获得足够的劳动力而无效率部门获得了对于的劳动力，降低了巴西零售业的发展潜力与效率；此外，各国企业均有着不同的政治联系、获得补贴贷款和寻租的空间，这些都为资源错配说的成立提供了基础。Restuccia & Rogerson (2008)关注了要素错配对于全要素生产率的影响，而H&K则在此基础上认为各国要素错配的程度不同，进而成为了各国全要素生产率存在差异的原因，本文的目的之一即为要素错配影响总全要素生产率(aggreagate TFP, sector-level TFP)提供定量的证据。

 

本文的具体结构为：首先通过理论模型构建更高的扭曲（distortion，用来衡量前文的resources misallocation的程度）和更低的总全要素生产率之间的联系；其次使用中国、印度和美国制造业企业级的微观数据对理论模型的参数进行估计，具体估计扭曲的大小和总全要素生产率的值，分析扭曲和总全要素生产率的国际差异；将中国和印度的要素扭曲程度降至美国的水平进行反事实分析，研究中印两国降低要素扭曲程度后总全要素生产率的变化和增长。而作者选取中国、印度与美国作为研究对象，其中以美国作为基准，主要是由于美国一般意义上是制度最好的国家；而中国和印度由于经济体量大，近些年的经济增长速度也较为显著，作者认为中印两国相较于其他国家具有更好的代表性，但经后文更深入的分析可知，美国作为基准也有更深层次的问题，作者将美国更

 

准确地定位于critical benchmark（测量误差等等多方面的因素）。

 

而本文的结论为，当中国和印度的扭曲程度下降至同美国同一水平时，中国的总TFP将增长30%到50%，而印度的总TFP将增长40%到60%。

 

02模型推导

 

本文构建了一个基于异质性企业和垄断竞争的十分标准的模型（没有考虑国际贸易的Melitz模型），但在本文模型的具体理解上仍旧有一些困难：首本文模型的主要框架有三层的生产函数构成，和我们之前阅读过的结构方程模型从效用函数到生产函数闭合的范式略有不同，其次本文的模型和推导中有很多错误和没有用的公式，给阅读理解带来了困难。但其实本文模型也是一个闭合的模型，因为对于最外层生产函数（最终产品部门）隐含了U = Y形式的生产函数（并不局限于此形式，“越多越好”的生产函数形式均可）；此外，上游产品的生产函数其实对于下游产品（中间产品）是隐含的效用函数。当明确这两点后，本文的模型就从纯生产部门的模型变成了一个闭合的结构方程模型。具体的建模思路为，明确各层生产函数的形式并求解各层生产函数的价格指数（便于模型的求解和后续参数估计）)引入企业级的扭曲)求解扭曲同总TFP之间的关系。本文的模型假设生产函数有三层，最外层生产函数生产最终产品Y并在完全竞争的市场上销售，第二层生产函数生产上游中间产品Ys并在完全竞争市场上销售，最内层生产函数生产下游中间产品Ysi并在垄断竞争的市场上销售。

 

 

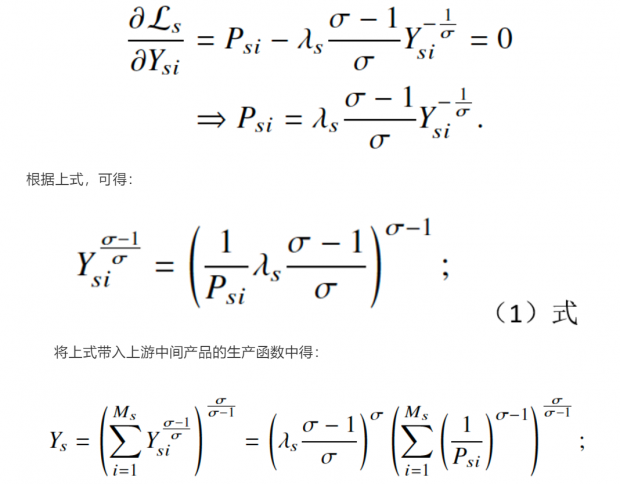
根据上式和模型的其他部分，我们可以得知基于本文模型假设下隐含的初步结论：

 

（1） 当两类要素扭曲τYsi和τKsi均为零时，即便各企业的TFPQsi不同，各企业的TFPRsi则是严格相同的（造成这一差异的原因是高物质生产力的企业面临的市场价格更低），这也是本文实证部分的重要基础，需要通过各企业TFPRsi的不同量化各企业的要素扭曲水平；

 

（2）对于TFPQsi和TFPRsi的区分对于参数估计部分尤为重要，因为数据库中各企业的产品产量使用美元计数(PsiYsi)而不是实物计数(Ysi)，使用TFPRsi作为企业级的全要素生产率衡量在实证部分更为方便；

 

（3）当企业面临更高的TFPRsi表示企业面临的要素扭曲或阻碍更大（所以对于企业级TFP来讲，更大的TFPRsi可能并不是一件好事，因为决定总TFP的是TFPRsi的整体分布而不是某一个取值，而行业级TFP（即总TFP）同最终产品的产出数量才是正相关关系），这意味着面临要素扭曲的企业的规模小于其最优规模。TFPRsi的企业应该获得更多的资本或劳动力直至实现TFPRsi的均等化，这样意味着可以在更低的价格下产出更多的产品。

 

 

其中TFPRs是行业级资本和劳动力的边际收益产品的几何平均数。（3）式是本文参数估计的核心方程。对于TFPRs的完整决定式，首先需要明确行业级资本和劳动力的边际收益产品的决定式：

 

 

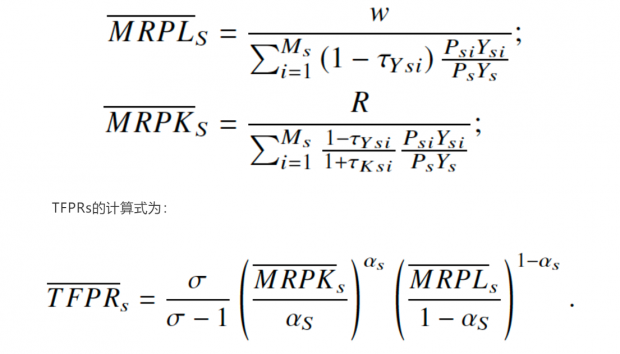
6.潜在结论

 

A. 当 σ> 2时，Asi的方差越大则TFPs越大:

 

（1）当要素扭曲水平不变时，Asi更高的企业MC更低，从而面临的价格指数Psi更低;

 

（2）TFPs类似于由Asi加权得到，根据TFPRs的计算公式可得，当Asi的方差变大时，使得较大的Asi计算权重越大，所以Asi的方差越大，则TFPs越大。

 

B. 当 σ> 2时，TFPRsi的方差越大则TFPs越小:

 

（1）当Asi水平不变时，更高的TFPRsi是由于更高的价格指数造成的，同时也意味着更高的扭曲程度；

 

（2） 更高的要素扭曲程度意味着计算TFPs时的权重更小，所以TFPRsi的方差越大则TFPs越小。

 

03数据

 

原文中对于数据的声明极其语焉不详，本文在此对于数据结构和具体内容不再进行介绍，仅着眼于对参数估计部分有直接重要意义的内容。就数据库而言，印度的四分位行业企业数据来自于印度1987-1994年度(会计年度)的ASI数据库，中国的数据来自于1998-2005年度的工业生产年度调查(Annual Surveys of Industrial Production)数据库，而美国的数据则来自于1977、1982、1987、1992和1997的以五年为统计周期的制造业普查(Census of Manufactures)和制造业年鉴(Annual Surveyof Manufactures)数据库。根据数据库，我们可以直接获得的数据包括：w、PsiYsi、Ksi、Lsi。而出于方便的考虑，本文对于模型中的一些关键参数进行了直接设定：设定资本收益率R=0.1（其中实际利率为5%，折旧率为5%）；而对于下游中间产品的替代弹性ɑ，作者将其设定为3（这一假设实际非常温和，根据后续的稳健性检验可知，替代弹性的值越大，降低要素扭曲时的总TFP增长越多，而根据相关文献例如Broda & Weinstein (2006)和Hendel & Nevo (2006)的实证结果，替代弹性的大致取值范围为从3-10，本文将设定为3不会夸大最终的实证结果）；而根据CM/ASM数据库的数据结构，作者定义资本份额数据为 ，其中ɑUSst可直接从数据库中获得。对于最外层的最终产品生产函数，作者在参数估计处理上将最终产品设为计价物(P = 1)，所以我们不需要_x0012_θS的数据。

 

04实证结果与反事实分析

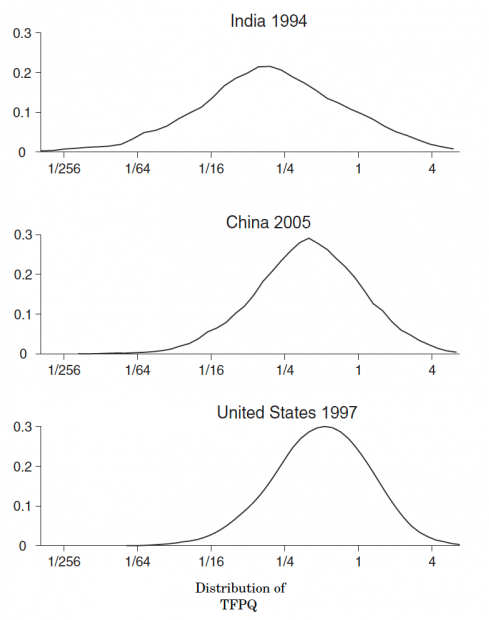
上图的结果为每个国家最后一年TFPQsi拟合值的分布。相较于中国和美国，印度TFPQsi分布的方差更大，而中美的TFPQsi分布形状类似。但中国的TFPQsi分布可能是由于数据结构造成的，因为中国的工业生产年度调查数据库只调查了一小部分的私有企业，这会造成数据的偏差，所以印度和美国的数据更具有可比性。

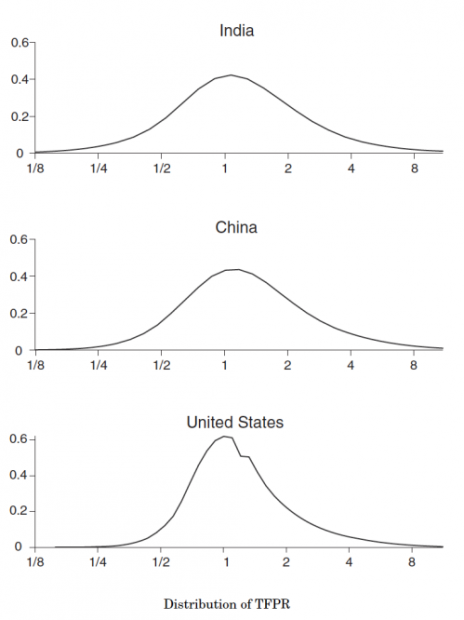
上图的结果为每个国家最后一年TFPRsi拟合值的分布。显而易见的是，印度TFPRsi分布的分散程度比美国的更大，即便中国所使用的数据库涵盖了较少的私有企业，中国TFPRsi的分散程度仍旧明显大于美国。此外，根据图中坐标刻度可知，中美印三国TFPRsi的均值相差无几，根据前文模型的结论，TFPRsi的方差更大，TFPs即总TFP越大，上图的结果也隐含了美国的总TFP大于中印两国，这与一般认识相同。

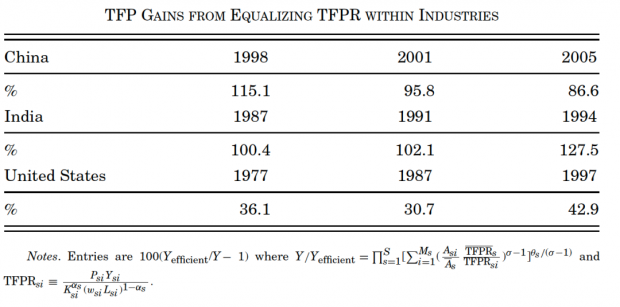
接下来作者开始进行多个反事实分析。上图对应原文中的表IV，现实的是当中美印三国均将两种要素扭曲降至零时总TFP的变化百分比。可以看出，中美印三国在消除资本扭曲和产出扭曲时总TFP都有较大的增长，这说明在这三个国家中，都存在明显的要素扭曲；而美国的总TFP收益小于中印两国，这也说明了美国的要素扭曲程度小于中印，这也同本文暗含的假设相同；而随着时间的增长，中国的总TFP收益在变小，而相反印度的总TFP收益在变大，这说明了中国的要素扭曲程度在逐年变小而印度的要素扭曲程度却在逐年变大。

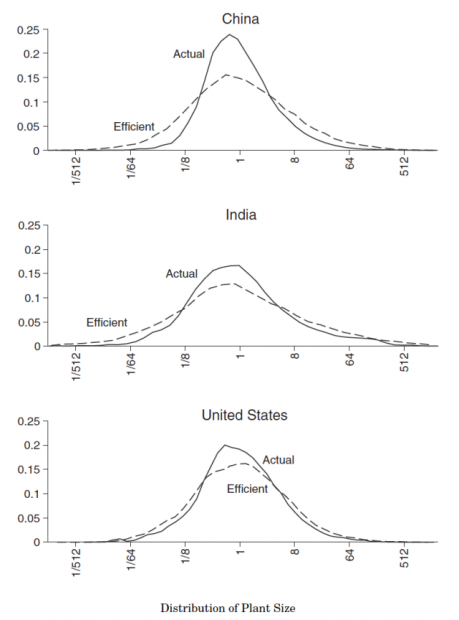
上图显示了中美印三国在要素扭曲为零（均为最后一年）时企业规模分布变化。一般意义上来讲，图中的实线和虚线下覆盖的面积为产品总产出（尽管是下游中间产品），中印两国在消除要素扭曲后产品总产出上升，这说明了消除要素扭曲后对于社会总体福利的改善有着积极作用，而美国的产品总产出没有明显的上升，这可能是由于模型的设定存在一定的问题导致的失真，这也是前文作者将美国定位于“critical benchmark”的原因。

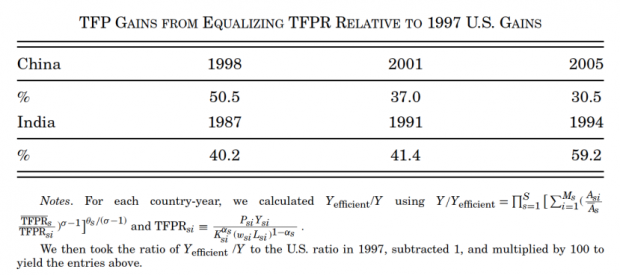
上图显示了本文最为核心的反事实分析的结果，即中印两国将要素扭曲降低至美国水平时的总TFP收益。中国的总TFP将增长30%到50%，而印度的总TFP将增长40%到60%，而同Figure 27的结果类似，随着时间的增长，中国的总TFP收益在变小，而印度的总TFP收益在变大，这再一次印证了了中国的要素扭曲程度在逐年变小而印度的要素扭曲程度在逐年变大。

 

05 结论

 

本文的主要结论有：中美和美印之间确实存在着较大的TFP差异，而要素错配或要素扭曲是造成这一差异的重要原因；当将中印两国的要素扭曲水平设定在美国的低水平时，中国的总TFP将增长30%到50%，而印度的总TFP将增长40%到60%；而随着时间的增长，中国的要素扭曲在逐渐减小，而印度的要素扭曲水平在逐渐变大，在1998-2005的时间跨度内，中国的要素扭曲每年减少2%，而尽管在1991-1994的时间跨度内印度施行了一系列经济改革，但仍旧没有改观。而作者结合敏感性分析指出，本文的结论实在假设模型没有过大的测量误差，没有企业的进入退出策略改变和其他政策扭曲的基础上得出的。

 

Abstract

 

Resource misallocation can lower aggregate total factor productivity (TFP). We use microdata on manufacturing establishments to quantify the potential extent of misallocation in China and India versus the United States. We measure sizable gaps in marginal products of labor and capital across plants within narrowly defined industries in China and India compared with the United States. When capital and labor are hypothetically reallocated to equalize marginal products to the extent observed in the United States, we calculate manufacturing TFP gains of 30%–50% in China and 40%–60% in India.