推文人 | 敖翔

原文信息：Lu F, Anderson M L. Peer effects in microenvironments: The benefits of homogeneous classroom groups[J]. Journal of Labor Economics, 2014, 33(1): 91-122.

 

一、引言

 

这篇论文基于随机实地实验的方法研究了微观环境中的同伴效应。以往关于中小学教育中同伴效应（peer effect）的研究多将同伴定义在教室或学校层面，进而考察学生是否受到班级层面或者学校层面平均水平的影响，但这样可能会忽略更小层面的群体之间的相互影响。陆方文老师和她的合作者在这篇文章中，在中国一所中学里对初一学生开展了一项随机分配座位的实验，研究了在更小的范围中的同伴效应。和欧美中学不同，我们国家中学的学生大部分都是坐在固定教室的固定座位上，不同科目老师轮流在教室上课。在本文的实验中，学生根据身高被分配到不同的block中，然后再在每个block内部随机分配座位，这样block内部的随机分配使得研究更小范围内的同伴效应成为可能。

 

论文研究发现，一个学生周边的其他学生性别会影响这个学生的成绩，但这个影响因性别而异。对于一位女生而言，周边是五位女同学（而非五位男同学）会使得她的考试成绩提高0.2-0.3个标准差，而对于一位男生而言，周边是五位男同学（而非五位女同学）并不会降低他的考试成绩，反而会使他的成绩提高0.1-0.3个标准差。

 

这个研究结果意味着在教室中重新安排学生座位可能可以获得福利的改进，相反论文并没有发现一个学生的学习成绩会被周边同学的基准考试成绩所影响。本文的研究结果适用于同伴效应中诸多模型中的“boutique”模型，强调同质性的同伴群体所产生的收益，并认为合作学习行为是最可能的潜在机制。

 

二、实验设计

 

实验在中国一所普通的公立中学的初一学生中进行。Fig 1清楚的展示了教室的设置，每张课桌坐两位同学，教室分为四列，所以每行四张课桌，课桌之间是过道。根据教室学生数量不同，每个教室有6-8行的课桌，学生在上课和自习时间必须坐在安排好的固定座位上，所以大多数情况下学生只能和邻近的同学交流。由于每列的学生会定期轮换位置，这样使得某一列学生不会一直在教室边上，所以学生与过道另一边的同学形成持续性的同伴关系的机会更少，更多的是和同桌及前后排的同学之间形成稳定的同伴关系。

 

由于在实验中，每列的同学是固定的，本文在每列内部来定义同伴。第一个定义是同桌，第二个定义是“邻近4位同学”,也就是同一列中分别坐在其前后两张课桌上的两位同学。对于坐在第一排和最后一排的同学，他们的“邻近4位同学”就没有四位了。最后一个定义是“邻近5位同学”，也就是同桌加上前后各两位同学。看一个具体例子，如Fig 1所示，在第二行第二列的同学1，他的同桌是同学2，同学3-6是他的“邻近4位同学”，同学2-6是他的“邻近5位同学”。但是对于同学3，没有同学坐在她前面，所以她的“邻近4位同学”只有两人（同学1和2），“邻近5位同学”只有3人（同学1，2，4）。

在2009年秋季入学的第一周，实验人员得到每个教室中学生的姓名、性别和身高信息。基本座位分配机制如下：首先，在每个教室内部将学生按身高由低到高排序，然后前八位学生被分配在block1（对应第1行），接下来16位同学被分配在block2（第2和3行），然后继续16位学生一个block，直到所有学生被分配到对应的block中。身高超过1.69米的同学被分配到单独的一个block当中。最后生成一个随机序列，在每个block内部学生被随机排序并分配到block内的座位上去。这样身高较矮的同学组总是坐在较高同学组的前面，尽管在一个block内部，由于是随机安排的，身高较高的同学可能会坐在较矮同学前面，但是一个block内部学生身高大致接近。在样本中，男女生比为1.27:1,由于7年级时候男女生身高差别不大，实验人员4位男生和4位女生放在第一个block中，在后面的每个block中安排9个男生和7个女生（一个女生对应1.28个男生），直到这样安排不下去为止。不可避免有一些学生因为近视或者家长要求分配到更好的位置，这样的学生大概占了9%，研究人员把他们安排在前排或者中间列，每个block内剩下的其他学生都是随机分配座位的。因此，正常情况下的学生相对于他们的同伴来说是随机的，但是受照顾的学生不是，并且受照顾的更有可能挨着坐。由于这些受照顾的学生不是随机分配座位的，作者在分析结果变量中把他们剔除掉了（尽管包括进来也不会影响结果的稳健性），但是在构造周边的同伴变量（解释变量）时还是用到了他们。此外，在所有回归中，作者也控制了同桌是否是受照顾的学生，以及“邻近4位同学”中受照顾的学生比例，确保性别和基准考试成绩不是受照顾学生的代理变量。对于包括或者排除这些控制变量，结果都是稳健的。研究人员要求班主任老师配合采用随机分配座位的方式，避免在学期内调整座位，学生本人并不知道这个研究实验。但是仍然有可能班主任老师在学期中调整了座位使得一些学生离开了之前分配的座位，所以严格意义上本文估计结果代表的是“intent to treat”的效应。

 

三、数据和实证框架

 

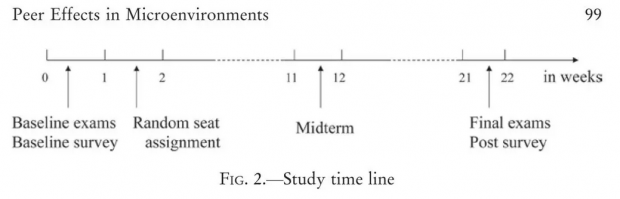
本研究的数据包括对2009年秋季七年级学生的三轮考试成绩和两轮调查。Fig 2展示了学期中按周划分的数据收集时间线。基线考试和基线调查在随机分配座位之前的第一周进行，在第二周进行了随机分配座位，学生被打乱班级顺序分布在10多个教室中进行期中和期末考试，考试时每个学生身边都不是同班的同学。在期末考试结束后学生还留在考试座位上时就马上进行第二轮调查，这样考试结果和调查结果在同伴之间的相关性就不太可能是因为学生之间的交流所导致。在基线考试中，学生参加了语数外三门科目的考试。在期中和期末考试中，学生多参加了政治、历史、地理和生物四门科目的考试。语数外各150分，其他四门各50分。研究中将期中和期末考试的七门课程成绩加总并标准化。在调查中，除了学生的性别，身高和考试成绩外，也调查了学生的家庭背景、兴趣爱好和学生对同伴影响的看法。

如前所述，本文定义了三种类型的同伴效应：同桌、“邻近4位同学”和“邻近5位同学”。对于每种类型的同伴效应，作者构造了两类同伴特征的度量：性别组成（同桌是否是女生，邻近4位同学或者5位同学中女生的比例）和基准考试总成绩。

 

随机实地实验需要对随机分配机制进行验证，这里作者估计了如下方程：

 

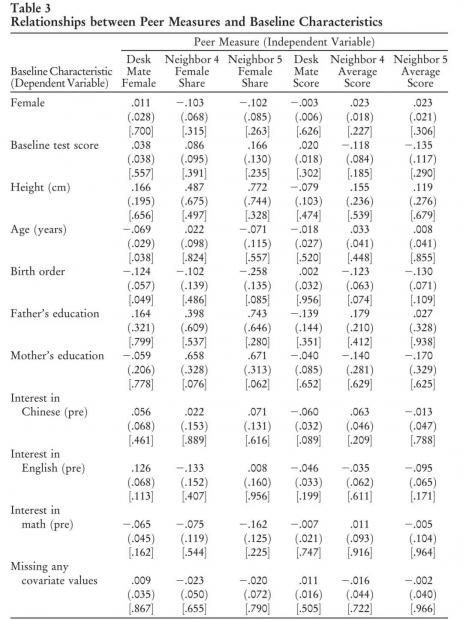
Table 3给出了基准特征对同伴特征两种度量的回归结果，每个cell里面都是一个单独的回归结果。在Table 3的66个回归结果中，只有2个结果（年龄与同桌性别，出生顺序和同桌性别）显著。尽管如此，后面的回归中作者还是控制了基准的特征。

四、结果

 

A.同伴效应对学习成绩的影响

 

 

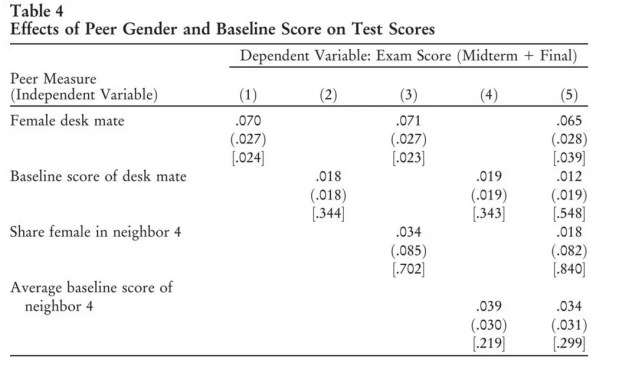
Table 4展示了方程(2)的估计结果。每一列是一个单独的回归。第1列是考试成绩对同桌性别（和其他控制变量）的结果，同桌是女生提高了学生成绩约0.07个标准差。第2列是考试成绩对同桌基准考试成绩的回归，影响不显著。第3列在第一列基础上加入邻近4位同学的女生比例，第4列在第2列基础上加入邻近4位同学的基准考试成绩。因为在随机分配座位机制下同桌和邻近4位同学应该是不相关的，加入这些并没有影响同桌性别或者同桌基准成绩的系数。邻近4位同学的性别和基准考试成绩系数虽然为正但都不显著。第5列的回归同时包括了前4列所有的同伴效应，只有同桌性别是统计显著，系数大小没有受到太大影响。因此，我们可以排除坐在基线考试分数高同学旁边会有很大的影响。

B.异质性处理效应

 

异质性处理效应具有政策意义，提供了通过安排学生座位提高总体成绩的可能性。Table 5的panel A第1和2列分别展示了对女生和男生估计得到的同伴性别组成和基准考试成绩的影响。女性同桌变量系数虽然为正，但是对于男生和女生都不显著。对于女生而言，邻近4位同学中女生比例的系数为正并且显著，对于男生而言，该系数为负且不显著。因此，我们可以排除身边坐4个女生会对男生成绩产生很大的积极影响。同桌和邻近4位同学的基准考试成绩对于男生和女生的影响都很小且不显著。第3列报告了女生和男生估计系数之差。邻近4位同学中女生比例对女生和男生的影响差别很大且统计显著，其他差异不显著。

 

Table 5的Panel B用邻近5位同学替代同桌和邻近4位同学来评估两者的综合影响。第1列结果证明女同学对邻近的女生有积极且显著的影响。这意味着将一个女生从邻近都是男生的环境换到邻近都是女生的座位会使得她的成绩提高接近0.2个标准差。但是第2列结果表明女同学对邻近的男生成绩没有显著影响，且系数为负。邻近5位同学的平均基准考试成绩对男生或者女生的考试成绩都没有显著影响。第3列中邻近5位同学中女生比例对女生和男生的影响之差为0.33个标准差。

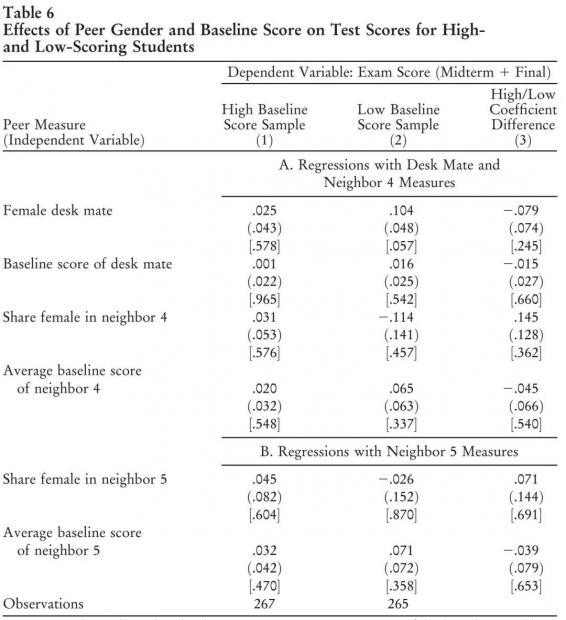
Table 6展示了分别对基准考试成绩高和低的学生分别估计的同伴效应。Panel A的第1列展示的结果来自基准考试成绩在中位数之上的学生样本。这个样本的结果中，所有度量同伴效应的变量的系数都接近于0并且不显著。第2列的样本只包括基准考试成绩在中位数之下的学生样本。这个样本中，女性同桌的影响为正并且边际上显著，其他同伴效应则不显著。第3列报考了两组样本的系数之差，统计上都不显著。Panel B分别对基准成绩高和低的同学评估了邻近5位同学的总体影响。在两个样本中都没有发现相邻同学性别或者基准成绩的显著影响。第3列报告了两组样本的系数差异，结果很小且不显著。这意味着，与性别不同，根据基准考试成绩来将学生分别排座位几乎没有任何更多好处。成绩好的学生对其他成绩好的学生的帮助看起来并不会比她们对成绩差一些的同学帮助更大。

作者另外做了两组稳健性检验。一是，由于对于第一排和最后一排的同学而言，“邻近4位同学”和“邻近5位同学”两类同伴中包含的同学人数要更少，作者对把这不包括这两组同学的样本做了稳健性检验，结果类似。最后，作者分别估计了“前排”（正坐在前面课桌的两位同学）和“后排”（正坐在后面课桌的两位同学）同伴特征的影响，结果发现女孩特别受益于其他女生坐在她前面，而男生特别受益于其他男生坐在他后面。

 

五、讨论

 

上面的实验结果证明性别相同的环境可以提高学习成绩，当坐在其他女同学附近时候，女生成绩会更好，而男生坐在其他男同学附近时成绩也会更好。关于同伴效应研究有很多理论模型，作者一一讨论了同伴效应中主要的模型和她们实验结果的关系，认为the “boutique” model是最符合她们研究结果的模型。The “boutique” model假定当学生周围的同伴和他相似时候他会表现的更好，这可能是因为相似性使得学生更容易互相帮助，或者老师可以为每个群体的学生量身定制课程学习内容。

 

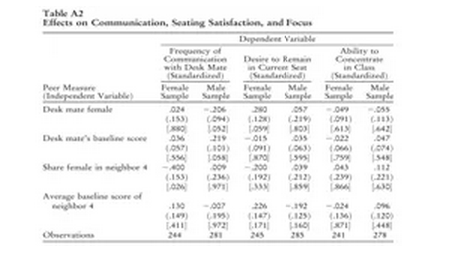
作者最后讨论了论文中同伴效应的三个潜在机制，一是教师有机会针对特定的学生类型（本文中男生或女生）定制课程内容，二是在同质的群体中捣乱行为的减少，三是协作学习或者积极互动行为的增加。但是由于本文研究的是学生座位周边的同伴效应，所以第一个机制基本可以排除，作者也没有找到第二个机制中捣乱行为减少的证据，认为相同性别同学之间的合作学习行为是本文研究最可信的潜在机制。在最后一次调查中，作者问了关于受调查学生和其同桌关系的几个问题，包括和同桌交流的频率，多么希望继续坐在现在的座位上，上课注意力集中程度等，然后用这几个变量分别对同桌和邻近4位同学以及学业背景进行了回归，结果见Table A2。第1列结果表明，如果将一个女生从前后四个同学都是男生的座位换到前后都是女生的座位，会降低她和同桌交流的频率约0.4个标准差。这可能是因为如果一个女生更加频繁的和前后4个同学交流，会挤占她和同桌的交流。第二，男生和女同桌交流的频率比和男同桌要低0.21个标准差，这个结果和性别同质促进交流是一致的，尽管没有解释为什么男同学没有从男同桌上获益。第三，当同桌为女生时，女同学表达了更强烈的想要留在现在座位上的愿望，这表明女生更喜欢坐在其他女生边上。但是邻近4位同学的女生比例对女同学的座位满意度没有显著影响，所以证据也不一致。最后，当同桌是女生或者身边是女生时，无论是女同学还是女同学都没有表现出能更好的集中精力，这进一步表明捣乱行为的减少不是相关机制。总体而言，调查结果提供了一些证据支持性别同质群体通过合作性的学习行为提高了学生成绩的假设。

合作学习行为也为前文中同桌和邻近4位同学影响的潜在差异提供了一个可能解释。之前的结果表明女生受益于邻近4位女同学，男生受益于邻近4位男同学，但是两者都没有因为同性别的同桌而受益。与同桌的交流难以避免，但是和邻近4位同学的交流是自愿的从而可能更依赖于同伴关系的亲疏。如果性别相同的学生更有可能互相交流，那么我们可以认为有相同性别的邻近4位同学会比有相同性别的同桌带来更大的收益。

 

六、结论

 

与以往基于班级或者学校的同伴效应研究不同，这篇论文利用在中国一所中学里面随机分配座位的实验，首次识别了教室内部更小范围内的同伴效应，这也是本文最大的亮点。研究结果表明，尽管同桌是女同学对于男生和女生可能都有益，但是周边有更多女同学时对女生有显著的积极影响，但是对男生有潜在的负面影响。同桌和邻近4位同学的同伴效应之所以存在差异的可能原因是在于和两者的互动不同：与同桌的互动更容易并且在某种程度上不可避免，但是与前后同学的互动却是自愿的，最合理解释的机制在于相同性别的学生之间合作学习行为的可能性更大。最后，随机实地实验研究往往需要讨论一下结论的外部有效性，作者通过对比研究学校所在的城镇和全国范围内城镇、学校所在地区（包括城乡）和全国地区（包括城乡）的相关特征，发现主要差异在于城乡之间，并且研究对象主要是在青春期的孩子（10-14岁），因此本文结论不一定能推广到农村地区或者年龄更小的孩子群体身上。

 

最后本文的政策含义在于，在中国当前中学教育背景下，通过一种低成本的改进教室中座位分配的方法，可能会带来学生考试成绩的提高，并指出了可以在更小范围内的微观环境中研究同伴效应的价值。

 

Abstract

 

Many believe that classroom interactions play an important role in students’ academic achievement, but there is little evidence on peer effects within subclassroom groups. We exploit random seat assignment in a Chinese middle school to estimate how the gender of neighboring students affects a student’s academic achievement. We find that being surrounded by five females rather than five males increases a female’s test scores by 0.2–0.3 standard deviations but has no significant effects on a male’s test scores. These results suggest a low-cost way to potentially improve performance within the world’s largest school system.