推文人 | 范洋
原文信息:Varian, Hal R. “Big Data: New Tricks for Econometrics.” Journal of Economic Perspectives, vol. 28, no. 2, 2014, pp. 3–28.
推文作者:范洋,博士,毕业于中科院数学与系统科学研究院,现供职于国家信息中心经济预测部。
写的微观经济学教材风靡全世界的范里安范老师被Google挖去了山景城做首席经济学家,写了一篇给经济学家鼓吹(划掉)介绍大数据的文章,发在JEP2014。
大数据条件下,一般用来训练预测模型的样本量都是非常大的。这容易使得模型过于复杂,产生过拟合问题,模型的样本内预测效果很好,但缺乏样本外预测能力。因此,大样本条件下最值得关注的问题,不是如何拟合模型,而是如何解决模型的过拟合问题。
本文介绍了分类和回归树(Classification and regression tree, CART)。并使用R包rpart给了一个简单的应用:预测Titanic号上乘客的生存概率。
树可以预测一些不太线性的变量。此方法特别适用于概率分布不太连续的问题,因为这种情况使用连续模型(logit或probit)预测效果不是很好。
如果说,最小二乘的实质是想要在一个向量空间中寻找到一个与目标向量距离最小的向量,它与目标向量之间的距离是垂直于这个向量空间的,求最小二乘解就是找到这样的线性组合。作为对比来看,树回归的实质就是,用各种属性把样本的分布形态展开到空间中,这些属性可以是任意关系,它不要求空间的线性性。确定属性实际上就是确定回归里面的解释变量。我们要尽量保证用来展开的这个属性是解释性好的,也就是样本在这个属性上展开的概率分布比较有特点,或者更容易刻画。
“大数据”时代,树回归的流行得益于树回归对数据量很大的样本有更好的效果。“logistic regression is better for smaller data sets and tree induction for larger data sets.”(Perlich, Provost, and Simonoff (2003))当然,样本量大很自然地就会引发过拟合问题,树的过拟合问题也需要特别引起关注。这就需要降低树模型的复杂度,给树剪枝。
一种方法是使用下文要讲到的k-fold交叉验证(一般选k=10)。第二种方法,直接使用条件推断树(conditional inference tree,简称CTree),使用一系列假设检验来选择树的结构。第三种方法是在样本中加入一些随机性,方法包括boostrap,bagging,和boosting。bagging主要用于树等非线性模型(Friedman and Hall,2007)。 boosting能显着提高估计量的预测性能,可用于任何种类的分类或回归模型,包括logit,probit,树等。也可以将这些技术结合起来,创建一个“森林”,通常可以显着改进单树方法。
2)在树的每个节点上,随机选择一个样本作出下一个决定。 不要剪枝。4)为了确定一个新样本的预测值(或分类结果),分别使用每个树回归模型,并使用出现次数最多的结果。
对于高度非线性的数据样本来说,这种方法的预测效果非常好。Howard and Bowels(2012) 认为“ensembles of decision trees (often known as ‘Random Forests’) have been the most successful general-purpose algorithm in modern times.”。
1.3 使用k-fold交叉验证(k-fold cross-validation)选择合适的模型复杂度
k-fold交叉验证是将训练集的1/k作为测试集,每个模型训练k次,测试k次,错误率为k次样本外误差的平均,最终选择平均样本外误差最小的模型。流程如下:
3)使用训练出来的模型得到样本外预测值,与被留下的子集比较得出1个样本外预测误差4)对其余k-1个子集,使用相同的方法再得出k-1个样本外预测误差。
对于这个模型来说,其样本外预测误差就是k个样本外预测误差的平均值。
2.1 引入惩罚函数:弹性网回归(elastic net regression)
考虑线性回归的变量选择问题。传统上,变量选择的方法包括逐步回归(stepwise regression),主成分分析(principal component analysis),偏最小二乘法(partial least squares),以及基于赤池信息准则(AIC)和贝叶斯信息准则(BIC)的复杂性度量等。 对于数据量很大的的拟合工作,变量选择的核心关切就成了避免过拟合。本文介绍了Lasso(least absolute shrinkage and selection operator) 及其变体:弹性网回归(elastic net regression):
考虑一个以[b_1,b_2,...,b_n]为系数的线性回归模型,在筛选哪些变量应该进入最终的方程时,我们通过最小化一个包含两部分的函数来实现。这个目标函数的第一部分是传统最小二乘的估计条件,即误差平方和;另一部分是一个如下形式的惩罚函数:
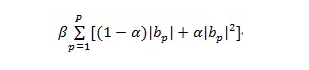
当β取0时,惩罚函数失效,就是普通的最小二乘回归;当α取1时,惩罚函数中只剩下二次项,模型就成为一个岭回归(ridge regression)模型;当α取0时,便是Lasso(least absolute shrinkage and selection operator)。
上述方法可以保证模型中某些最小二乘回归系数收敛于0,这样就实现了变量选择。
2.2 Spike-and-Slab regression
这种方法本质上是一种贝叶斯方法。给定每个系数出现概率的先验概率向量(spike,某个系数不为零的先验概率);根据系数在回归方程中的情况,指定某变量回归系数的先验分布(slab,先验地描述系数可能的取值)。使用MCMC方法求后验信息,尤其是系数出现频率的后验概率。
时间序列模型中的变量选择问题除了过拟合,还有序列相关。在日常使用Google Trends数据进行时间序列分析时,很难确定哪些序列有较好的预测效果。尽管Google Trends将数据序列集进行了初步分类,但仍然收效不大,如何解决过拟合与序列相关是核心的问题。本文简要介绍了一种估计方法用来解决这个问题,BSTS(Bayesian Structural Time Series)。考虑一个有常数项、线性时间趋势和回归项的经典时间序列模型:

另外,合适的话也可添加季节性状态变量。待估参数为β和e_it的方差,可使用卡尔曼滤波来估计。
与计量里对因果推断的强调有所区别的是,机器学习模型一般是用来预测的。但是,尽管机器学习模型无法直接识别变量之间的因果关系,我们仍然可以通过机器学习模型的预测结果来估计一项政策或一个事件的影响,这一思路可以类比社会实验,有“observed difference in outcome = average treatment effect on the treated + selection bias”(Angrist and Pischke, 2009)。当然如果我们有一个真正的可控制变量的对照实验,那么选择偏误就可以完全消除。
本文给出了一个例子,估计广告投放对网站访问量的因果影响(Lewis and Lao, 2013)。具体流程是,使用前面提到的BSTS(Bayesian Structural Time Series)方法,用历史数据来估计如果没有投放广告(假设其他因素例如季节性等均不发生变化)时网站访问量。值得一提的是,由于影响预测结果的因素很多,这里要考虑使用前文中提到的变量选择技术。将预测结果与实际投放广告之后的网站访问量作对比,可看到广告投放对网站访问量的明显改善。
这一流程并没有使用通常意义上的对照实验,但一个好的预测模型,在进行因果推断的时候甚至比对照实验效果更好。因为对照实验无法灵活地更改实验设计时确定的控制变量,而预测模型则可以方便地做到这一点,使得“实验”结果更为可靠。
我们可以从机器学习的经验里得到一个很重要的思想:对许多小模型进行平均可以比选择单个模型更好地进行样本外预测。其实在很早之前,人们就已经认识到宏观经济预测中,将预测模型进行平均之后的预测效果也优于单个模型,但不知何故,除了贝叶斯模型领域,这种想法在传统文献中很少使用。
现在的应用计量文献中,许多论文都将不同的模型呈现在一张表格中,用来说明某一重要参数的估计是鲁棒的,对使用什么样的模型不是很敏感。
那么考虑一下,如果我们使用这些表格来说明:随着使用不同的模型,估计的参数是如何变化的。目前论文中,作者倾向于只研究一些有代表性的规范,但没说为什么如果数据可用,他们不能再检查更多的情形。
在这个“大数据”时期,很大的样本数据量极大地减轻了样本不确定性,而模型不确定性却可能相当之大。传统的计量经济学将研究重点放在样本不确定性,而模型不确定性才可能是大样本条件下更应该关注的问题,解决这个问题的一种方法是明确地研究参数估计如何随控制变量和工具变量的选择而变化。
“大数据”时代,样本量的丰富极大地影响着经济研究。
首先,当模型不再受制于样本不够大的约束,我们可以考虑尽可能多的影响因素。新的问题就此产生。树回归的重要考虑,以及多种变量选择方法的本质,都是要回答这么一个问题:如何从这些影响因素中提取出解释力最强的属性。
其次,样本量的丰富使得“过拟合”而非“欠拟合”成为估计的核心关切,提高模型的泛化能力基本上等同于去惩罚模型的过拟合。
第三,传统计量重视样本不确定性,而在样本量很大的情况下,样本不确定性大大减小,而模型的不确定性则更为重要。
最后,注意到在文章的开篇,范里安在介绍“大数据”为什么发展得这么快时,说:“The ability to rent rather than buy data storage and processing has turned what was previously a fixed cost of computing into a variable cost and has lowered the barriers to entry for working with big data.”显然,对于固定成本、可变量成本和竞争壁垒的分析是他作为一个严谨经济学家的根本所在。
Computers are now involved in many economic transactions and can capture data associated with these transactions, which can then be manipulated and analyzed. Conventional statistical and econometric techniques such as regression often work well, but there are issues unique to big datasets that may require different tools. First, the sheer size of the data involved may require more powerful data manipulation tools. Second, we may have more potential predictors than appropriate for estimation, so we need to do some kind of variable selection. Third, large datasets may allow for more flexible relationships than simple linear models. Machine learning techniques such as decision trees, support vector machines, neural nets, deep learning, and so on may allow for more effective ways to model complex relationships. In this essay, I will describe a few of these tools for manipulating and analyzing big data. I believe that these methods have a lot to offer and should be more widely known and used by economists.





 京公网安备 11010502034662号
京公网安备 11010502034662号 