图片来源：百度图片

原文信息：SCHWERT, M. (2017), Municipal Bond Liquidity and Default Risk. The Journal of Finance, 72: 1683-1722.

原文链接：

https://onlinelibrary.wiley.com/doi/full/10.1111/jofi.12511

01

主要内容

本文探讨了美国市政债券的定价问题。关于市政债券定价的文献主要关注税收减免和流动性不足两方面——免税吸引大量散户交易，高交易成本导致流动性不足，但是鲜少关注债券的违约风险对定价的影响。本文使用1998-2015年美国市政债券数据，通过三种不同的、互补的方法将市政债券价差分解为违约风险和流动性风险两部分，第一种方法使用交易数据估计流动性风险价差，第二种方法使用CDS数据估计违约风险价差，第三种方法通过再融资这一准自然实验估计违约风险价差的下限。结果表明，违约风险贡献了市政债券价差（税收调整后）的74%-84%，由于市政债券违约罕见，这表明违约风险有较高溢价。

02 

债券收益率分解

价差（市政债券与无风险债券收益率之差）由两部分组成：①违约风险价差：包括违约可能、违约预期损失、信用风险的市场价格等；②流动性风险价差：由于市政债券是场外交易，主要由散户投资者持有，因此会产生大量交易成本。下面用公式刻画分解过程。

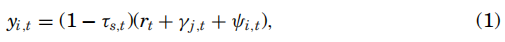
  为第 期市政债券 的收益率。 为第 期州 内投资者的边际税率, 假定州内发 行的所有债券边际税率相同。胃于数据限制, 无法估计同时考虑违约和流动性情况下的边际 税率, 根据 Longstaff (2011) 和 Kueng (2015) 估计的 “边际税率接近但略低于法定最高税 率” 这一结果, 本文取各州所得税的法定最高税率。 为第 期的基准利率, 根据 Feldhutter （2008）, 美国国债收益率可能受到一些特殊利益的影响从而低于无风险利率, 因此本文取 溢价和掉期利率作为基准无风险利率。 为第 期发行人 的违约风险, 由于市政债券 主要还款来源为税收，因此本文假定同一发行人发行的所有债权违约概率和预期损失相同。 为第 期市政债券 的流动性风险价差, 反映预期交易成本以及交易成本增加的风险。
 

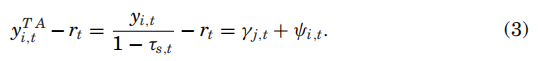
（1）式变形得到（3）式，税收调整后价差可以分解为违约风险价差和流动性风险价差两部分。本文分别使用三种分解方式进行计算：①基于交易数据估计流动性风险价差，进而作差估计违约风险价差；②基于CDS数据估计违约风险价差，进而作差估计流动性风险价差；③通过准自然实验估计违约风险价差和流动性风险价差。

1.基于交易数据估计流动性风险价差

 沿用Dick-Nielsen et al.（2012）的分解方法，本部分使用交易数据直接估计流动性风险价差，那么剩余部分就是违约风险对应的价差。

被解释变量为税收调整后价差。关键自变量为流动性变量，由Amihud（2002）、Feldhutter（2012）、Roll（1984）提出的几个流动性度量指标近似加权平均得到：

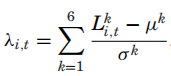
其中,  为流动性度量指标的原值, 包括 Amihud 测度等六个变量;  为均值,  为标准差。类似的, 本文构造了交易活动度量指标 , 由交易间隔、零交易、负交易等变量加权平均获得;   为换手率。之所以采取这种方式构建自变量, 是为了降低维度。此外, 回归中加入债券评级变量以减小遗漏变量偏误。
 

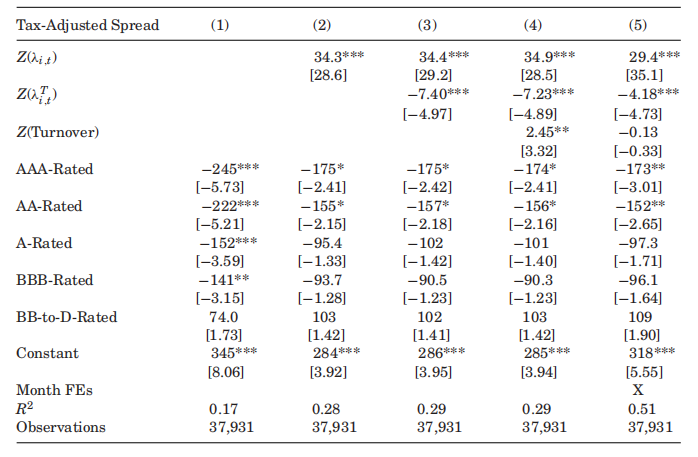
根据回归结果,  系数显著为正，意味着交易成本越高, 价差越大, 交易成本每增加 1 个标准差, 税收调整后价差增加  个标准差。  系数显著为负意味着交易强度越低, 价 差越小, 这与 Amihud（1986）的结论一致, 流动性折价随着交易强度增加而增加。

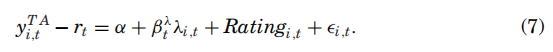
为估计流动性风险价差, 本文沿用 Dick-Nielsen et al. (2012) 的分解方法将税收调整后价差直接回归在流动性度量指标  上。并根据（8）式计算流动性风险价差 , 其中  为第一百分位数。根据 (3) 时可以求出违约风险价差 。

该方法可能存在一些潜在问题：第一，如果流动性和违约风险是正相关的，那么可能会低估违约风险价差；同样，如果出于某些因素流动性被低估，那么违约风险价差将被高估。第二，将市政债券在第一百分位处的流动性作为基准可能并不准确。因此，本文使用两种替代方法分解价差。

2.基于CDS数据估计违约风险价差

沿用Longstaff et al.（2005）的分解方法，本部分假定CDS溢价代表了违约风险价差，通过比较税收调整后价差和CDS溢价，将差异定义为非违约风险部分，比如搜索等交易成本。该方法的好处是，CDS是一种直接的信用风险衡量标准，受市场摩擦的影响较小。该方法的弊端是，CDS发行方只是债券发行方的一个子集，并且2008年之前无交易数据。

3.通过准自然实验估计

发行方可以通过再融资预先规避违约风险，再融资是指在赎回日之前预先发新债还旧债，将收益持有为信托基金，为剩余付款提供资金。假定再融资前后流动性风险价差不变，那么被解释变量税收调整后价差的变动便是违约风险部分带来的。Ang et al.（2014）研究发现再融资之后流动性恶化，因此税收调整后价差的变动是违约风险价差的下限。

本文用再融资时间前后一年的数据进行回归。关键自变量为再融资事件的 0-1 变量, 控 制信用评级、时间、规模, 以及债券固定效应和月固定效应。回归系数  是债券再融资前后 平均价差 (税收调整后) 的变化, 也是违约风险价差的下限。

03 

实证结果及其比较

1.基于交易数据估计流动性风险价差

1998-2015年，债券经税收调整后的价差为131bps，分解为违约风险价差101bps和流动性风险价差30bps。因此，违约风险贡献74%，流动性风险贡献26%。下图绘制了平均税收调整后价差、违约风险价差和流动性风险价差的时间序列。整体来看，税收调整后价差在1998-2003年保持稳定，2003-2005年大幅下降，2008年初急剧上升，增加了近两倍。金融危机后，税收调整后价差逐步下降至2014年的最低水平，波动性依旧很高。违约风险价差在整体价差中占比一直较高。

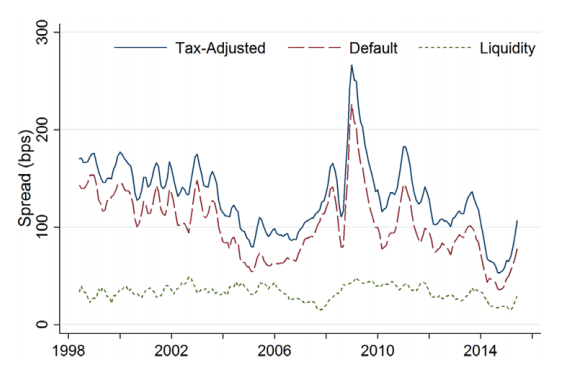
2.基于CDS数据估计违约风险价差

基于CDS分解的替代方法直接衡量税收调整后价差的违约部分。下表比较了17个独立州分别基于交易数据和CDS数据的方法，结果显示，在基于交易数据的方法中，违约风险对税收调整后价差的贡献在60%-86%之间；在基于CDS数据的方法中，其范围为62%-104%。两种互补的方法结果较为一致，这增强了我们对结论的信心。

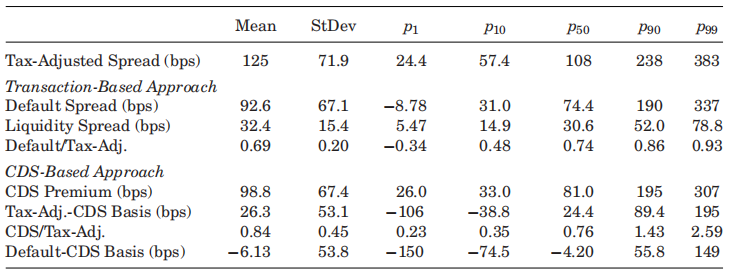
值得注意的是，基于交易数据分解的方法有两个潜在缺点：第一，税收调整后价差可能由于测量误差或不受控制的信贷风险影响产生偏差；第二，衡量流动性风险价差选取的基准是流动性非常强的市政债券，这一基准可能明显低于基准掉期利率。下图绘制了基于交易数据和基于CDS数据分解得到的流动性风险价差，在金融危机期间，基于CDS数据分解得到的流动性价差比基于交易数据分解高出50-100bps，这证实了上述担忧。

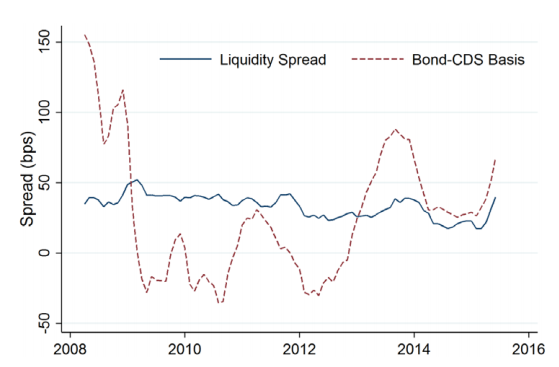
3.通过准自然实验估计

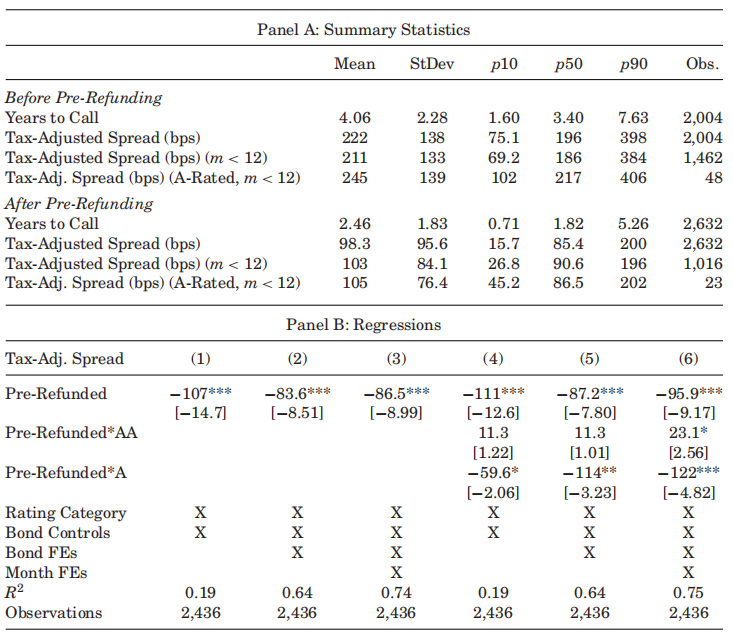
下表报告了通过再融资时间这一准自然实验衡量违约风险价差下限的结果。Panel A为描述性统计，再融资后的交易平均发生在距离第一个赎回日期的2.46年，债券经税收调整后的价差在再融资前一年为211bps，在再融资后一年为103bps，这与再融资降低违约风险的预期相一致。Panel B报告了回归结果，再融资之后税收调整后价差降低了86.5bps（41%），对A级债券来说再融资使得税收调整后价差降低了218bps（89%）。假定市场流动性利差不变，那么在再融资发生之前，违约风险价差至少占税收调整后价差的41%。

4.解释违约风险价差的水平

上述三种方法都表明，违约风险贡献了税收调整后价差的大部分。但是，从历史数据来看，市政债券违约事件极其罕见：1970-2014年，美国所有评级市政债券的五年累计违约率为0.08%。结合上述两点，本文认为市政债券市场的违约风险溢价很高，并对违约风险溢价进行了一定的量化，囿于篇幅限制，不再一一展示。

04 

总结

本文使用三种方法对市政债券价差（剔除税收因素）进行分解，结果表明违约风险在市政债券价差中起主要作用，而流动性风险起次要作用。结合市政债券违约率较低这一现实情况，本文认为市政债券违约风险溢价比企业债券高很多。在政策启示上，本文认为交易成本和流动性风险对于降低政府融资成本而言作用不大，应该考虑如何减小风险溢价。市政债券风险溢价的一个潜在来源是免税：第一，免税政策对边际税率较低的投资者而言没有太大影响；第二，大多数州只免除了地方债券的州所得税，使得各州市场细分，不完善的风险分担可能会带来风险溢价。

05 

拓展

在防范化解地方政府债务风险这一问题上，我们关注的债务风险往往是地方政府无法清偿到期债务的偿债风险。除负债率、债务率等指标衡量债务风险外，本文提供了新的视角：通过测算地方政府债券和城投债的风险溢价，从市场的角度测度地方政府债务的违约风险。

本文提供了一个较为丰富全面的收益率价差分解的方法。王永钦等（2016）借鉴本文思路，从交易城投债的金融市场角度将收益率价差分解为流动性风险价差和违约风险价差两部分，分解思路为：首先基于交易数据估计流动性风险价差，然后从总的城投债收益率价差中剔除流动性风险价差，得到违约价差部分。之后利用货币政策变动、汇率变动和金融危机等对于地方政府而言外生的冲击通过DID的方法进一步识别中国地方政府隐性债务的违约风险是否被正确定价。结果发现，地方政府的违约风险没有在收益率价差中得到反映，但是中国整体违约风险被有效定价，这表明中国地方政府债务存在软预算约束问题。

Abstract 

This paper examines the pricing of municipal bonds. I use three distinct, complementary approaches to decompose municipal bond spreads into default and liquidity components, and find that default risk accounts for 74% to 84% of the average spread after adjusting for tax-exempt status. The first approach estimates the liquidity component using transaction data, the second measures the default component with credit default swap data, and the third is a quasi-natural experiment that estimates changes in default risk around pre-refunding events. The price of default risk is high given the rare incidence of municipal default and implies a high risk premium.

声明：推文仅代表文章原作者观点，以及推文作者的评论观点，并不代表香樟经济学术圈公众号平台的观点。