推文人 | 裴相烨 

 

原文信息：Combes, P. P. , Duranton, G. , Gobillon, L. , & Roux, Sébastien. (2010). Estimating agglomeration economies with history, geology, and worker effects. Nber Chapters.

 

生产率会随密度增加吗？本文使用法国的工资和全要素生产率数据重新审视这个问题。一是用工具变量方法剔除劳动力数量对估计结果的影响，并在历史工具变量的基础上增加了地质工具变量。二是用劳动力固定效应方法剔除劳动力质量对估计结果的影响。研究发现，劳动力数量会造成估计结果的偏误，两组工具变量都证实了这一点。此外，劳动力质量对估计结果偏误的影响程度更大。本文的思路简洁明了，主要分为三个部分，第一：介绍了估计模型并分析了存在的内生性问题；第二：介绍了使用的数据以及工具变量；第三：进行了回归分析并对比相关结果。

 

01 引言

 

在较大的城市或者人口密集的地区，生产率和工资往往更高。一般来讲，生产力相对于就业密度的弹性通常在0.04-0.10之间，本文根据法国的数据证明了这一结论。图1a显示了306个法国就业地区1976年至1996年期间平均工资的对数与就业密度的关系，测得工资密度弹性为0.05；图1b使用306个就业地区1994年至2002年期间TFP的对数进行了类似的研究，测得TFP密度弹性为0.04。

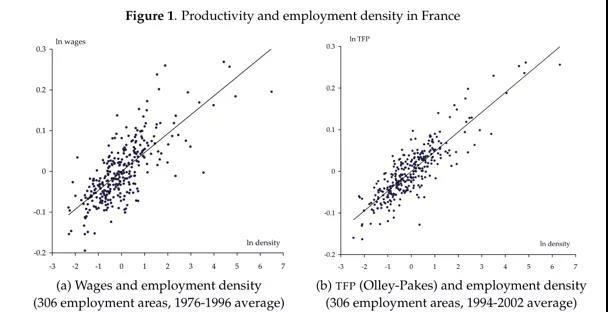
由图1可推断出两个基本的识别问题。第一，密度和生产率(工资或全要素生产率)是互为因果的，也就是说生产率更高的地方往往会吸引更多的劳动力，从而提高密度，也可以说缺少与密度和生产率相关的变量产生了遗漏变量问题，本文称之为劳动力数量带来的内生性问题。自Ciccone and Hall（1996）文章发表以来，解决这个问题的一般方法是使用工具变量。第二，生产率更高的劳动力类分到密度更高的地区，出现这种情况可能源于密度越高的地区基础设施越好，或者密度高带来的生产率优势对熟练劳动力的影响更大等，本文称之为劳动力质量带来的内生性问题。自Glaeser and Maré (2001)文章发表以来，解决这个问题的一般方法是使用数据的纵向维度。

 

此外，密度可能会以多种方式直接或间接影响生产率(Duranton and Puga, 2004)。例如，带来更高效率的共享（sharing），更高质量的匹配（matching），或者促进对新技术的学习（learning），但本文并不探究密度对生产率影响的具体机制，而只估计密度对工资的总净效应。一是用工具变量方法剔除劳动力数量对估计结果的影响，并在标准历史工具变量的基础上增加了地质工具变量。二是用劳动力固定效应方法来剔除劳动力质量对估计结果的影响，利用工资数据的纵向维度来进行回归，将地区效应与个体效应分开分析。

 

本文主要结果如下：平均工资对密度的弹性略低于0.05，仅剔除劳动力数量带来的影响，这一估计降低到0.04左右，历史和地质工具变量得出大致相同的结果；仅剔除劳动力质量带来的影响，弹性估计值是0.033；同时剔除劳动力数量和质量带来的影响，密度弹性降低为0.027；当考虑市场潜能带来的影响时，工资对密度的弹性估计结果为0.02。此外，使用TFP衡量生产率时，上述结论仍然成立。因此，本文认为在剔除了劳动力数量和质量带来的影响后，仍然存在较小的集聚效应；从量化结果上看，相比于劳动力无差别的集聚，劳动力的类分带来的影响更大；在生产率测度时，相比于TFP等其他指标，工资是最优的生产率测度变量，因为工资数据中包含了不可观测的劳动力能力特征。

 

02 估计集聚效应存在的识别问题

 

本文建立了理论框架，帮助我们理解地区特征与工资或生产率之间的关系。概括来说，设立了一个C-D函数，假设所有企业面临相同的利率、全要素生产率由一系列的本地特征变量决定，进而分别得出了工资、产出与本地特征的回归方程，并据此分析存在的内生性问题。

 

具体而言，模型的基本设定为规模报酬不变的竞争性厂商i，其产出取决于资本、劳动力、全要素生产率，则其生产函数为：

第一个问题是劳动力数量带来的内生性问题。一是遗漏变量问题，即地区特征变量的选择有很多，但回归时只选择了一部分变量，其余变量在误差项里面，因此，是存在相关性的。二是反向因果问题，即生产率更高的地方往往会吸引更多的劳动力，从而提高密度。因此，在人口空间分配缺乏大规模随机试验的情况下，几乎任何描述一个地区就业和生产结构的变量都可能被怀疑是内生的。第三，资本价格可能是变化的。若为物质资本，其价格在地区间不存在差异，那么与价格相关的变量就变成常数项。然而，若为土地资本，则其价格在地区间是存在差异的，会对估计结果造成影响。Roback (1982)提出，更好的消费设施(可能与生产完全无关)将吸引更多的人口，进而提高土地价格。这说明非生产变量影响了土地价格，进而影响了生产函数，可以尝试控制直接影响消费者效用的地区特征变量来剔除这一影响。然而，控制变量是有限的，本文并未使用较多控制变量，因为很多变量可能与工资存在反向因果的问题，最终本文采用寻找工具变量的方法来解决这个问题。

 

第二个问题是劳动力质量带来的内生性问题。首先，地区平均工资不能体现劳动力特征，所以不同地区之间是无法比较的。其次，模型中探讨的是单位劳动效率的工资率，而个体劳动者的工资数据是日收入，即单位劳动效率的工资率乘以劳动效率。因此，需要在回归中剔除个人技能的影响，本文使用数据的纵向维度来解决这个问题。

 

03 工具变量

 

本文选取了历史工具变量与地质工具变量。概括而言，历史工具变量与核心解释变量的相关性在于人口空间分布具有一定的持久性，而外生性在于对一个地区来说，过去和现在高生产率的驱动因素是不同的。就法国地区而言，控制了环境舒适度后，过去人口集聚的驱动因素与现在生产率的决定因素无关，即1831年和20世纪末的经济区别较大，包括经济结构、生产技术、运输成本、政治环境等诸多方面的不同，例如，1831年法国刚刚开始工业化进程，然而现在正在去工业化，农业、制造业和许多服务业的生产技术与150多年前有了根本的不同，而且随着欧洲一体化的发展，贸易也越来越容易，此外，自1831年以来，法国由国王、皇帝以及来自五个不同共和国的总统和总理统治，政治环境改变较大，充分说明了过去人口分布的决定因素并不是目前影响生产率的主要因素。

 

地质工具变量与核心解释变量的相关性在于肥沃的土壤能够吸引更多的人口，而且土壤之间的性质存在差异，有些土壤比其他土壤更稳定，可以支持密度更高的经济活动，而外生性在于土壤不以其他方式影响生产率。具体而言，土壤特征大多数是由自然决定的，而不是人类活动的结果，如优势母质、土壤矿物质是几百万年前确定的。此外，当农业占就业人口不到5%的情况下，土壤质量与经济发展（制造业/服务业）是不相关的，从而确保外生性。但也存在一些质疑，如土壤的岩石深度或者含碳量可能与人类活动有关、某些土壤特性难以衡量等问题，但本文使用了丰富的土壤特征变量，在不同的回归中利用不同的土壤特征组合作为工具变量，并通过过度识别检验确保一些土壤特征的外生性。

 

历史工具变量来自早期法国人口普查数据，分别为1831年与1881年人口密度，为了最小化弱工具变量带来的问题，删掉人口不超过5000个的35个就业地区。地质工具变量来自ESDB，选取了12个变量，具体包括土壤性质、特征以及地形变化等，并以就业区为基本空间单元对栅格数据进行了转换和加总。两种工具变量均通过了相关性检验，并满足外生性。

 

04 工资与TFP的来源与测算方法

 

工资数据来源于《社会数据年鉴》(DADS)以及法国统计局(INSEE)的年度社会数据库的数据，具体包括劳动力的性别、年龄、二位数职业代码、工作天数/年、收入以及雇主的位置、三位数部门代码。在处理过程中，选取偶数年10月出生的制造业与服务业行业的全职劳动者，年份包括1976、1980、1984、1988、1992与1996，最终获得2664474个观测值。

两步估计法的优势包括三点，第一，在地区层面上，考虑地区部门变量与误差项相关性；第二，计算系数的标准误时可以计算地区层面的误差；第三，可以对第二步方差进行分解。

 

TFP测算的基础数据来源于BRN、RSI、SIREN与DADS数据库，首先，在企业活动单元级别，按照企业活动单位标识符将SIREN与DADS进行匹配。其次，构建企业级数据集，使用企业标识符在企业层面汇总前面的企业活动单元数据集。最后，将此企业级数据与RSI和BRN合并整合企业层面信息。最终结果如下：对于1994年至2002年之间的每个企业，测算其增加值，资产价值以及产业活动单元层面不同技能组的劳动力总工作时间，1994年的观察总数为942,506，且观察数在研究期缓慢上升。此外，由于企业的资本和产出仅有企业层面的数据，且多厂企业的全要素生产率估计具有复杂性，所以只考虑单厂企业TFP的估计，且只保留雇员超过五人的公司。

 

对于TFP而言，本文采用了OP法、OLS法以及固定效应方法来测算TFP，且每种方法测算了3个不同的TFP值，第一种方式是直接求平均值，第二种方式是在回归方程中增加部门虚拟变量后求平均值，第三种方式是在回归方程中增加部门及地区层面的变量来测算。与工资测算类似，故不再赘述。此外，本文探究了不同方法测算的工资之间、TFP之间、工资和TFP之间数据的相关性，发现大都超过了90%，相关性很大。

 

05 估计结果

 

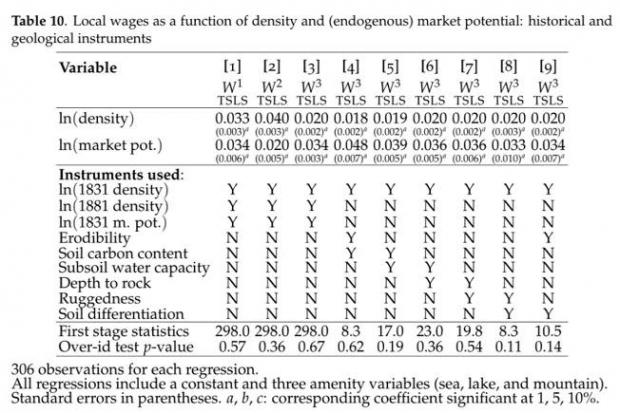
本文进行了一系列回归来探究密度与生产率之间的关系，主要分为以下几种情况，工具变量为历史变量、工具变量为地质变量、工具变量为历史变量与地质变量、工具变量为历史变量与地质变量时加入外生的市场潜能、工具变量为历史变量与地质变量时加入内生的市场潜能。工资的主要回归结果见下表：第一，密度的弹性估计值为0.048，在控制劳动力质量偏误时，系数为0.033，以此为基础，增加历史工具变量控制劳动力数量偏误进行分析时，系数变为0.027，说明劳动力质量和数量同时影响生产率，且劳动力质量带来的影响（0.048→0.033）比数量带来的影响（0.048→0.040）大。第二，无论是加入外生的市场潜能还是加入内生的市场潜能，密度系数均稳定在0.02，结果非常稳健，说明集聚经济促进了生产率的提高，详见表9和表10。第三，对比第一阶段统计量分析，发现人口密度和市场潜能的工具变量组合比地质变量和人口密度的工具变量组合更好，这可能是历史工具变量应用更广泛的重要原因。此外，TFP的回归结果与工资的回归结果基本类似，故不再赘述。

06 结论与讨论

 

本文使用法国的工资和全要素生产率数据重新评估了集聚效应，一是用工具变量方法剔除劳动力数量对估计结果的影响，并在历史工具变量的基础上增加了地质工具变量。二是用劳动力固定效应方法剔除劳动力质量对估计结果的影响。第一个发现与劳动力数量带来的内生性问题有关。总的来说，历史工具变量是较好的工具变量，地质工具变量较为复杂。但一旦回归正确设定，历史和地质工具变量会得出类似的结果，即就业密度与生产率之间的反向因果问题相对较小，将密度的影响降低了约五分之一。第二个发现与劳动力质量带来的内生性问题有关。高技能劳动力倾向于选择生产率更高的地区，因此，在工资回归分析中，本文使用工资数据的纵向维度解决这一问题，发现密度的弹性系数几乎小了一半。此外，工资包含了不可观测的劳动力特征。因此，工资回归结果更具有代表性，但工资与全要素生产率结果之间的高度相似说明结果非常可信。

 

本文的特点在于以下几个方面：第一，对因果识别问题进行了详细的分析；第二，从工资和TFP两个层面测算了生产率；第三，用固定效应方法对工资与TFP进行了分解；第四，使用不同的工具变量组合来增强计量的稳健性；第五，对数据清洗过程的介绍比较详细；第六，在论证的过程中分析了存在的问题、提出的解决办法以及相应地辩护，逻辑严密。

 

本推文由中国经济转型讨论班（CETW）供稿。

 

Abstract

 

Does productivity increase with density? We revisit the issue using French wage and TFP data. To deal with the ‘endogenous quantity of labor’ bias (i.e., urban agglomeration is consequence of high local productivity rather than a cause), we take an instrumental variable approach and introduce a new set of geological instruments in addition to standard historical instruments. To deal with the ‘endogenous quality of labor’ bias (i.e., cities attract skilled workers so that the effects of skills and urban agglomeration are confounded), we take a worker fixed-effect approach with wage data. We find modest evidence about the endogenous quantity of labor bias and both sets of instruments give a similar answer. We find that the endogenous quality of labor bias is quantitatively more important.