推文人 | 王岳龙 

论文来源：Guido.W.Imbens，“Matching method in Practice Three Examles”The Journal of Human Resource 2015

 

一、 引言

 

目前DID、RD、IV等因果识别方法在国内外应用十分广泛，香樟推文包括我本人也推送了大量上述方法的应用，但是对Matching却少有介绍，该方法在前几年国内公司金融、财务会计领域研究用的特别多，但是在实际应用中往往一知半解，存在了诸如matching可以解决内生性问题的误解，以及选择匹配的协变量和函数形式过于随意，因此本文结合微观计量大神Imbens在2015JHR的一个论文，详细介绍该方法的原理和应用。

 

二、 Matching的基本原理

 

1.Matching的本质

 

国内很多文章都说matching能解决内生性问题，一直没有查到该说法的最原始出处，但是被国人以讹传讹流传到现在，所以在这里必须强调下matching和OLS一样都属于selection on observables的方法，识别假设都是是unconfoudness或者说是conditional independent assumption，（y0,y1），此外matching还多了个overlap（共同区间假设）所谓CIA假设，就是控制住所有可观测因素x后，未观测变量不会对两组观测结果y产生系统性差异，也就是出现内生性问题。因为内生性问题意味着未观测因素是可能的confounding factor，既影响个体选择D，又影响结果变量y，即便控制可观测因素，选择性偏差仍然存在，因此我们说matching本质不能解决内生性问题。

 

2.Matching和OLS的比较

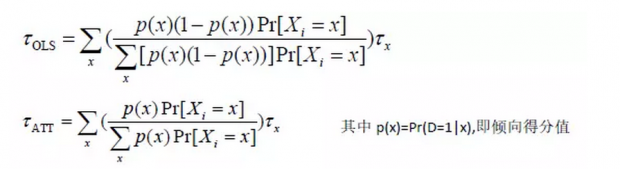
两个估计量形式十分类似，因此OLS是一种特殊的匹配方法。OLS是以条件方差p(x)(1-p(x))为权重进行加权，当p(x)=0.5时权重最大，因此它对层内两组个体数目相同的层赋予更大的权重。匹配估计是以倾向得分指数p(x)进行加权，对层内处理组个体更多的层赋予更大的权重。两个估计参数一般是不同的，只有当p(x)和τx是常数时，两者才相等。

 

3. OLS的不足和Matching的优点

 

既然matching和OLS本质是一样的，但是为什么还要在有了最简单实用的OLS基础上，再弄出一个matching方法，这两个方法各自有什么优缺点，这是一个值得关注的问题。由上式可知，OLS估计时对于倾向得分指数为0或者1的层，将赋予0权重，回归时自动丢弃那些仅有参考组或者处理组一组个体的层，因此得到的估计系数不能解释为总体的ATE。协变量匹配的好处在于匹配时，由于需要检验共同区间的要求是否满足，从而很清楚哪些样本进入匹配，从而知道是对哪部分子样本的估计，这是匹配方法相对于回归方法的优势之一。其次为了避免extrapolation和misspecification，使得OLS估计因果效应具有一致性，要求条件期望函数必须是线性，同时处理组和控制组的控制变量具有相同的分布。因此当控制变量组间差异非常大时，且数据对函数形式设定也非常敏感，OLS往往不能得到稳健的估计结果，而这些问题对matching并不存在。imbens在论文中引入一个参加NSW项目培训对收入影响的例子，通过线性和对数线性2个不同模型设定形式，显示了差异比较明显的ATT结果。

 

4.Matching的分类

 

Matching按照其寻找反事实的方法，可以分为协变量匹配和倾向得分匹配（PSM）两大类。协变量匹配是基于各变量空间距离（马氏、欧式距离），但是当样本小或者变量多时，通常难以找到与之匹配的个体。这时可以考虑采用倾向得分匹配，通过估计处理变量的影响因素方程，把多维控制变量降成一维的倾向得分值。King and Nielsen（2016）指出，倾向得分匹配将许多协变量综合成倾向得分值，由此可能导致倾向得分值接近而协变量差异更大，建议采用协变量匹配。由于协变量匹配是以分组随机实验为基础，由于考虑了协变量差异，可以保证匹配样本的平衡性。此外还有逆概率加权匹配、回归调整、核匹配方法，stata13新出的teffects命令可以很方便实现上述方法。

 

三、 Matching的规范操作步骤

 

1.设计阶段

 

Δ和样本均值差异t检验计算式很像，由于上式t检验与样本容量有关，当样本很大时，即使协变量平衡也可能出现显著差异结果，所以imbens不推荐采用。

 

如果normalized differenceΔ差异很大，需要考虑删减样本，以更好满足overlap假设。根据Crump etal(2009),保留α<e(x)<1-α的样本，其中

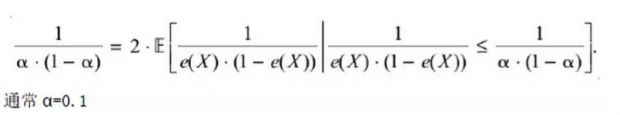
2. 补充分析：评价CIA假设

由于现实中只能观测到一个潜在结果，因此CIA假设本身无法直接被检验。Imbens(2004)和Imbens and Rubin(2015)提出了两种间接检验方法，类似DID里面的falsification test，并不是充分条件，不拒绝原假设也不能保证CIA一定成立，只是提供了暂时没有发现CIA不成立的证据，使我们有很大信心相信估计结果。

 

利用一个事实上没有受到干预影响的变量作为伪结果，用它作为潜在结果y0的代理变量，一般选择滞后的结果变量作为伪结果变量yp。如果控制X，影响潜在结果的所有混淆因素均被控制，未观测因素将不会对两组结果产生系统性影响，伪结果估计的ATE将为0。反之如果ATE显著不为0，说明仍然存在着未观测的混淆因素没有被控制，从而CIA假设不成立。

 

3.分析阶段：确定合理的函数形式

 

以PSM为例，选择哪些变量和变量形式进入logit模型估计是个十分重要的问题。变量和变量形式不同，算出来的倾向得分值自然就不同，倾向得分值不同匹配的个体就不同，从而得到不同的ATT，所以确定logit模型的形式很关键，但是这个问题在国内以往研究就忽略掉了，选择模型过于主观随意，没有经过严格检验，为此imbens提出了下列stepwise回归检验方法供参考：

 

（1）先根据相关理论和经验确定必须要加入的preslect变量（如果没有相关先验信息，则只放常数项）

 

（2）逐步加入其他变量一次项，对新增变量进行联合显著性检验的likelihood ratio test，此时临界值是Clin=1

 

（3）逐步加入二次项（平方项和交互项），同样对新增变量进行联合显著性检验的likelihood ratio test，此时临界值是Cqua=2.71

 

四、一个简单的例子

 

Imbens(2015，jhr)的论文里面原本提供了三个例子，这里选取第一个是否中彩票对日后劳动收入影响的例子进行重点讲解。

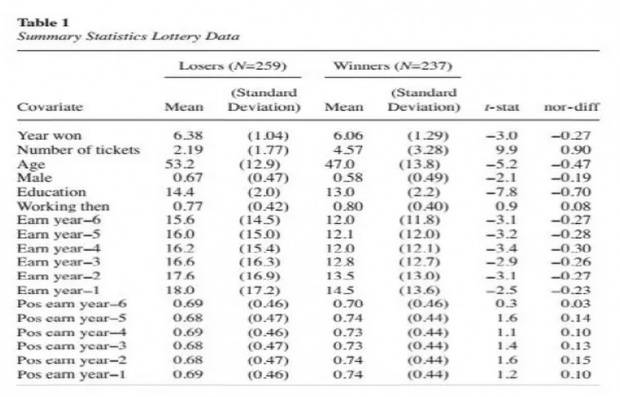
首先对中彩票和没有中彩票的两组人进行了分组的统计描述，虽然理论上我们认为中彩票似乎是个随机事件，但是从统计分析结果来看，情况不完全是这么回事情，从均值差异检验来看，中彩票的人平均看来每周买彩票的次数更多、年纪更小、更多是女性、教育程度更低、之前6年的收入也越低。此外Δ也比较大，说明如果直接用原始数据匹配，overlap不大容易满足，匹配效果可能不会太好。为了比较，作者还是先直接用原始数据进行了匹配。

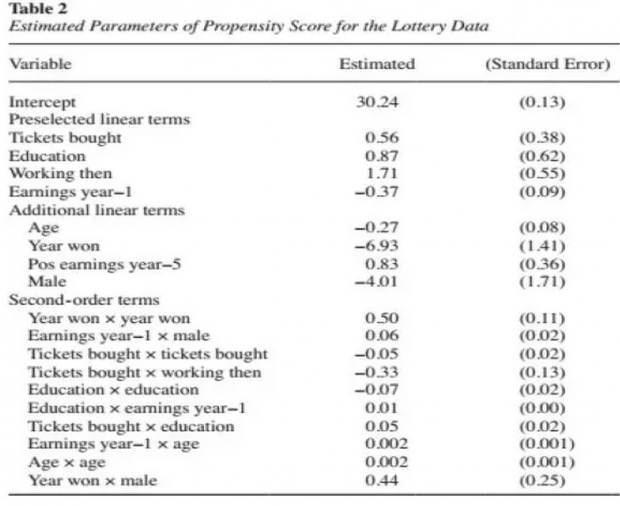
作者在估计倾向得分方程时，先将过去一周买票次数、教育程度、是否有工作、去年一年收入作为preselected变量放入模型，然后经过上述逐步回归检验，确定了上述变量进入了最终baseline模型。

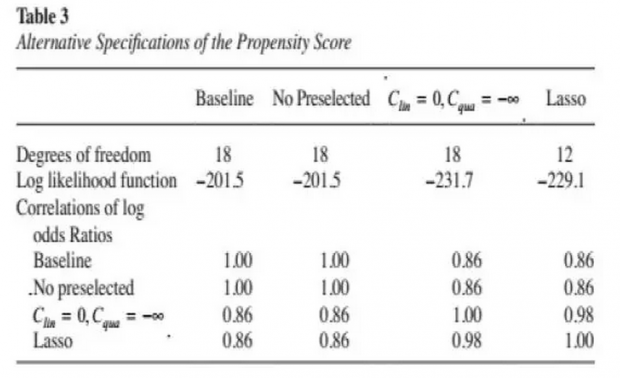
在上述模型基础上，imbens又进行了其他几个备选模型检验，表三第二列是没有任何preselected变量，完全依靠逐步回归检验情形。第三列是只放一次项情形，最后一列是根据lasso回归情形。

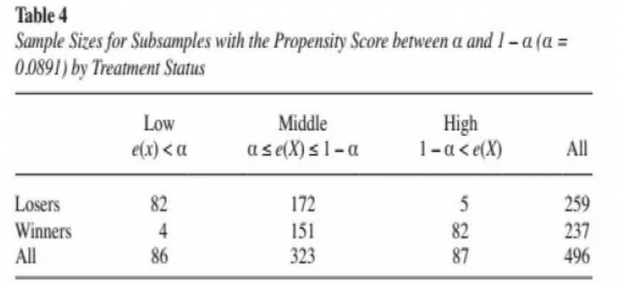
通过将α设置为0.089，将参考组中倾向得分值低于0.089和高于0.911的分别82个和5个样本，作为离群值删去，同理处理组中向得分值低于0.089和高于0.911的分别4个和82个样本也作为离群值删去，最后得到包括151个处理组和172个参考组在内的323个样本。

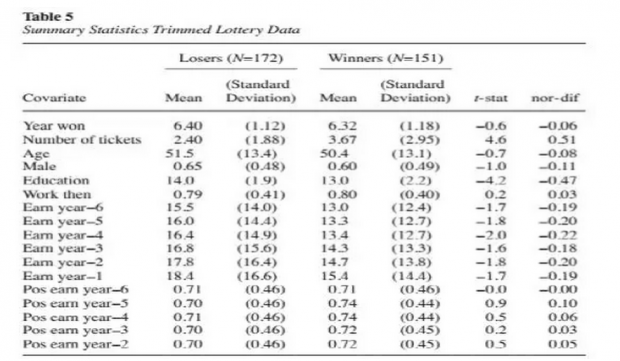
对经过trim处理后的323个样本又进行了统计描述，如上表5所示，各变量无论是组间均值差异t检验还是normalized difference都比之前小了许多，说明此时样本十分平衡，类似于通过了rct的变量平衡性测试，得到了一个类似随机实验环境，可以进行匹配。

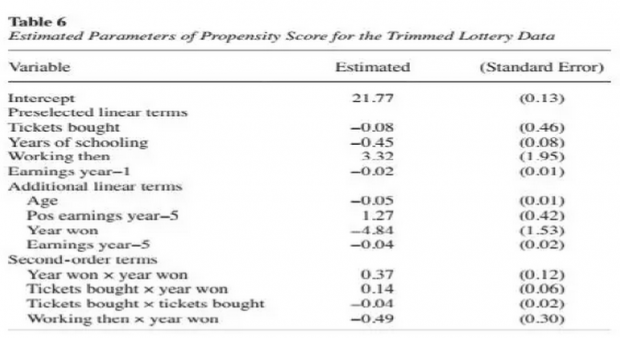
在该trim样本基础上，又重新估计了倾向得分方程，我们发现此时进入最终baseline模型的变量与之前有明显不同，主要是少了许多二次项。

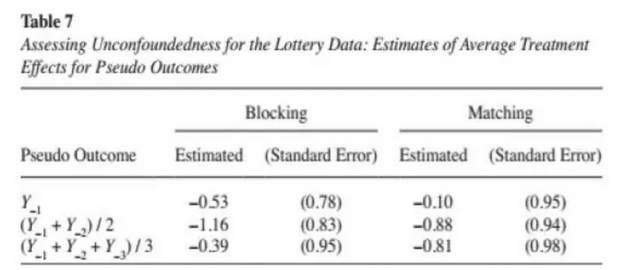
对trim后样本，接着又分别利用过去三年内的平均收入作为伪结果，对CIA假设进行了检验，结果发现无论是分组（blocking）匹配还是直接匹配，估计结果都不显著，从而暂时没有发现存在不可观测因素干扰。

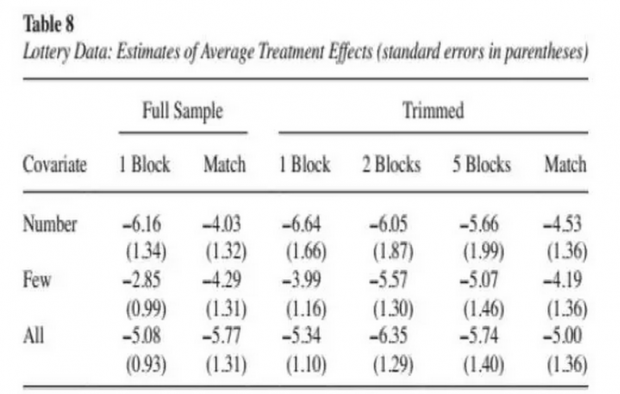
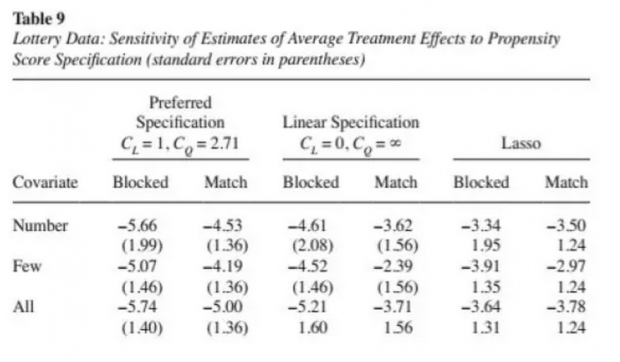
上述两表估计结果表明，通过变换各种估计和匹配方法，都得到了显著为负的稳健性结果。上面这个例子，展现了一个标准的matching所需要的全部规范流程，对比国内之前研究，会发现我们之前研究是多么的不足。

 

五、小结

 

在过去的三年中，我陆续推送了包括IV、DID、RD在内许多推文，再加上今天这个matching的推文，基本上覆盖了目前微观应用计量经济学各种主要方法，下面我再对上述方法做个简单小结：

 

共同点：通过识别策略的设计，使得观测研究近似于随机实验。

 

区别：

 

OLS（匹配）：识别条件是CIA假设（条件均值独立假设），以可观测的控制变量为条件（selection on observables)，干预的分配是分层随机实验。如果CIA条件不满足，表明只根据可观测变量分层，无法保证干预分配独立于潜在结果，仍然有其他未观测因素影响干预的分配，也就是通常所说的（selection on unobservables)

 

IV:非依从的随机化实验，干预的随机化分配是工具变量，个体实际接受的干预状态是内生处理变量，利用干预分配的随机性可以识别出受工具变量影响的个体的因果效应（LATE）。识别条件是IV的排他性假设。

 

DID（FE）：增量上的分层随机实验，通过差分或者去均值的方法消除不随时间变化的未观测的混淆因素影响，识别条件是平行趋势假设。

 

RD：断点附近的随机实验，识别假设是局部随机化假设，即个体没有精确控制断点的能力，使得断点附近个体具有高度相似性。

 

RCT：完全随机化实验，个体是否接受干预完全随机，从而可观测因素和不可观测因素在组间是均值无差异的，识别假设是独立性假设（变量平衡性测试）