阅读:0
听报道
推文人 | 张寓
原文信息:Dimmock, S.G., Kouwenberg, R., Mitchell, O.S., and Peijnenburg, K., 2015, Estimating ambiguity preferences and perceptions in multiple prior models: Evidence from the field. Journal of Risk and Uncertainty, 51, 219-224
前言
在讨论这个问题之前,我们有必要先明确风险(risk)、模糊(ambiguity)以及不确定性(uncertainty)的关系,因为这三者的关系在经济学的不同领域甚至是不一样的。风险指的是,未来某一事件的所有可能的结果的概率是已知的,换句话说,未来某一事件的结果的分布是已知的。但是在现实生活中,我们很难说一个人已知某件事情的分布,比如说我们很难明确知道未来房价或者股票上涨10%的可能性有多少。所以退而求其次,我们需要对风险进行一个更符合实际的定义,即人们可以对未来发生的某一事件形成唯一的先验分布。这里的先验分布并不一定是事件不同结果发生的真实分布,但只要个体能形成唯一的先验分布,我们即说这个个体对未来这一事件仅仅感受到了风险。而模糊则是另一个定义,最严格的定义是:人们不知道未来某一事件的分布是什么。所以通常如果我们问一个人:你觉得房价明年上涨10%的概率有多少?如果对方的回答是“不知道”,那么我们则说他感受到了模糊。而不确定性的定义则是分领域而言了。在很多宏观的动态一般均衡模型中,不确定性其实就指的是风险,比如在模型中假设短期收入震荡符合唯一一个分布,这其实是风险的定义,但是文章中则会称之为不确定性。而在一些实证研究中,不确定性其实指的就是模糊,比如经济或政策不确定性对企业或政府行为的研究。Guidolin and Rinaldi (2013)这篇综述也提到过,目前很多的文献总是将不确定性和模糊相混用。包括发表本文的期刊Journal of Risk and Uncertainty中的uncertainty可能也是被当做模糊的定义。但在Knight (1921)“Risk, Uncertainty and Profit”这本书中,风险被称之为一种“可测量的不确定性”,但还存在另一种“不可测量的不确定性”还没有被明确概念化,而这种不可测量的不确定性实际上比风险还要普遍存在。在这本书之后,这种“不可测量的不确定性”在一系列金融文献中被定义为模糊。由此可见,如果从这本书的角度出发,不确定性实际上包含了风险和模糊。但考虑到很多学者和读者的用法和习惯, 本文目前也将不确定性和模糊当做同样的定义,不过笔者其实是支持Knight (1921)将这三者区分开来进行定义的。
近些年来很多的论文在研究经济或政策不确定性(模糊)是如何影响企业或政府行为的,之所以这些研究忽如一夜春风来,很重要的一个原因就是人们找到了量化不确定性的方法。比方说利用业内专家对未来某一事件的预测的差异程度来衡量。但是用这种方法衡量不确定性只能得到一个时间序列数据,而且无法得知普通大众个人到底对未来的经济发展或政策感受到了多少不确定性。Dimmock et al. (2015) 这篇文章则是提供了一个实验的思路,来估计不同的实验个体对一项赌博游戏感受到了多少不确定性(模糊)。由于本篇论文所用的术语是模糊,因此该推文也沿用模糊的用法,但读者需明白,此处的模糊也是大家所认为的不确定性。
文章的思路是首先要找到一个指标来衡量模糊。之前我们说过,模糊指的是不知道某个事件的分布。但是这个定义有一个弊端,就是“模糊”仅仅是一个二分类变量,知道或者不知道。那么有没有可能找到一个连续变量来衡量人们究竟感受到了多少模糊呢?经济学家们想到一个办法:人们不知道 未来事件的分布,可能是因为人们对这一事件感受到了太多的先验分布,以至于他们无法形成一个唯一的先验分布。但即便在这种情况下,如果我们假设每个人都有一个“基准先验分布(p)”,那么个体相信这个基准分布的程度(1-d)则可以用来衡量人们感受到了多少模糊:如果一个个体100%相信这个基准分布,那么他其实就只有一个先验分布,也就是说他只感受到了风险,而并没感受到模糊;如果一个个体只是50%相信这个基准分布,而另外50%的置信则是其他分布,那么他明显就感受到了一定程度的模糊。所以本文的目的之一是测出对基准分布的置信程度(1-d)。
除了估计对模糊的感知以外,本文另一个目的还要估计对模糊的偏好程度,即有多么地喜好/厌恶模糊,就像人们对风险是有不同偏好程度的。本文采用的是a-MaxMin模型,这个模型中的a是一个介于0到1的数字,它被用来衡量对模糊的偏好,越接近1则表示越厌恶模糊;反之,越接近0则越喜好模糊;当a等于0.5的时候,则表示模糊中性。所以本文的另一目的是测出对模糊的偏好程度a。
方法
文章通过实验数据来得到想要的结果。首先,实验要求所有被试者进行一个赌博游戏,被试者可以选择在两个环境中的一个进行这个赌博,即“模糊的环境”还是“不模糊但是有风险的环境”。“模糊的环境”指的是被试者不知道赌博获胜的概率,“不模糊但是有风险的环境”指的是被试者明确知道赌博获胜的概率 。被试者在进行选择之前会被告知,在他们选择完一个环境进行这个赌博后,一个球会被随机地从她所选择的环境中抽出来,如果这个球是紫色的,那么该被试者会赢得15美元,如果是橙色球,则什么也得不到。
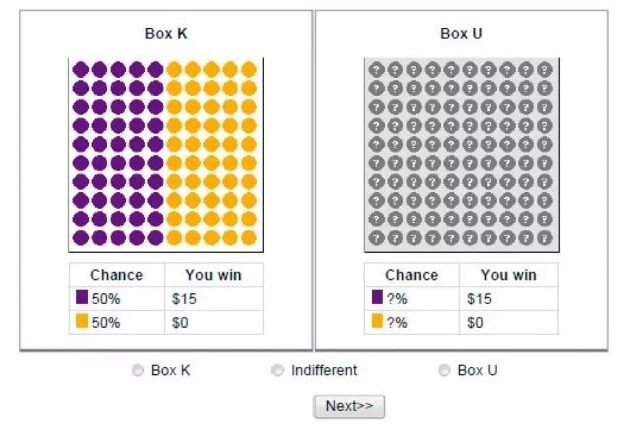
该实验包含了三组重复试验,分别进行了 “基准获胜概率(p)”为50%、10%和90%的实验,每一组重复试验都包含多轮。上图所示的是基准获胜概率为50%的实验的第一轮:Box K中,被试者明确知道获胜的概率是50%。如果一个被试者选择Box K进行游戏,那么说明他更喜欢有明确获胜概率的环境,即厌恶模糊;如果选择Box U进行游戏,那么说明他更喜欢模糊的环境,即喜好模糊;如果选择Indifferent,说明他并不偏好其中一个,那么他对模糊的偏好是中性的。假设一位被试者在第一轮游戏中选择了Box K,那么下一轮,他所面临的Box K中已知的获胜概率则会被降低到25%后再进行游戏,即如下图。
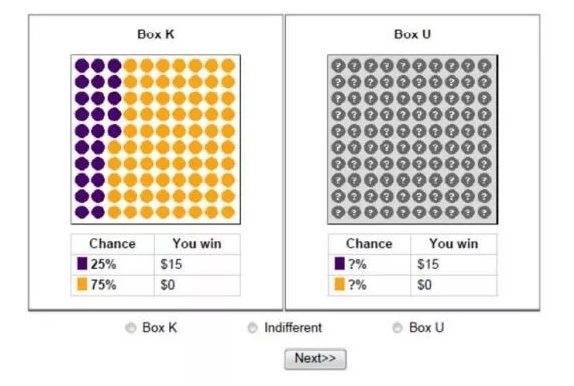
如此实验将进行多轮,直到该被试者选择Indifferent,即对两个环境没有偏好了。此时,Box K中的获胜概率被定义为“匹配概率”,也就是使得该被试者对模糊与否的环境没有偏好的Box K中的获胜概率。举个例子,如果一个被试者在此项实验中的第一轮选择了Box K,第二轮中选择了Indifferent,那么他在“基准获胜概率为50%”的实验中的匹配概率为25%。
除了基准概率为50%的情况外,该实验还进行了基准获胜概率分别为10%和90%的重复试验,每一个实验都可以得到一个被试者的匹配概率。而该论文通过一系列的数学推导,可以得出:在参数d和a下,匹配概率是基准概率的一个线性函数,换句话说,只要我们通过上述三组实验观测到每个人的基准获胜概率及其所对应的匹配概率,就可以通过回归的方式估计出该线性函数中的参数,从而根据数学推导计算出d和a。
结果
最终的实验数据显示,人们对该赌博游戏所感受到的模糊为0.6,即人们60%的程度相信实验所提供的基准获胜概率是准确的。除此之外,文章发现:男性、白人、有较多数量孩子的被试者、高受教育人群以及有更多金融知识的人会感受到更多的模糊。另外,人们则对这个游戏有弱模糊厌恶,因为所估计的a=0.53。而老年人、男性和高受教育人群则更加厌恶模糊。
讨论
当然,目前这个文章只是估计个人对赌博游戏所感受到的模糊(不确定性)及其厌恶模糊的程度,如何将其运用到现实生活中的例子,比如普通大众或者个体企业对未来经济或政策感受到了多少模糊,还需要以此文为基础进行延伸。当能够对具体的现实事件估计模糊后,才能更好地研究什么因素能够影响人们所感受到的模糊,以及在人们感受到模糊后会采取什么行为。
Abstract
We develop a tractable method to estimate multiple prior models of decision-making under ambiguity. In a representative sample of the U.S. population, we measure ambiguity attitudes in the gain and loss domains. We find that ambiguity aversion is common for uncertain events of moderate to high likelihood involving gains, but ambiguity seeking prevails for low likelihoods and for losses. We show that choices made under ambiguity in the gain domain are best explained by the a-MaxMin model, with one parameter measuring ambiguity aversion (ambiguity preferences) and a second parameter quantifying the perceived degree of ambiguity (perceptions about ambiguity). The ambiguity aversion parameter a is constant and prior probability sets are asymmetric for low and high likelihood events. The data reject several other models, such as MaxMin and MaxMax, as well as symmetric probability intervals. Ambiguity aversion and the perceived degree of ambiguity are both higher for men and for the college-educated. Ambiguity aversion (but not perceived ambiguity) is also positively related to risk aversion. In the loss domain, we find evidence of reflection, implying that ambiguity aversion for gains tends to reverse into ambiguity seeking for losses. Our model's estimates for preferences and perceptions about ambiguity can be used to analyze the economic and financial implications of such preferences.

话题:
0
推荐
财新博客版权声明:财新博客所发布文章及图片之版权属博主本人及/或相关权利人所有,未经博主及/或相关权利人单独授权,任何网站、平面媒体不得予以转载。财新网对相关媒体的网站信息内容转载授权并不包括财新博客的文章及图片。博客文章均为作者个人观点,不代表财新网的立场和观点。




 京公网安备 11010502034662号
京公网安备 11010502034662号 