阅读:0
听报道
推文人 | 詹江
原文信息:Garin, Julio, Michael J. Pries, and Eric R. Sims.2018."The Relative Importance of Aggregate and Sectoral Shocks and the Changing Nature of Economic Fluctuations."American Economic Journal: Macroeconomics,10(1): 119-48.
摘要
随着总体和部门冲击相对重要性的转变,美国20世纪80年代中期总体波动率呈现下降趋势。利用部门工业生产数据的主成分分解,作者证明总体冲击对总产出差异的贡献率从1967 - 1983年的约70%下降到1984 - 2014年的约30%。本文构建了一个包含两部门和劳动力成本再分配的“岛屿”模型,以研究这种冲击相对重要性的变化如何改变标准的商业周期变量。通过校准总体和部门生产率,来匹配1984年前后时段的整体产出波动和冲击的相对重要性,作者发现1984年以后的平均劳动生产率周期显着下降与部门冲击关联更大,并且与其他一些商业周期变化也保持一致。
1.引言
对于推动经济波动的冲击的本质探讨对政策制定者有重要意义。与卢卡斯(1977)的著名论断“商业周期都是相似的”相反,“自20世纪80年代初以来,美国商业周期的行为看起来与卢卡斯认为的的二战后时期有很大不同。一个明显变化是产出和其他经济总量波动的显着下降,这种波动性的明显下降被称为“大缓和”(Great Moderation),对造成这一时期的经济波动显著差异的解释一直是大量研究所关注的问题。
2.数据
本文使用的月度样本数据以1967年开始,在2014年7月结束。其中主要关注的是构成工业生产总指数的12个主要部门。这些部门包括“最终产品”和“非工业用品”下的第二级子类别,“原材料”下的第二级子类别以及全部制造业行业。为说明这12个部门是否具有代表性,作者使用就业份额作为权重,通过部门IP增长率得到合成的加总IP序列。合成序列(synthetic series)的增长率与实际加总IP的增长率之间的相关性为0.99。为了评估本模型如何很好地解释这些观察到的商业周期的变化,作者对两个时间段样本进行了模拟,一个用于表示1967-1983子样本,另一个用于说明1984 - 2014年的子样本。
3.模型
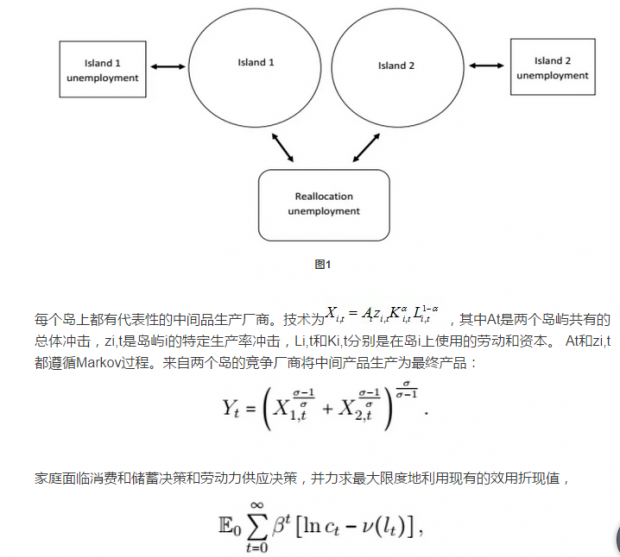
本节借鉴了卢卡斯和普雷斯科特(1974)的一个劳动力再分配的岛屿模型,该模型具有特定岛屿生产率冲击和总体生产率冲击。这些岛屿可以代表不同的部门,地区,行业或职业。尽管将分析扩展到多个岛屿在概念上会很简单,但为了便于计算,本文只关注两个岛屿的情形。图1描绘了模型经济的基本结构。这两种冲击会对总体就业,生产率和产出产生不同的反应。考虑一个负面的总体冲击,保持两个岛屿的相对生产率不变。不可分割的劳动和就业分配假设意味总体生产率仍然较低时,两个岛屿的就业人数将下降。但是,当总体生产率恢复时,这些失业工人很快会在同一个岛上重新就业。整体来看,就业、产出和生产率全部下降,然后迅速恢复。实质上,在没有再分配冲击的情况下,该模型成为Hansen(1985)不可分割劳动的一般均衡模型的两部门版本。

4.实证结果
对于实证结果重点关注以下统计量:产出的标准偏差,效率楔和劳动楔;以及产出与平均劳动生产率之间,效率楔与总产出之间以及劳动楔与总产出之间的相关性。在数据中,产出被定义为NIPA账户的实际国内生产总值,非农业部门的人均工作小时数。在模型和数据中,本文借鉴了Chari,Kehoe和McGrattan(2007)使用的效率和劳动力楔子的定义。
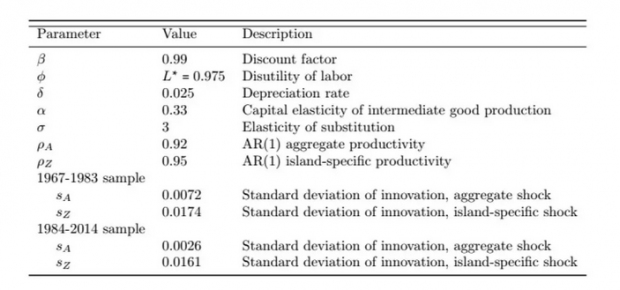
进一步讨论之前,首先需要对模型参数进行校准。这些参数包括:β贴现因子;φ是关于劳动力负效应的标度参数;σ来自两个岛屿的替代中间投入的弹性;δ,资本折旧率;λ,这个参数决定了两个岛屿之间重新分配的速度;ρ是控制总体和岛特定生产率冲击的随机过程的参数。
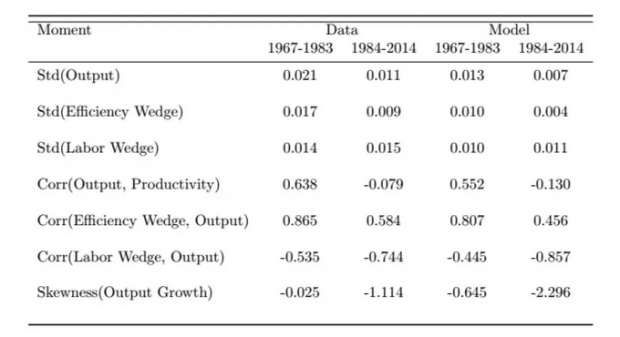
具体结果如下表所示。就波动性而言,作者发现产出的波动性在大缓和时期是前一时期(1967-1983)大约一半,同样,效率楔也是前一样本期的波动性的一半左右,有趣的是,在相关系数方面,早期产出与劳动生产率的相关性呈显着正相关(相关系数为0.64),效率楔也具有强周期性(与产出相关系数为0.86),而劳动力楔子是反周期性的(相关系数为-0.53),从84年之前到之后,劳动生产率从强周期性转变为轻度反周期性(在后一时期与产出相关系数为-0.08)。虽然效率楔与产出的相关性反映的的周期性略有下降(从0.865到0.584),但它仍然是顺周期的,它与产出之间的相关性下降程度并不像劳动生产率和产出之间的相关性下降那么大。在后一时期样本中,劳动楔呈现出更加强烈反周期性(与产出相关系数为-0.74)。在1984年后的样本中,产出增长的偏度变化显著,从不明显到变为明显的左偏。
5.结论
首先在本文的主成分分析中,对于工业生产数据的12个部门,作者从部门产出增长率中提取第一个主成分,以捕捉各部门共同的变动特征。作者将这个第一主成分中的变动解释为源于总体或普通冲击的波动。与第一主成分正交的残差分量与部门冲击相关联。加总的工业生产增长率的方差分解表明,在1967 - 1983年的子样本中,总体冲击(即第一主成分)的贡献占方差的70.9%,而在1984 - 2014年的子样本 ,总体冲击的贡献仅占方差的31.5%。此外,总体冲击的贡献下降本身完全解释了两个时期内工业生产波动的整体下降。也就是说,总体的波动性下降了,而部门冲击的波动性大致保持不变。
然后,本文使用重新分配劳动力的“岛屿模型”来研究这种不断变化的冲击结构是否可以解释美国经济波动性质发生的若干显着变化。本文区分了加总冲击和重新分配导致的部门特定冲击,并发现在两次冲击中,产出波动的对称程度有所不同。相比之下,重新分配的冲击总是导致就业减少,从而导致产出减少,没有相应的上升。因此,当由于重新分配的冲击而产生的波动时,产出增长率呈负向偏斜,但当冲击总量增加时,产出增长率并没有呈现显着的偏度。
虽然这两种冲击本身对波动的本质有着完全不同的含义,但实际上观察到的波动是由重新分配冲击和总冲击两者共同作用的结果。结果表明,1984年以后,劳动生产率从1984年以前的强周期性曲线(产出与劳动生产率之间的相关系数为0.64)变为略微反周期曲线(相关系数为-0.08)。其次,测量效率楔的波动率下降(标准差从0.017下降到0.009),而劳动楔的波动性基本不变(标准差从0.014到0.015)。第三,产出增长率呈现出更加负倾斜程度增加,偏度从-0.025下降到-1.114。这些结果与Foerster,Sarte和Watson(2011)的相关工作基本一致。
Abstract
A principal components decomposition of sectoral IP data reveals that the contribution of aggregate shocks to the variance of aggregate output declined from about 70 percent in the period 1967–1983 to about 30 percent after 1983. We develop an "islands" model with two sectors and costly labor reallocation to investigate how this change in the relative importance of shocks alters business cycle moments. A version of the model with relatively more important sectoral shocks results in a sizeable decline in the cyclicality of labor productivity and is consistent with changes in several other business cycle moments observed in the data.

话题:
0
推荐
财新博客版权声明:财新博客所发布文章及图片之版权属博主本人及/或相关权利人所有,未经博主及/或相关权利人单独授权,任何网站、平面媒体不得予以转载。财新网对相关媒体的网站信息内容转载授权并不包括财新博客的文章及图片。博客文章均为作者个人观点,不代表财新网的立场和观点。




 京公网安备 11010502034662号
京公网安备 11010502034662号 