图片来源：https://www.bigbigwork.com/tupian

原文信息：Gallagher, J. (2014). Learning about an Infrequent Event: Evidence from Flood Insurance Take-Up in the United States. American Economic Journal: Applied Economics, 6(3), 206–233.

01

引言

一直以来，经济学家们对外生事件，如自然灾害对个体风险信念的影响有着浓厚的兴趣，其受到关注的一个原因是，经济主体似乎在灾难刚发生时会产生过度反应。最近的一些文献表明，人们是根据以往的自然灾害逐渐累积形成信念进而采取经济行为，这种变化与贝叶斯学习模型相一致。

本文使用事件分析框架比较洪水发生前后保险的购买量来测度美国家庭的信念变化。研究结果发现：相较于没有经历洪水灾害的社区，经历洪水灾害的社区在保险覆盖率立即上升，而后稳定下降，直至9年后不再显著。进一步的研究发现，反复经历洪水灾害的地区会重复出现同样的过程，即家庭并不会根据最新的洪水灾害情况来评定洪水所造成的损失。

背景

02

（1）国家洪水保险计划（NFIP）

NFIP于1968年设立，其利率定价依据历史洪水数据、水文模型和详细的社会洪水地图。工程和历史数据用于判断地区预计产生的洪水损失，为了简化利率设定流程，NFIP指定了有限数量的国家洪水区，不同洪水区对应不同的保险费率。

家庭每一年都对是否购买洪水保险进行决策。洪水保险单由私营保险公司按NFIP规定的保险费率出售。NFIP的保费费率不受家庭房屋是否被洪水淹没的影响，并且在本文所包含的样本区间内，这些洪水区的保险费率基本没有发生变动。这保证了家庭信念的变动并非来自保险费率的变动。

（2）总统灾难声明（PDD）

1950年的《救灾法》确立了PDD制度。PDD系统是在大型自然灾害发生后请求和接受联邦援助的一项正式流程，该计划对遭受自然灾害的地区提供公共支持和个人支持，包括清除废墟，修复基础设施，并协助重建公共建筑等。

本文使用PDD中事件作为地区洪水灾害的来源，包含了洪水灾害地理位置、成本等信息。1990-2007年的面板数据中，NFIP覆盖的区县有2704个，占美国所有区县的大约86%，覆盖了全美人口的约92%。这其中几乎每个县都至少遭受过一次PDD洪灾，一个县发生PDD洪水次数的中位数为3次。Figure 1展示了1990-2007年全美遭受PDD洪灾的分布情况。

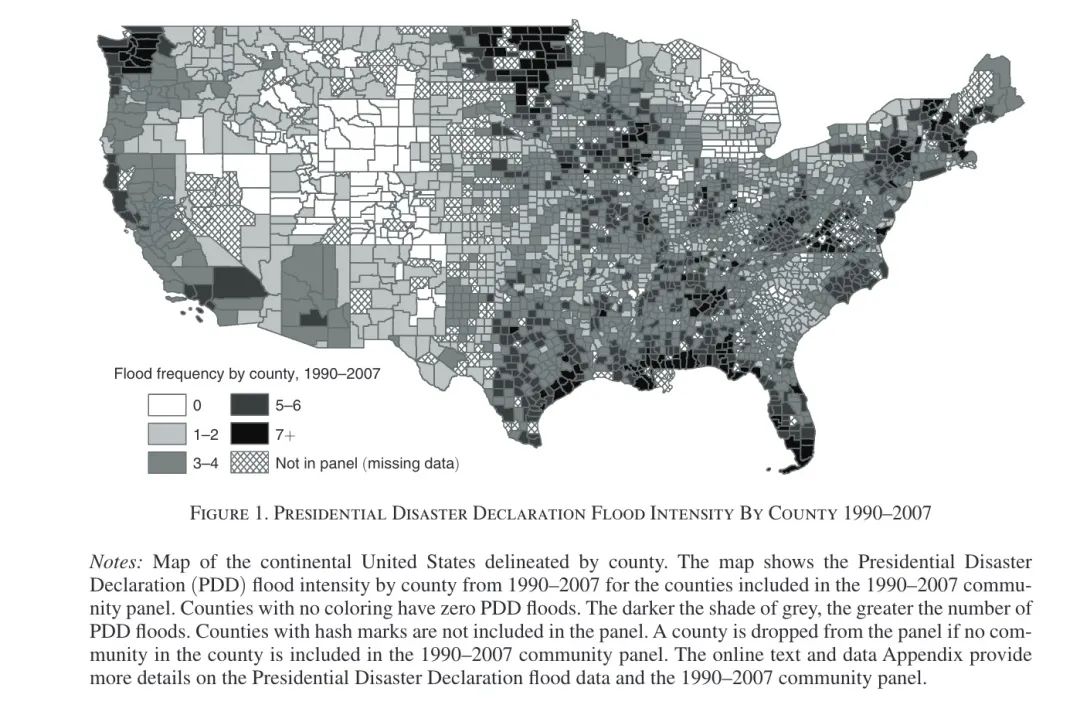
PDD洪水记录在区县层面，而同一个区县内并非所有的社区都经历了洪水灾害，因此，本文根据1990-2007年PDD项目中公共救助中记录的地址来判断某小区是否遭遇了洪水灾害，其中PDD洪水灾害中约有32%的社区经历了洪水灾害。此外，本文假定1958-2007年某个小区受到洪水灾害的概率是恒定的，这保证了保险费率设定的一致性；同时假定了PDD洪水不存在年度序列相关性，并进行了相关检验。

03 

模型和结果

（1）模型构建

本文使用事件分析框架来分析大范围的洪水灾害对家庭洪水保险购买的影响，下式（1）为本文的主要回归方程：

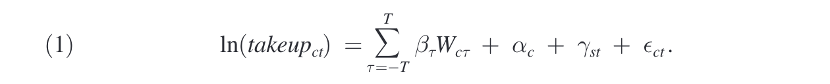
其中，ln(takeupct)表示社区c在时间t购买保险家庭数量的对数；Wcτ是一项虚拟变量，Wc0为1表示区县c在日历年遭受了洪水灾害；为1表示区县在年经历了洪水灾害。回归模型中还包含了社区层面的固定效应，州-年份固定效应和随机误差项，聚类至州层面。

此外，本文还考虑了临近社区是否遭遇洪水对本社区的影响，因此在回归中加入了临近社区是否遭遇洪水灾害的指示变量，构造回归模型如下：

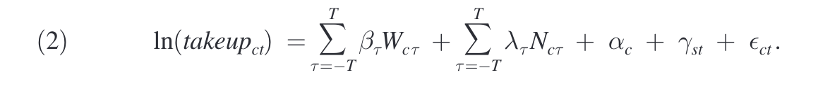
（2）估计结果

1. 遭受洪水袭击的社区

Figure 2中画出了1990-2007年之间数据面板的回归系数。横轴表示时间，0表示某社区遭受PDD洪水灾害。-10,…,-1表示洪水灾害发生前，1,…,10表示洪水灾害发生后，结果标准化至洪水发生的前一年。结果发现，在洪水发生之前，未来遭受洪水地区和未遭受洪水灾害地区之间购买保险的数量没有显著差异，而发生洪水灾害后，这些社区购买保险的数量显著增加，并且在洪水灾害后的9年依然存在显著正向效果。

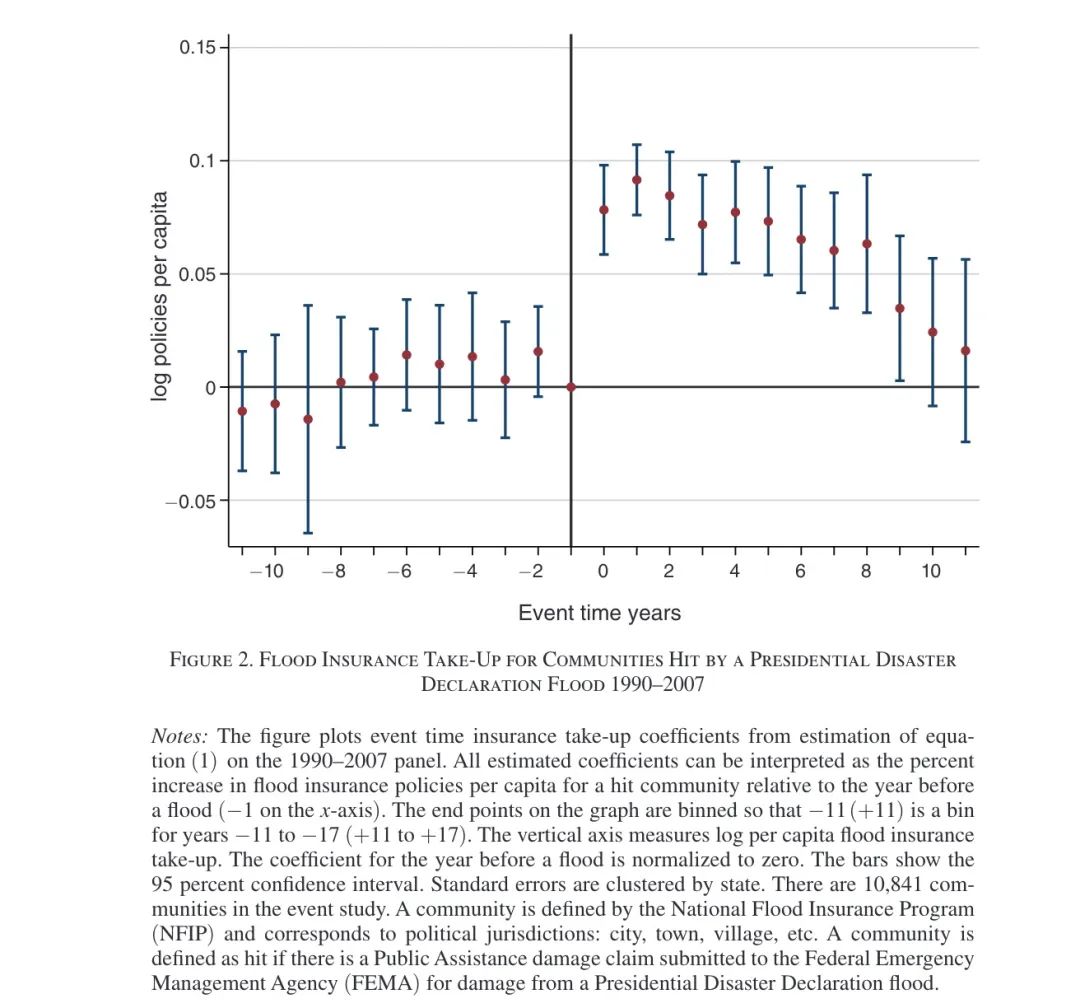
Figure 3中绘制了第二个公式设定下的回归结果，考虑临近社区是否遭遇洪水对本社区的影响。可以发现：存在洪水灾害的县，未受灾社区的保险覆盖率增加了2-3%，这种效果保持了近5年。

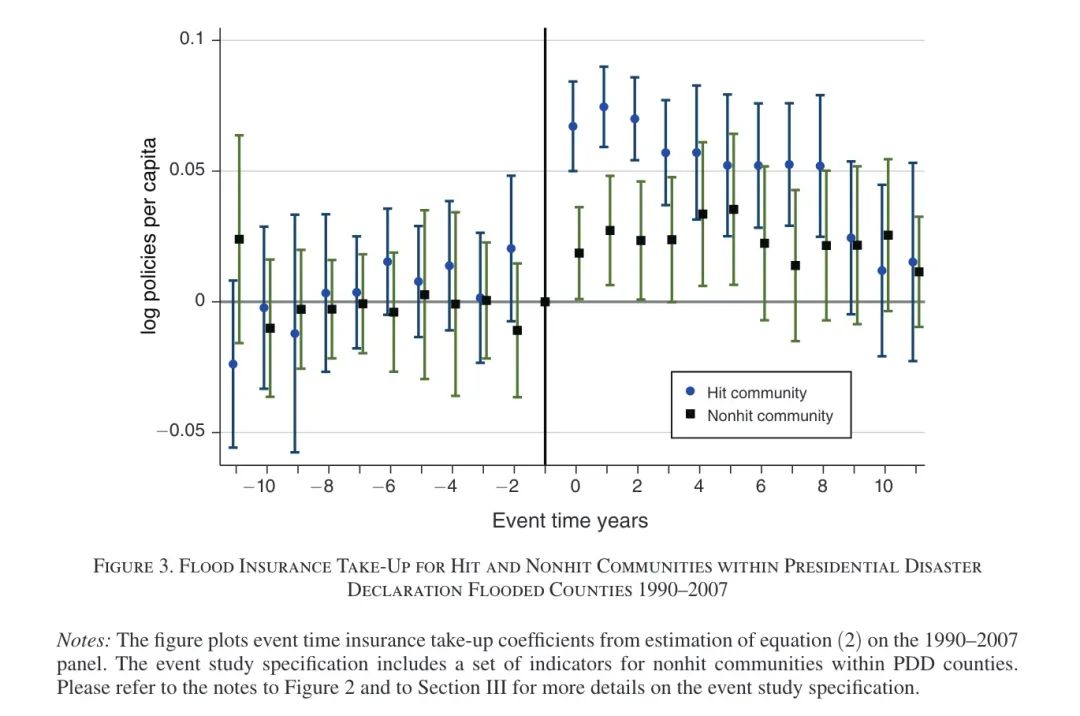
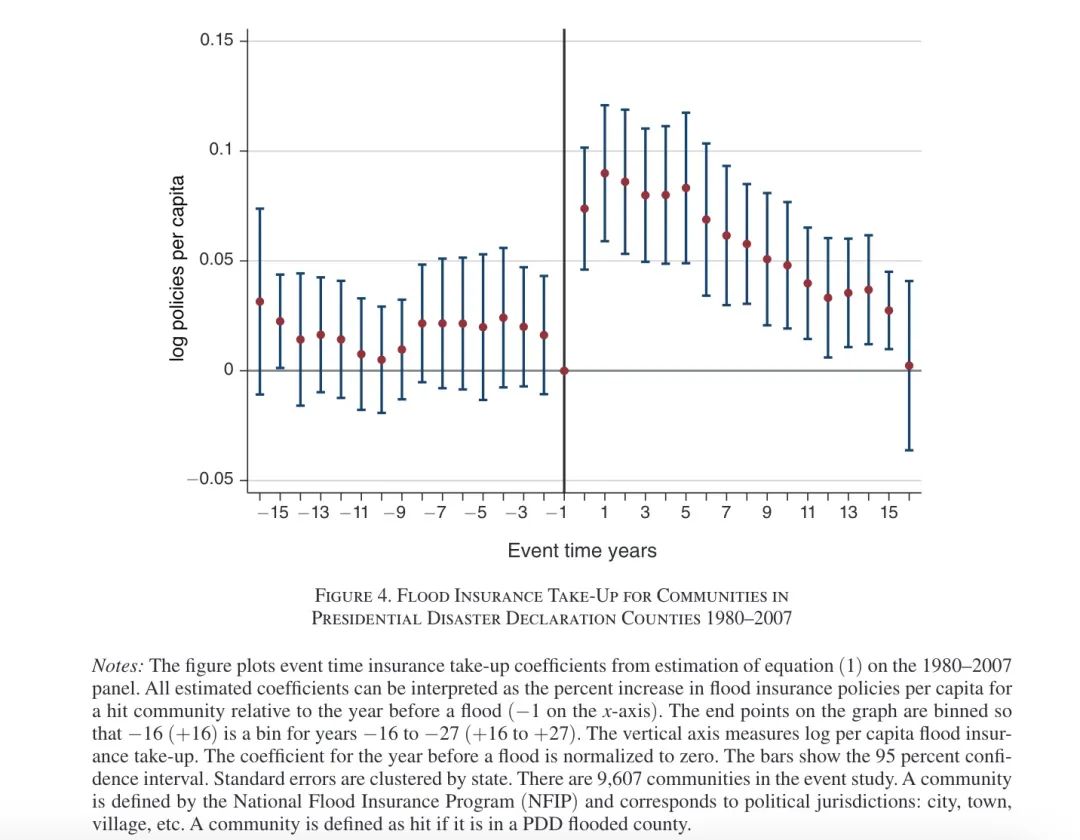
同时，本文还考虑增加样本数据，以控制在此之前发生的PDD洪水的滞后效应。结果见Figure 4中所示。

洪水成本：家庭可能会根据新的洪水灾害来更新他们对洪水损失的预期。因此，本文根据洪水成本进行分组，分别按照公式一进行回归。结果表明家庭对不同洪水提供的信息的理解是一样的，并不会利用新的洪水来了解预期的洪水损失。

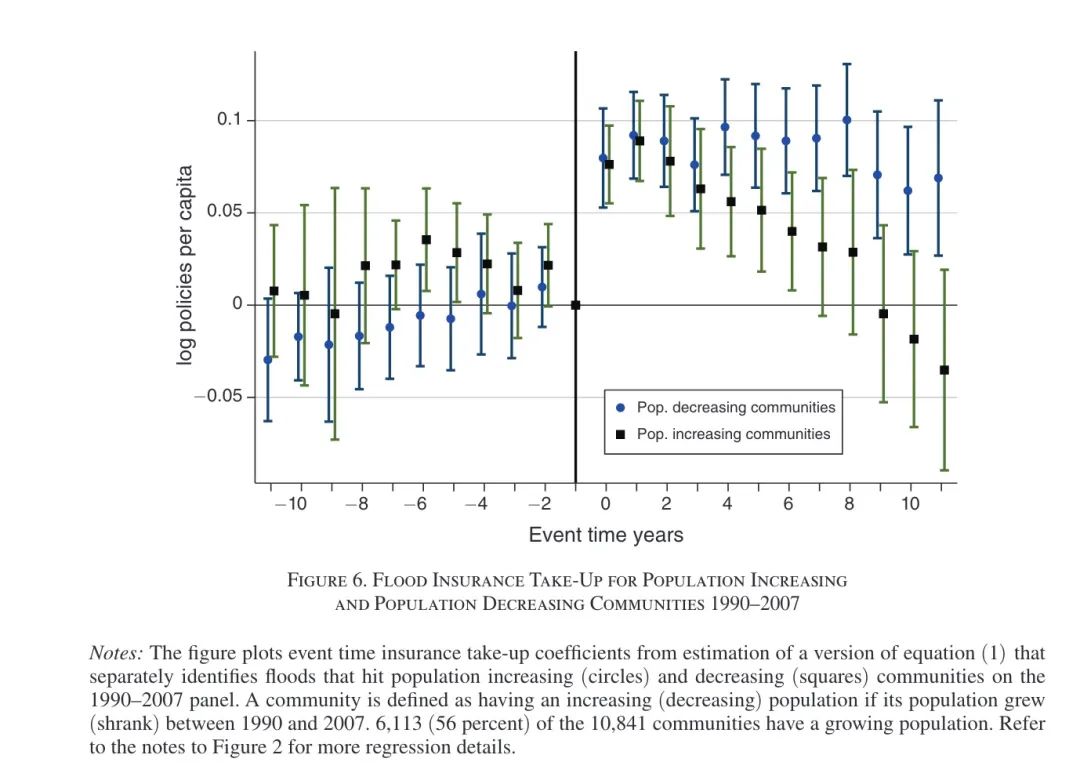
移民：移民也许在一定程度上能够解释洪水灾害后保险购买的变动情况，在有充分劳动力流动的情况下，并且新流入的人口不了解对本社区过去发生的洪水灾害，或者说获取这类信息的代价很高，购买保险可能会相应下降。首先，本文将社区划分为社区人口流入增加和社区人口流入减少，如Figure 6所示，人口流入增加的社区在洪水灾害后购买保险的数量立即减少，而人口流入下降的社区相对平缓的多。其次，本文也提供了证据表明洪水后保险购买增加的系数点估计值在低人口迁入县更大，但高人口迁入县没有显著增加。

社区层面的保护措施：社区可能会在遭受洪水后采取保护措施，以减少未来发生洪水灾害的可能性。如果发生这种情况，居民可能更倾向于在洪水之后的几年里，在社区范围内的结构变化完成之前，进行自我保险。但相关的证据表明社区范围内的保护措施并不能解释Figure 2和Figure 4中保险购买模式的变动。

2. 临近社区遭受洪水灾害

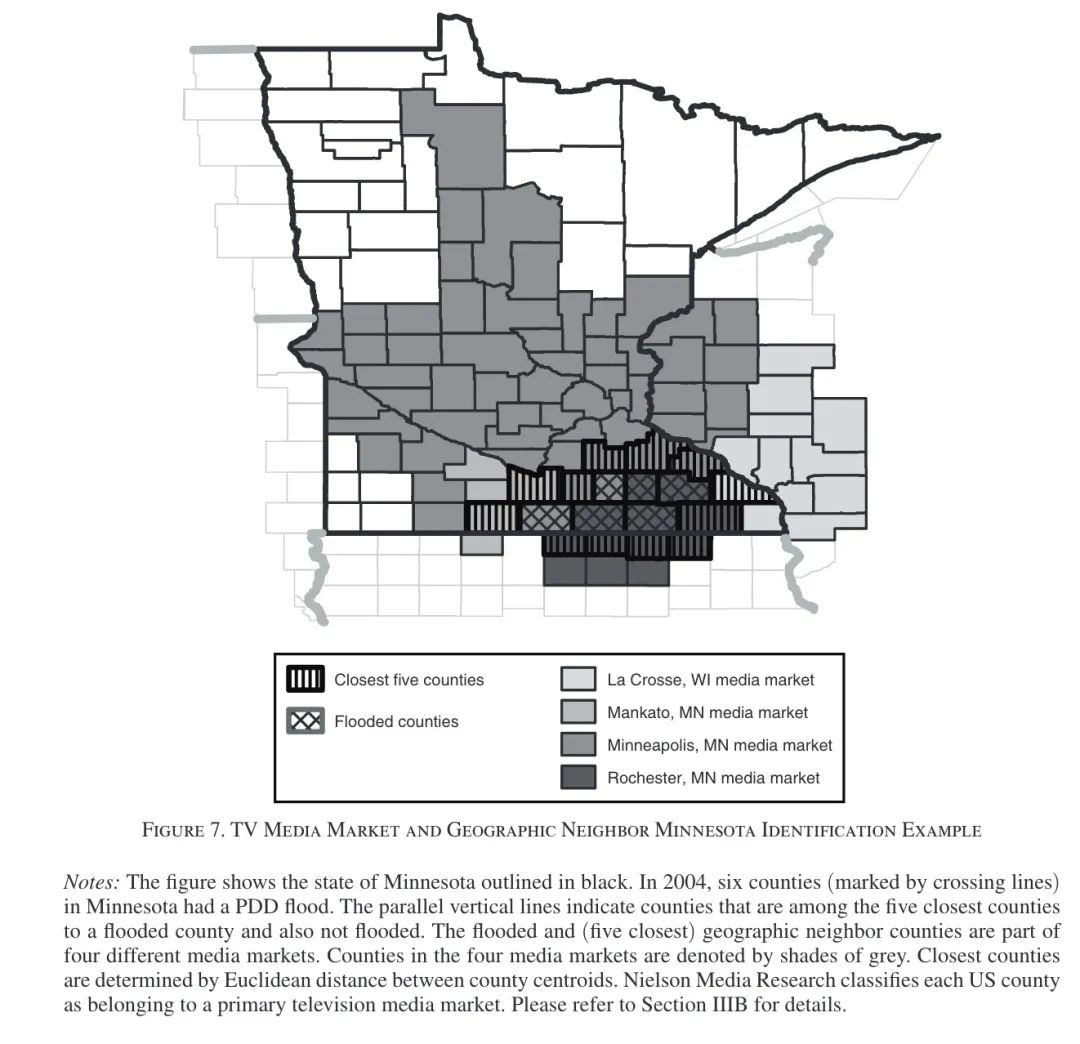
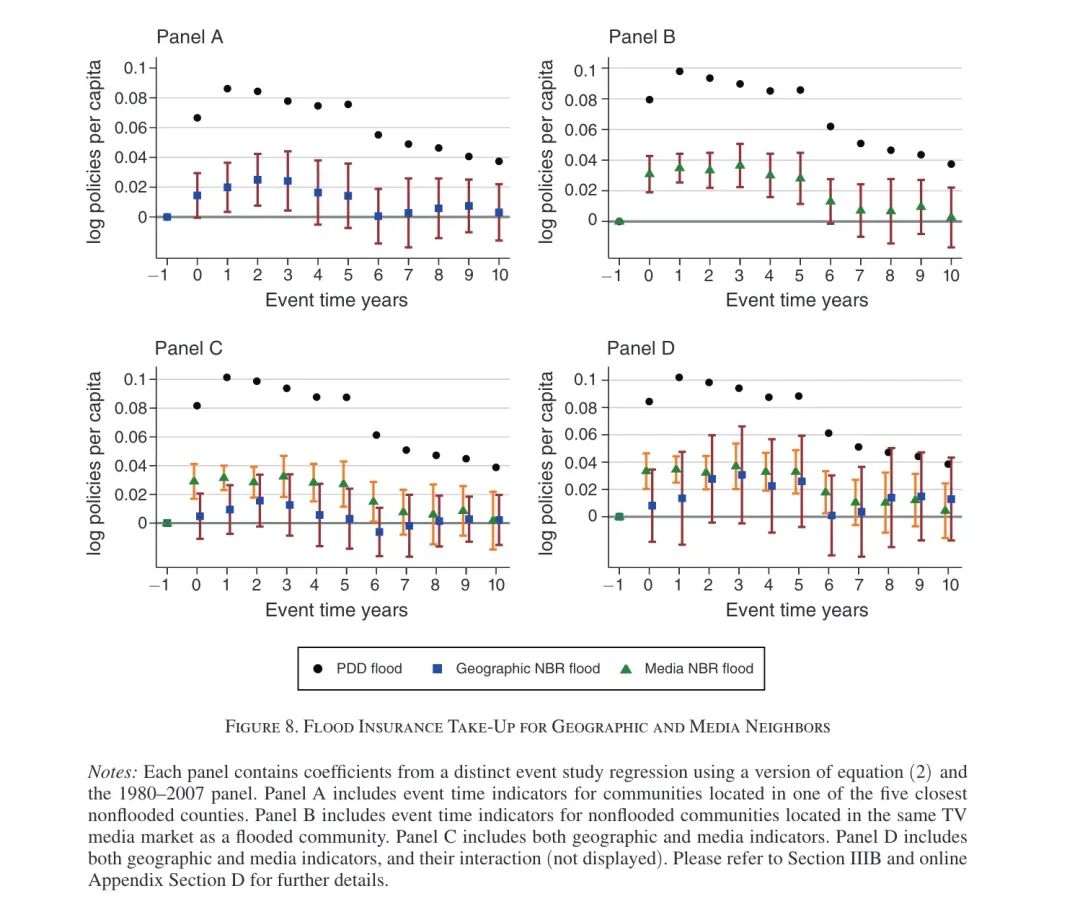
此节使用两种方式度量临近社区，地理距离和共享媒体。地理距离上：将地理相邻社区的定义分为相邻的(未发生洪水)PDD县，或最近的1、5、10或20个(未发生洪水)县。为了便于说明，本文将重点放在最近的五个县的社区上。共享媒体：媒体市场临近是指非洪水社区与洪水社区共享相同的电视媒体市场，地方新闻节目因媒体市场而异。Figure 7中对临近社区的定义进行了说明。事件分析结果见Figure 8中的面板A-D。

Panel A中描绘了地理距离上临近社区洪水灾害对本社区未发生洪水社区的家庭购买保险行为的影响的系数，发现在洪水灾害后的3年事件内显著为正，第4年后不再显著。Panel B中描绘了相同媒体市场中的结果，发现在洪水灾害后的5年时间内显著为正，第6年后不再显著。Panel C中将两种设定同时放入回归中，发现媒体效应基本不变，地理邻居效应基本消失。Panel D中进一步选择了共享媒体市场但在地理上不接近洪水灾害的社区的和地理上接近洪水的社区但不共享媒体市场的样本，这一结果与Panel C相似。这一结果表明，家庭购买保险的决定不受到地理临近社区是否发生洪水的影响，而主要受到同一媒体市场内的社区是否发生洪水的影响。

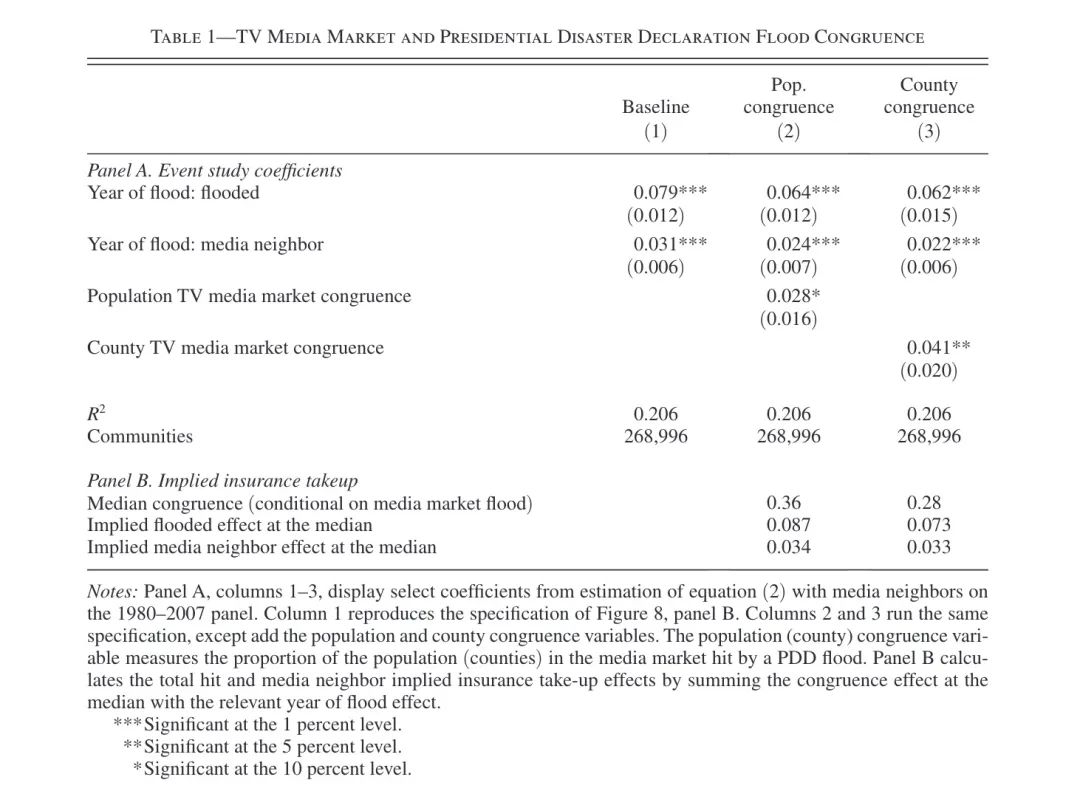
此外，本文也同样估计了媒体市场规模是否会对结果产生影响，Table 1中展示了相关结果。Table 1中的panel A展示了公式（2）和1980-2007年的数据进行回归的结果，第一列为Figure 8 Panel B设定下的结果；第二列和第三列分别加入了两种变量度量媒体市场规模，结果表明在发生洪水后，媒体市场规模会显著促进本地社区购买保险。

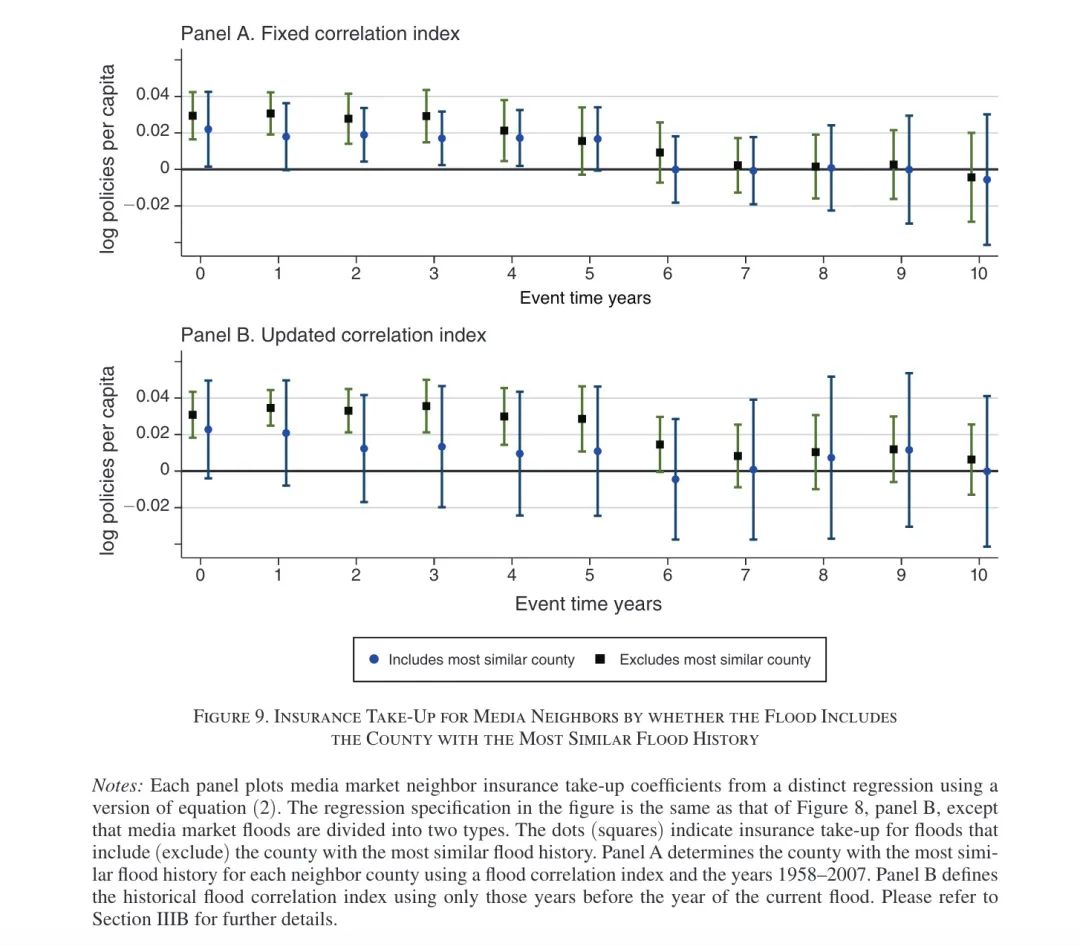
解释：家庭会根据临近社区的洪水信息来评估自身的洪水风险。首先，新的洪水灾害会改变家庭对洪水风险的认知；其次，临近社区的洪水对居住在具有相似洪水特征或洪水历史的社区的居民来说具有不同的重要性。然后，有两项证据表明了家庭并不会因为临近地区的洪水而更新自己的风险认知。首先，Figure 8中Panel C和D均表明地理临近的非洪水地区没有发现在临近社区发生洪水后在保险购买行为上发生显著的差异；其次，Figure 9检验了如果一个发生洪水的社区有类似的洪水历史，那么未发生洪水的社区的家庭是否会在洪水发生后以更高的费率投保。

讨论
 

04

灾难发生后，信念的变化可能与常见的贝叶斯学习模型相一致。假定每个社区的年洪水抽取量独立于一个参数为p的平稳洪水分布。假定某一年发生洪水的概率p分布为Beta(α, β)，那么每个家庭每年洪水发生的条件期望为：

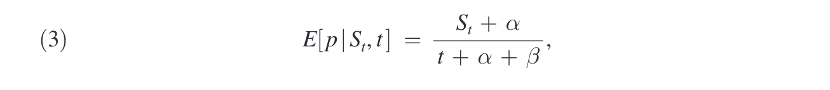
其中，t为年观测次数，St=Σs=1^t ys为观测到的洪水发生次数，α和β为固定参数，表示对洪水的初始信念。上式意味着，随着信息存量的增加，新观测到的洪水对个人信念所产生的影响将变的越来越小。

洪水过后保险费率的大幅飙升，加上这种效应的衰减相对较快，表明家庭可能没有考虑到过去所有的洪水信息。由于家庭没有观测到较早期的洪水灾害或者遗忘，因此可以考虑对每期数据赋予权重，构建模型如下：

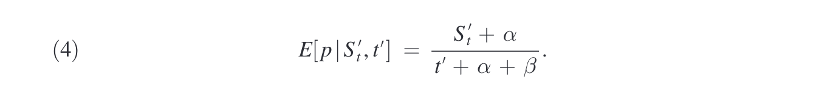
其中，St'表示加权的观测到的洪水次数；t'表示观测期数。

05 

结论

本文利用美国大型区域性洪水和洪水保险的最新面板数据集，为个人如何更新他们对不确定和罕见风险的信念提供了新的证据。研究发现，洪水发生后，洪水保险的购买立即激增，然后稳步下降到基线水平。人口迁移或许能够解释这一现象，家庭在到达一个社区之前可能不知道该地原来发生过洪水，经历过洪水的家庭对最近的洪水将产生不同的信念。

原文链接：https://www.aeaweb.org/articles?id=10.1257/app.6.3.206

 Abstract 

I examine the learning process that economic agents use to update their expectation of an uncertain and infrequently observed event. I use a new nation-wide panel dataset of large regional floods and flood insurance policies to show that insurance take-up spikes the year after a flood and then steadily declines to baseline. Residents in nonflooded communities in the same television media market increase take-up at one-third the rate of flooded communities. I find that insurance take-up is most consistent with a Bayesian learning model that allows for forgetting or incomplete information about past floods.

声明：推文仅代表文章原作者观点，以及推文作者的评论观点，并不代表香樟经济学术圈公众号平台的观点。