
图片来源:百度图片
原文信息:
Acemoglu, D., & Restrepo, P. (2020). Robots and jobs: Evidence from US labor markets. Journal of Political Economy, 128(6), 2188-2244.
一、导论
1929年,约翰·梅纳德·凯恩斯(John Maynard Keynes)曾断言,自动化技术的迅速普及将带来“技术失业”。瓦西里·里昂惕夫(Wassily Leontief)预言 “劳动力将变得越来越不重要……越来越多的工人将被机器所取代。尽管这些预测尚未实现,但人们仍忧心机器人和人工智能的进步将导致大量失业(Brynjolfsson和McAfee,2014;Ford,2015)。越来越多的证据表明,一系列中低技能职业的自动化导致了工资不平等和就业两极分化(Autor、Levy和Murnane,2003;Goos和Manning,2007;Michaels、Natraj和Van Reenen,2014)。尽管存在这些担忧,但对于自动化技术,尤其是机器人对就业和工资的均衡影响,学术界尚未有系统的证据。本文以一种领先型自动化技术—工业机器人—为例,考察其对美国劳动力市场的均衡影响。据统计,机器人技术在20世纪90年代和21世纪取得了显著进步,导致1993年至2007年间美国和西欧(工业)机器人的库存增长了四倍。如图1所示,这个阶段中,美国每千名工人平均净新配备了一台机器人,西欧每千名工人则新增了1.6台机器人。
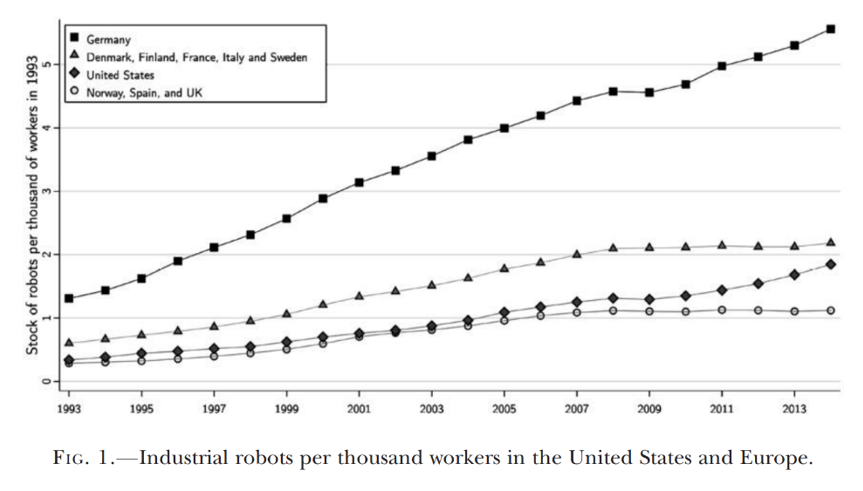
文章提出一个理论模型,刻画了机器人和工人在不同生产任务(task)中的竞争。该模型允许由机器人胜任的任务量份额在不同行业间存在差异,并允许专业化生产不同产品的劳动力市场之间存在着跨地域贸易。理论框架阐明,由于替代效应的存在,机器人对劳动力需求的影响可能与资本深化或要素偏向性的技术进步所造成的影响截然不同。模型进一步表明,机器人对就业和工资的影响效应可以通过将这些变量回归在机器人渗透率上来进行估计。本文根据本地劳动力市场中的各行业的基准就业份额与行业层面机器人采用的技术可能性的交互项来构建机器人渗透率指标(Bartik/Shift-Share)。
实证上,文章以美国的通勤区为研究对象,利用IFR所披露的19个行业(除制造业以外的两位数行业和制造业内的三位数行业)机器人使用量增长的数据以及机器人技术的广泛应用之前的通勤区各行业的就业份额数据,构建起通勤区层面的机器人渗透率指标,以研究机器人渗透对地区就业和工资的影响。文章的识别假设是,相较于机器人技术较慢的行业,通勤区中那些机器人技术进步较快的行业不会受到其他劳动力市场冲击或趋势的差异化影响。基于这一识别策略,文章揭示出通勤区机器人渗透率与1990年后工资和就业水平之间的负相关关系。文章估计表明,1990年至2007年期间,机器人库存的增加(1993年至2007年,每千名工人大约增加一个机器人)使通勤区的平均就业人口比降低了0.39个百分点,平均工资降低了0.77%(相对于没有采用机器人的通勤区而言)。这一结果还暗示了,通勤区额外多安装一个机器人会减少约6名工人的就业岗位。
二、理论模型
2.1 模型概述
该理论模型是基于一个机器人和工人在不同任务的生产中进行竞争的模型。模型证明了,机器人技术的进步会对工资和就业产生负面的替代效应(因为机器人直接取代工人从事他们以前执行的工作),但也有积极的生产效应(因为其他行业和任务增加了他们对劳动力的需求)。
模型推导依次分为两部分:一是通勤区之间不存在贸易时的机器人影响;二是通勤区之间存在贸易时的机器人影响。
2.2 通勤区之间不存在贸易时机器人的影响
整个经济体由多个通勤区c组成,一个通勤区的总产出Yc由各个行业i的产出Yci按比例vi加权组成,σ>0代表不同行业生产的商品之间的替代弹性。
通勤区的总产出为:
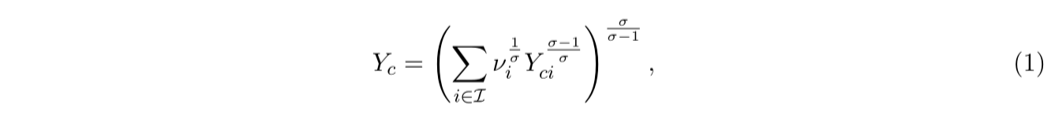
在均衡中,通勤区内每个行业的产出量等于消费量,Yci=Xci;消费品的价格为Pcix。
每个行业的产出由资本Kci和一系列连续的任务s∈[0,1]结合生产而成,xci(s)表示生产消费品Xci时的任务数量,每一个任务都能由机器人或者工人来完成。
通勤区c中i行业产出的消费品数量为:
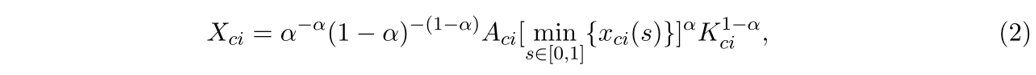
其中,Kci表示非机器人资本,1-α代表在生产要素中的比例,Aci代表该行业的生产率,生产任务数量xci(s)在机器人和工人之间的分配方式为:
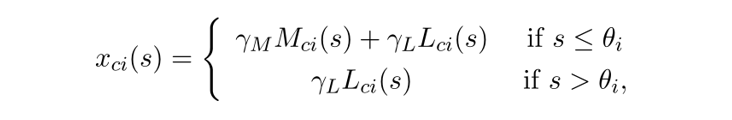
其中,γL和γM分别表示工人和机器人的生产率,均大于0;Lci(s)和Mci(s)分别表示在任务s中使用的工人数量和机器人数量;[0,θi]表示能够使用机器人进行自动化生产的限度,随着时间的演进,越来越多的任务被自动化。
在一个通勤区c中,由家庭提供的劳动力(工人)供给数量满足以下家庭效用函数:
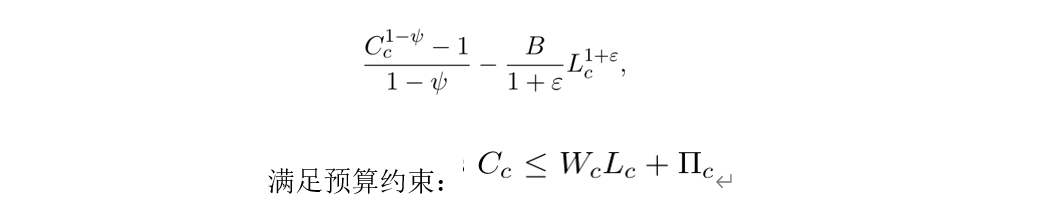
其中,Cc代表家庭的消费量,Lc代表劳动力供给量,ψ代表劳动力供给的收入弹性,ε代表劳动力供给的工资弹性的倒数。该效用函数需满足以下约束条件,其中,Wc代表每个工人的价格,Πc表示该家庭的非劳动收入。
机器人本身需要用最终商品来投资生产,每个通勤区的投资数量用Ic表示,机器人的数量为:
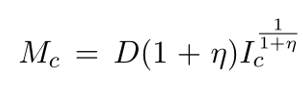
其中,η>0使机器人数量随着投资的增加而呈现出边际产量递减的特征。另设机器人的租金为RcM;通勤区C内固定供应的资本Kc的价格为RcK。
于是,一个通勤区内的均衡结果由均衡价格{Wc, RcM, RcK}c∈C(劳动力价格、机器人价格、资本价格)和均衡数量{Cc, Yc, Ic, Lc, Mc }c∈C(家庭消费数量、总产出数量、投资数量、劳动力数量、机器人数量)共同决定。
上述均衡结果由企业利润最大化、家庭效用最大化以及 劳动力、机器人、资本和最终商品市场出清条件所导出
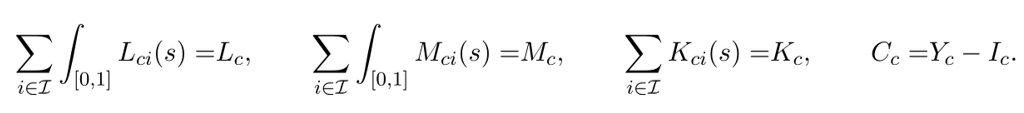
为专门分析均衡状态下来自于机器人的影响,本文首先定义了通勤区中使用机器人所节省的成本为:
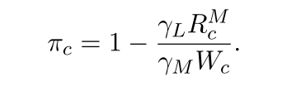
当πc <0时,企业不会使用机器人;当πc >0时,则有
命题1:
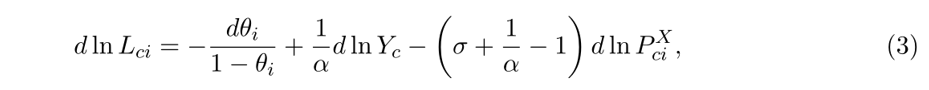
其中,dθi表示机器人技术进步对各个行业劳动力需求的局部均衡影响。
方程式(3)强调了影响i产业劳动力需求(以Lci来衡量)的三种不同力量。
替代效应:机器人应用于原本由劳动力执行的任务,取代雇佣工人。
补偿效应:自动化行业以牺牲其他行业为代价进行扩张,这提高了对非自动化任务劳动力的需求。
生产率效应:自动化降低了生产成本,提高了所有行业非自动化任务的劳动力需求。
将命题1拓展为对整个通勤区劳动力需求的影响,可得:
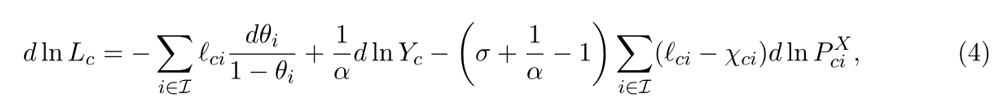
其中,lci表示行业i在通勤区c的总就业中所占的比例;χci表示该行业在当地经济附加值中所占的份额。
式(4)中的前两项与式(3)中的替代效应和生产率效应相类似。第三项表明,劳动力需求的构成效应的影响取决于自动化(机器人的推广过程)是否正在将产出重新分配给劳动密集度高于平均水平的部门(即lci>χci的部门)。当所有行业都拥有相同的劳动力份额时,这种效应就会消失。
等式(4)刻画了自动化后劳动力需求变化的局部均衡特征。下一个命题将价格P和总产出Y的变化与自动化技术联系起来,从而得出自动化所导致的一般均衡效应。
命题2:假设在所有通勤区c中πc>0,在所有行业i中θi=0,则有:
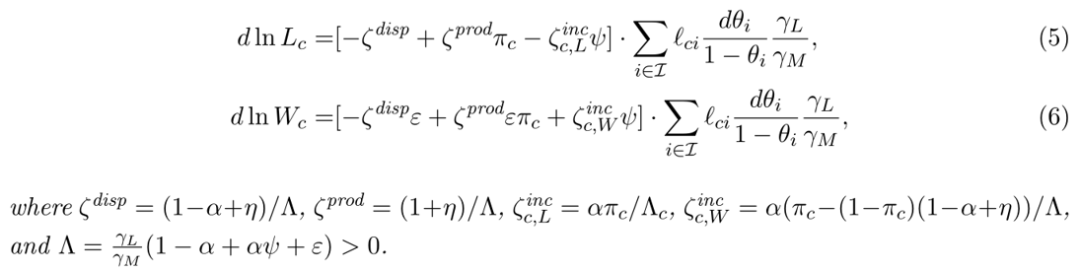
命题2表明就业和工资对自动化的响应是由
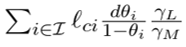
这一项所决定,这成为文章后续以机器人渗透率(exposure to robots)作为测度指标的基础。此外,两个方程中该变量的系数包括三个项:第一项,-ζdisp表示机器人对劳动力的替代效应;第二项,ζprod表示机器人节约生产成本πc所带来的生产率效应,当自动化带来的成本节约有限时,自动化就会减少就业和工资,相反,当πc较大时,自动化将会产生正面效应;最后,两个方程中的第三项ζinc都包含了自动化对劳动力供给的负收入效应。
根据命题2可以看出,机器人的影响与总体资本深化(资本供给Kc的增加)、机器人生产力的技术变革γM、行业生产力Aci所产生的影响是显著不同的。资本深化、机器人生产率的提高和工业生产率的提高并不会取代正在执行任务的工人的工作,而只是提高了工资和就业率。这一观察使得自动化产生的替代效应:劳动力需求的潜在负面影响变得更加清晰。
2.3 通勤区之间存在贸易时机器人的影响
文章接下来将基准模型推广至开放经济环境中,模型设定增加了如下新的元素:
首先,假设家庭效用取决于可贸易的商品Cc和不可贸易商品Sc(例如服务业),φ∈(0,1)表示家庭支出花费在可贸易商品中的比例。家庭效用变为:
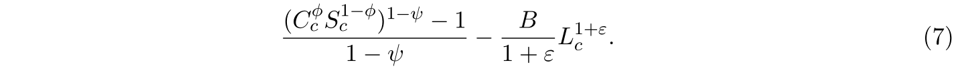
假设不可贸易商品由劳动力生产,Sc=LcS,不可贸易商品在通勤区c中的价格为Pc,那么剩下来用于生产可贸易商品的劳动力为Lc-LcS。
然后,假设所有要素投入来自于所有通勤区,则通勤区c中行业i的产出为:
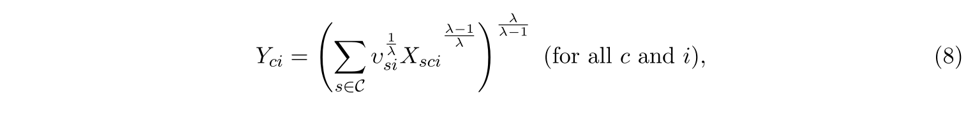
其中,λ表示不同通勤区之间的替代弹性,vsi表示不同来源的比例。
假设不存在交易成本,因此可交易商品的价格在通勤区之间是相等的, 从通勤区c出口至目的地d的商品i的数量为:
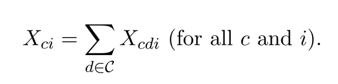
此外,还假设初始资本存量K可以在通勤区之间自由流动;家庭效用的约束条件改为:
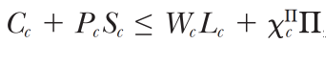
其中,Π是全国非劳动收入,XcΠ是通勤区c在全国非劳动收入中的占比。
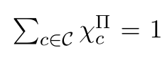
与命题2相似,文章提出命题3:假设所有通勤区中πc=π0且所有行业中θi=0,则有:
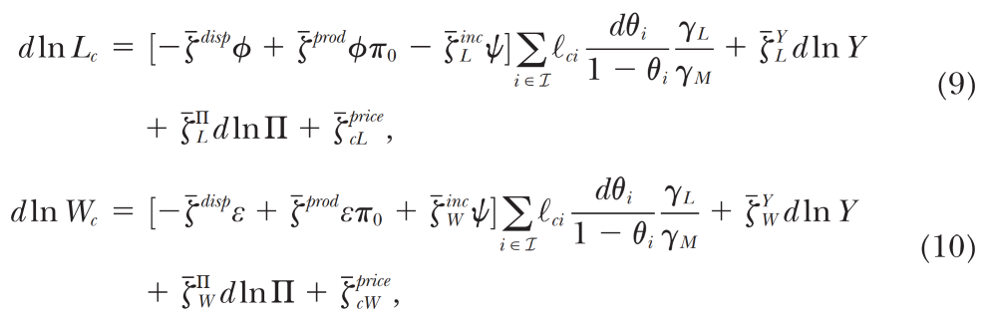
与基准模型一样,“ζ”总结了机器人对当地就业和工资的影响。通勤区之间的贸易意味着,一个地区的生产力提高和价格变化将与其他地区共享。由于国民收入的变化dlnY、非全国性劳动收入变化dlnΠ和价格变化ζprice均不是机器人渗透率的函数,由此,本文得到了与封闭模型中类似的机器人与本地劳动力需求之间的约简式关系(reduced-form relationship)。也成为后文计量模型设定的基础。
三、计量模型构建与指标选取
根据命题二和命题三的相应结论,可以相应写出外生的机器人技术进步与本地劳动力需求及工资之间的约简式(reduced-form)关系:
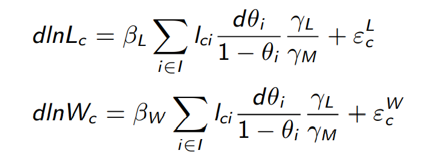
直观来看,我们可以利用观测性数据构造核心解释变量“通勤区c中的机器人渗透率”:

其中,lci是行业i在通勤区c的劳动力就业份额;APRi是美国行业i中的机器人利用状况,其具体形式为:
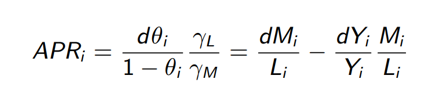
根据约简式关系,本文的计量模型可以被设定为如下形式:

然而,上述计量模型将面临两个潜在的内生性威胁:(1)行业机器人采用的选择性;(2)影响地区c劳动力需求的其他冲击。
为解决上述问题,作者所给出的解决思路是:寻找由外生技术改进而驱动的机器人渗透率变化。即文章实际使用的行业层面机器人渗透率是欧洲五国从t0期至t1期的行业机器人采用的变化:
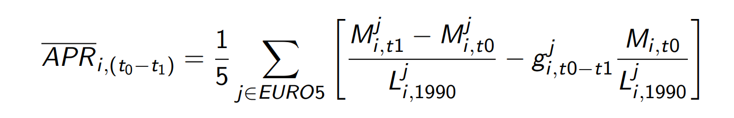
在长差分模型中,欧洲的t0设为1993年,t1设为2007年。
由于文章实际使用的个体观测单位为通勤区(Commuting Zone),因此还有必要基于行业层面的机器人渗透率来构造通勤区层面机器人渗透率指标。

地区层面机器人渗透率采用Shift-Share类型的构建方式:即结合了机器人使用的行业层面变化和基准就业份额。值得指出的是,本文之所以使用欧洲行业层面的机器人渗透率作为shift,是因为欧洲国家在机器人技术上领先美国,有助于保证机器人对就业的影响来源于外部力量驱动的技术进步,而不是来自于美国的特殊因素(这些经济体之所以领先于美国,部分原因是他们的人口轨迹产生了对机器人更大的需求;见Acemoglu和Restrepo,2018)。
四、行业相关性事实
在进行实证分析之前,文章提供了四个层面的行业相关性事实。
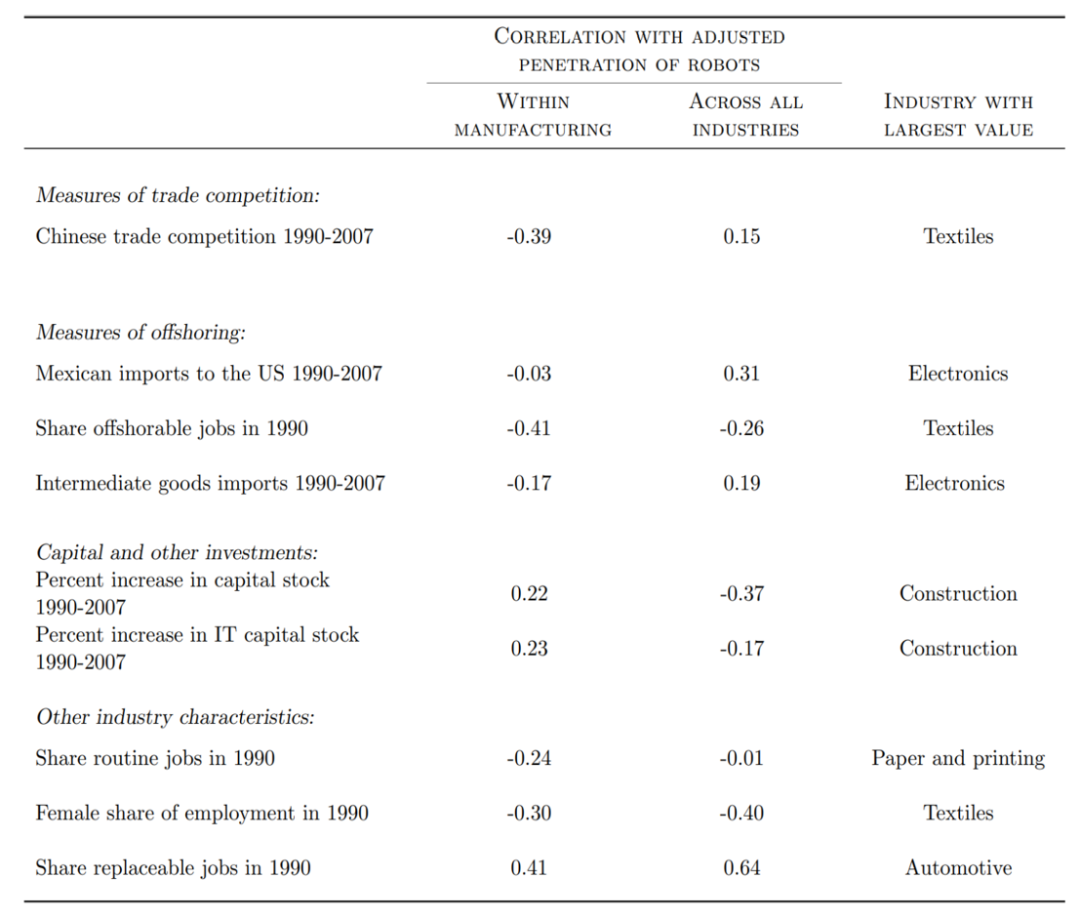
行业层面的相关性事实之一:行业机器人渗透率越高,工人工资越低,工人就业人数越少,该行业的附加值越高,行业劳动力份额越低。
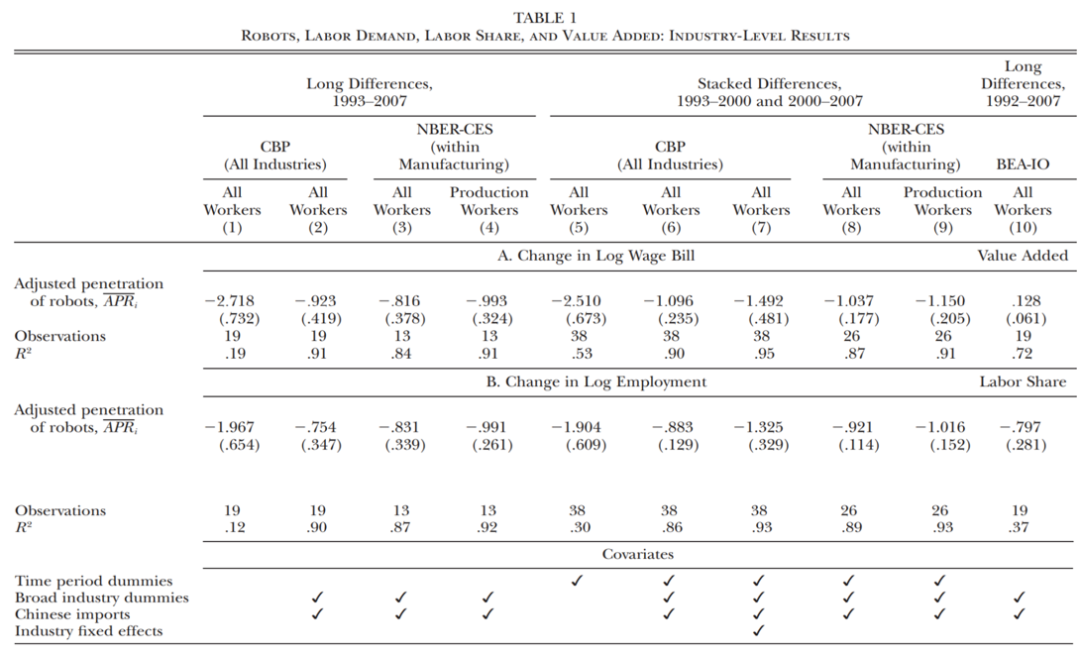
行业层面的相关性事实之二: 基于表1第8列所得到的残差图,可以直观看出行业机器人渗透率(1993-2007年)和间行业工资(1993-2007年)和行业就业(1993-2007年)之间存在负相关关系。
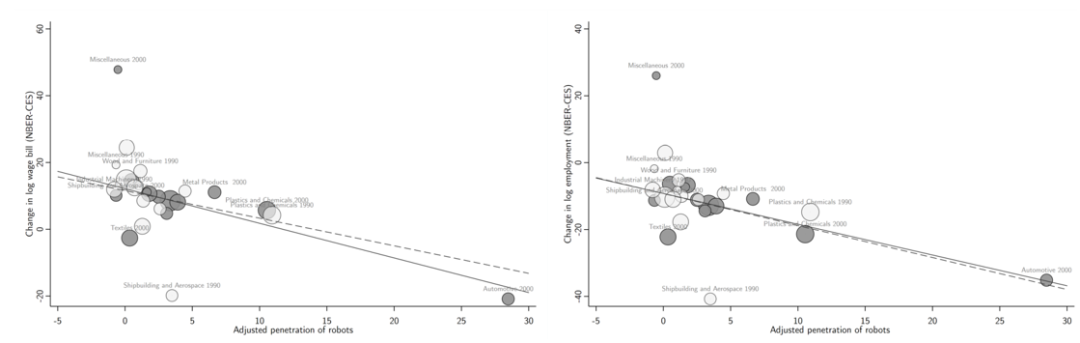
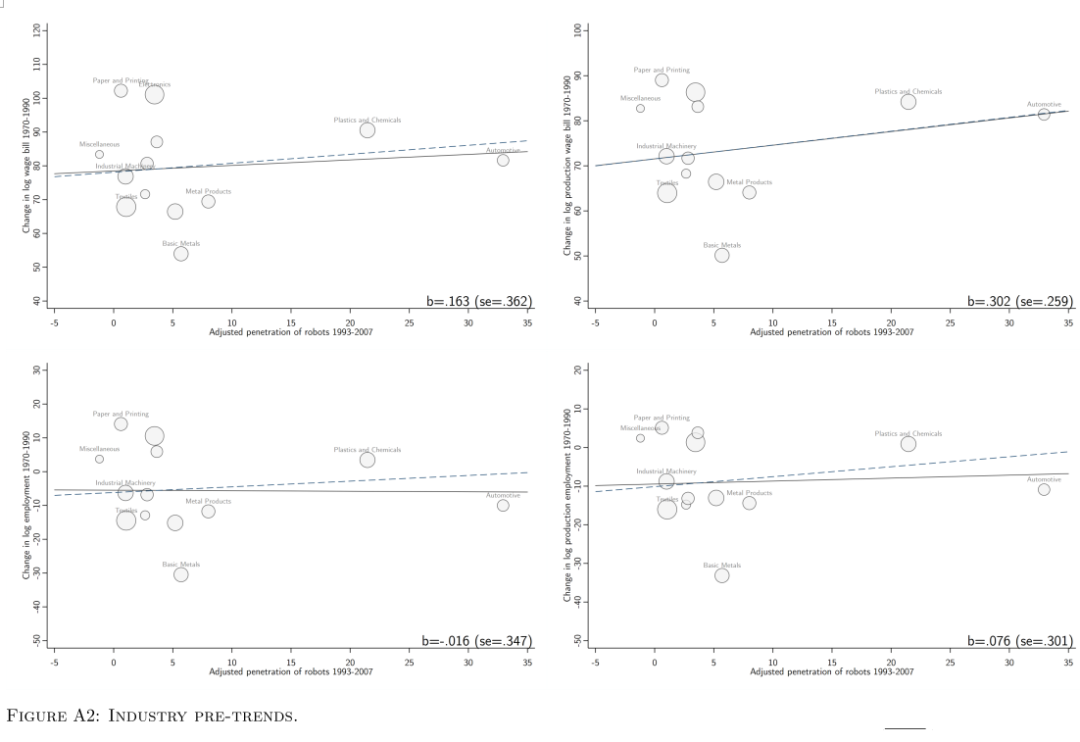
行业层面的相关性事实之三:行业机器人渗透率(1993-2007年)与工资和就业(1970年-1990年)间无显著关联(排除事前趋势)。
行业层面的相关性事实之四:行业机器人渗透与行业层面的中国、墨西哥进口量、资本存量、IT资本增长、 任务可离岸化和中间产品离岸化等均无显著关联(排除混淆因素)。
五、通勤区层面的回归结果
5.1 基准回归结果:
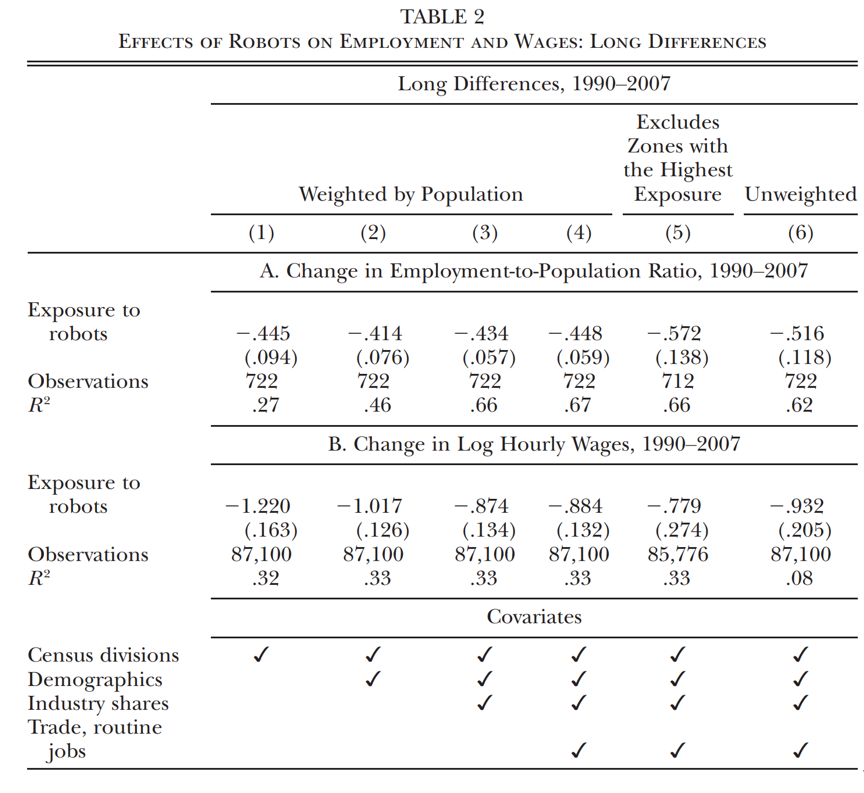
表2给出了1990-2007年长差分模型的估计结果,其中作者将1990年至2007年期间就业和工资的变化回归在相同阶段中的机器人渗透率上。作者以2007年为样本结束年,以避免大衰退可能带来的混淆效应,并在附录中展示了更长时间窗口以及更近时期的结果。表2侧重于主要结果变量:Panel A中的(私人)就业占总人口比率和Panel B中的小时工资对数值。其中基准结果按1990年的人口进行加权,并在括号中报告了异方差性和具有空间相关性的稳健标准差。
第1列只包括人口普查部门的虚拟变量作为协变量。在Panel A中,我们发现在通勤区机器人渗透与就业变化之间存在强烈的负相关关系,系数为-0.44(标准误=0.09)。这一估计表明,接触机器人的工人每千人中每增加一个机器人,(私人)就业人口比相对下降0.44个百分点。第2列控制了1990年的人口特征,特别是人口的对数值;女性在人口中的比例;65岁以上人口比例;无学历的人口比例;以及白人、黑人、西班牙裔和亚洲人在人口中的比例。第3列控制了制造业和轻型制造业的初始就业份额以及女性在制造业中的就业份额。第4列控制了在本文分析期间影响劳动力市场结果的其他变化:1990年至2007年间从中国的进口以及常规职业的下降(由常规职业的基准就业份额衡量)。第5列在第4列的模型设定的基础上,剔除了机器人渗透率最高的通勤区的前1%样本,并证明这些高机器人渗透率的通勤区并不是估计值为负的主要原因。Panel A中的系数估计值增加到-0.57(标准误=0.14)。
Panel B显示了以对数小时工资为因变量的结果。具体而言,作者使用1990年至2007年间通勤区250个人口单元中每个单元的平均工资变化作为因变量。并根据1990年通勤区人口规模对每个观察值进行加权。估计显示,更高的机器人渗透会降低工资。第4列的系数估计值为-0.88(标准误=0.13)。这意味着机器人渗透率每增加一个机器人(每千名工人)会导致小时工资降低0.87%。
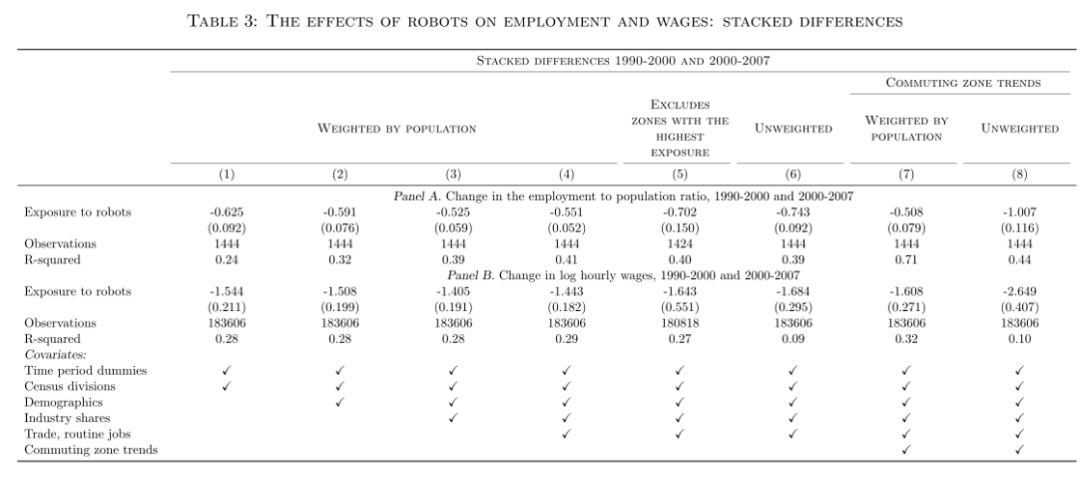
接下来,作者还提供了堆叠差分模型的估计结果(见表3),作者采用的是1990-2000年和2000-2007年的两期面板数据。表3的PanelA关注就业,Panel B关注小时工资。前六列的结构与表2相同。整体可以发现,在这两个Panel中,估计值都比以前负得更多。堆叠差分模型利用了与长差分方法不同的变异性来源,(长差分模型的变异性来源:1990-2007年间,不同通勤区机器人渗透率的变化程度差异;堆叠差分模型的变异性来源:1990-2000和2000-2007两个阶段之间,不同通勤区机器人渗透率的变化差异)。实证结果显示:机器人渗透对就业和工资都会产生显著的负面影响。这些发现表明,通勤区机器人渗透的提高并不仅仅来自于和机器人技术进步无关的差异化趋势上。
5.2 稳健性检验
5.2.1 前期趋势的干扰
本文识别假设存在着两个主要威胁:首先,由于需求下降、国际竞争、其他技术变革或劳资关系恶化,过去二十年(美国和欧洲)采用更多机器人的行业可能呈下降趋势。其次,采用更多机器人的行业所在的通勤区可能会受到其他负面冲击的影响。无论是哪种情况,我们的估计都可能混淆机器人的影响与这些行业和通勤区的事前趋势。作者认为行业层面的相关性事实说明,欧洲五国的机器人渗透与行业的事前趋势或影响劳动力需求变化的其他因素无关,因此第一个威胁是令人放心的。此外,作者发现机器人普及率最高行业的行业增加值是提高的,这排除了行业层面负面需求冲击的影响。对于第二个威胁,作者一方面在堆叠型差分模型中控制通勤区趋势,表明线性的通勤区趋势并不能解释本文的估计结果。更进一步,作者通过检验事前趋势(见表4)来直接讨论这一潜在威胁。
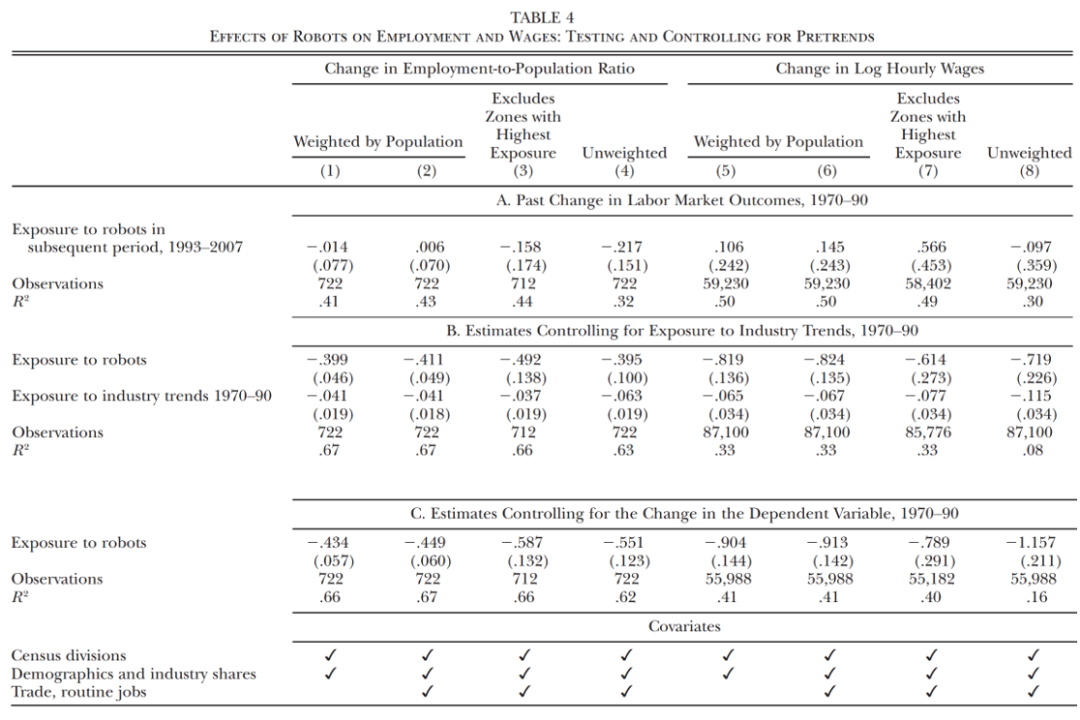
表4Panel A拒绝了事前趋势的存在。1-4列以1970年至1990年间的就业人口比为因变量,5-8列以1970年至1990年间的对数小时工资为因变量。结果表明,机器人渗透与1990年前的就业或工资变化之间没有显著关联。在第3列和第7列中去除掉高渗透率的通勤区,以及在第4列和第8列中报告未加权的估计时,结果是类似的。
表4PanelB研究了可能存在的混淆性的行业趋势。具体而言,作者在回归中控制了预测的行业就业下降趋势。虽然在一些列中,这些行业趋势变量的系数为负且显著,但是核心变量机器人渗透率的估计值不受影响。
表4Panel C则直接控制了1970-1990年间的就业人口比或小时工资的变化。这一控制对实证结果也没有影响。
5.2.2 汽车行业极端值的影响
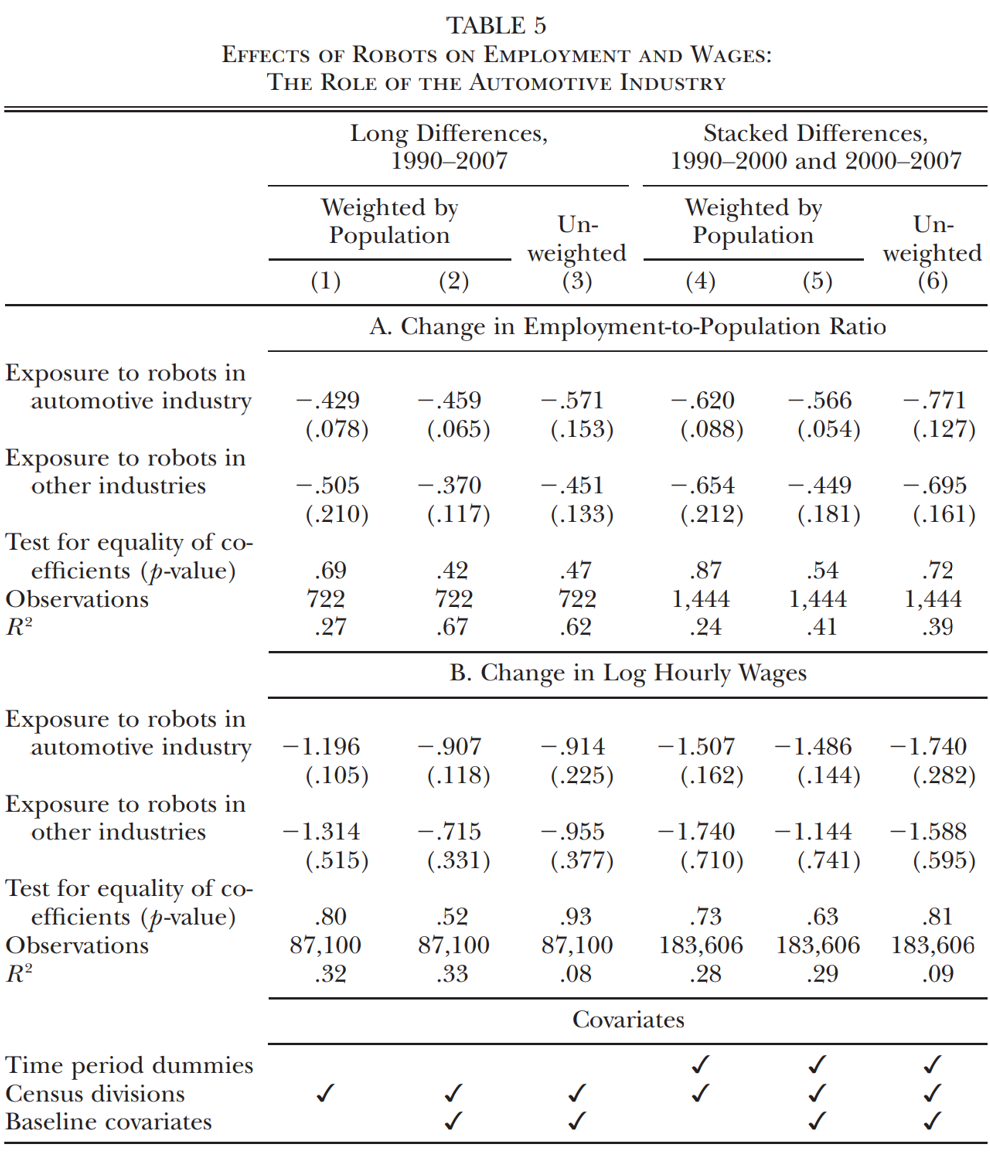
另一个担忧是由于汽车行业在1993年至2007年间采用的机器人数量超过了任何其他行业,因此估计结果可能受到汽车行业极端值的影响。为了解决这一问题,作者在表5中,同时纳入了两个变量;一个是汽车行业的机器人渗透率,另一个是所有其他行业的机器人渗透率。表5列出了长差分模型(第1-3列)和堆叠型差分模型(第4-6列)的结果。Panel A讨论就业,Panel B讨论工资。系数差异检验得出,汽车行业机器人渗透的影响与其他行业机器人渗透的影响是没有显著差异。这表明,主回归结果并非完全由汽车行业所驱动。
5.2.3 资本深化、IT技术、行业自身发展的影响
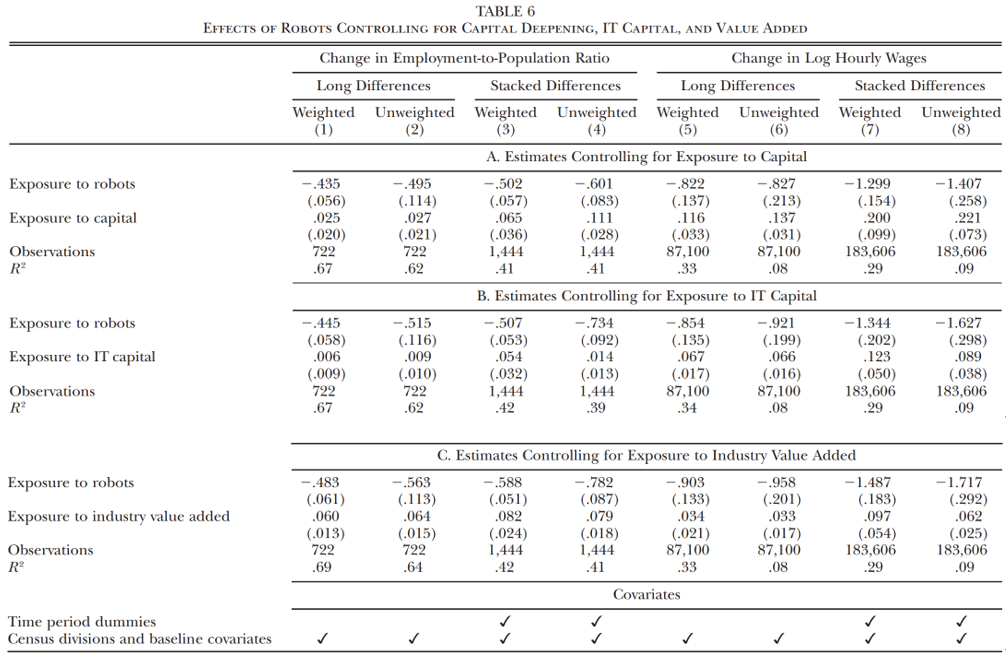
理论模型还表明,资本深化和技术变革不会对劳动力产生替代效应。基于此,作者将检验资本深化、IT资本增加和增加值的增长对就业及工资的影响是否有所不同。
表6展示了长差分和堆叠差分模型的估计结果。前四列讨论就业,后四列讨论工资。在Panel A中,作者控制了资本深化(Bartik指标构建:log(行业资本存量增长)×行业初始的就业份额)。在Panel B和Panel C中,作者相应控制了IT资本(Bartik指标构建:log(行业IT资本存量增长)×行业初始的就业份额)和行业附加值(Bartik指标构建:log(行业增加值增长)×行业初始的就业份额)。结果发现,控制这些变量对机器人的估计系数几乎没有影响,从而证实了本文理论模型所做出的预测。
5.3 异质性检验——行业、职业、性别和技能的影响
接下来,作者研究了机器人渗透如何影响不同行业和职业的就业,以及如何影响不同工人的就业和工资。
5.3.1 行业和职业类型异质性
图8中的Panel A显示了机器人渗透对不同行业就业的影响程度的估计。作者分别给出了基于长差分模型、堆叠型差分模型以及去除极端值后模型设定的点估计值和置信区间。图8显示,机器人的影响集中在制造业,尤其是高度自动化的行业,包括汽车、塑料和化学品、金属制品、基本金属、电子产品以及食品和饮料。对其余的制造业没有明显影响。同时,作者也发现了机器人对建筑、零售和个人服务业等非贸易品部门的负面影响。而农业和教育、卫生保健和公共部门没有表现出显著变化。
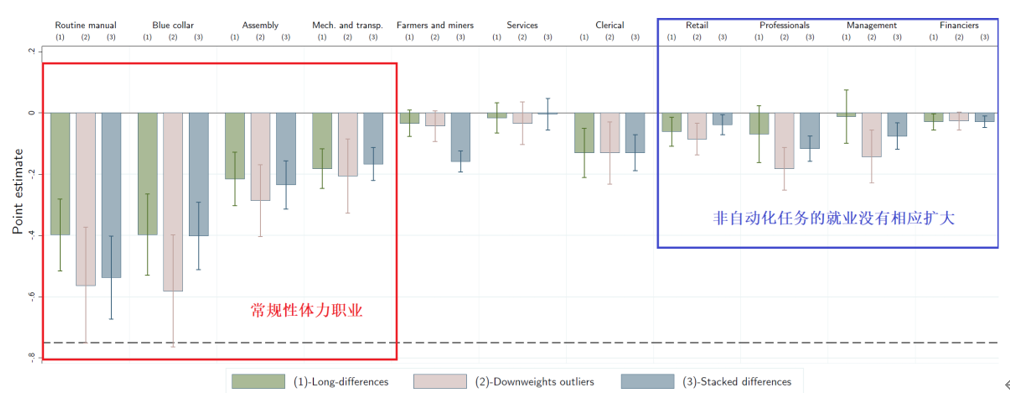
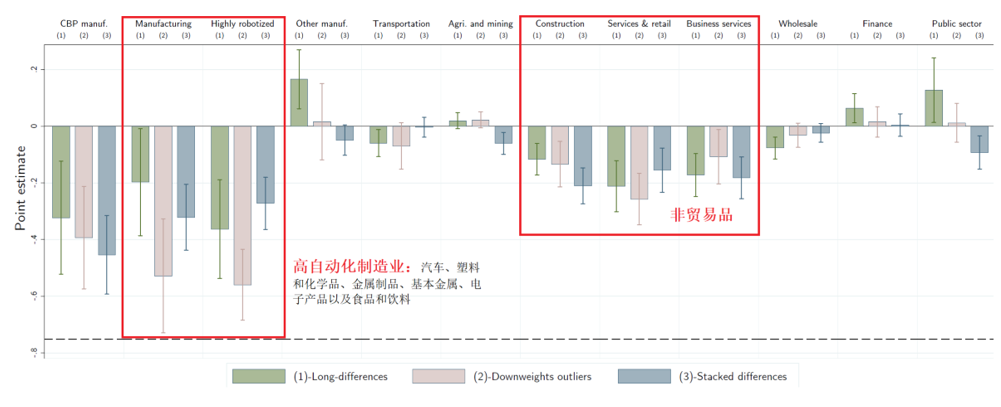 图8中的Panel B显示了按职业划分的就业状况。与预期一致,机器人对就业的负面影响主要表现在常规性体力职业,尤其是蓝领职业,如机械师、装配工、材料处理工和焊工。与此同时,没有证据表明机器人渗透会对其他职业产生的积极就业影响。
图8中的Panel B显示了按职业划分的就业状况。与预期一致,机器人对就业的负面影响主要表现在常规性体力职业,尤其是蓝领职业,如机械师、装配工、材料处理工和焊工。与此同时,没有证据表明机器人渗透会对其他职业产生的积极就业影响。
5.3.2 受教育程度和性别异质性
图9展现了机器人对不同教育群体工人就业和工资的影响。可以看出,机器人对高中以下、高中学历、大学、专业学位以及硕士或博士学位的工人的就业和工资都会产生负面影响(对硕士以上学历人群的影响不显著),且这种影响在男女生中都存在。值得指出的是,机器人渗透对研究生学位的工人就业没有积极影响。
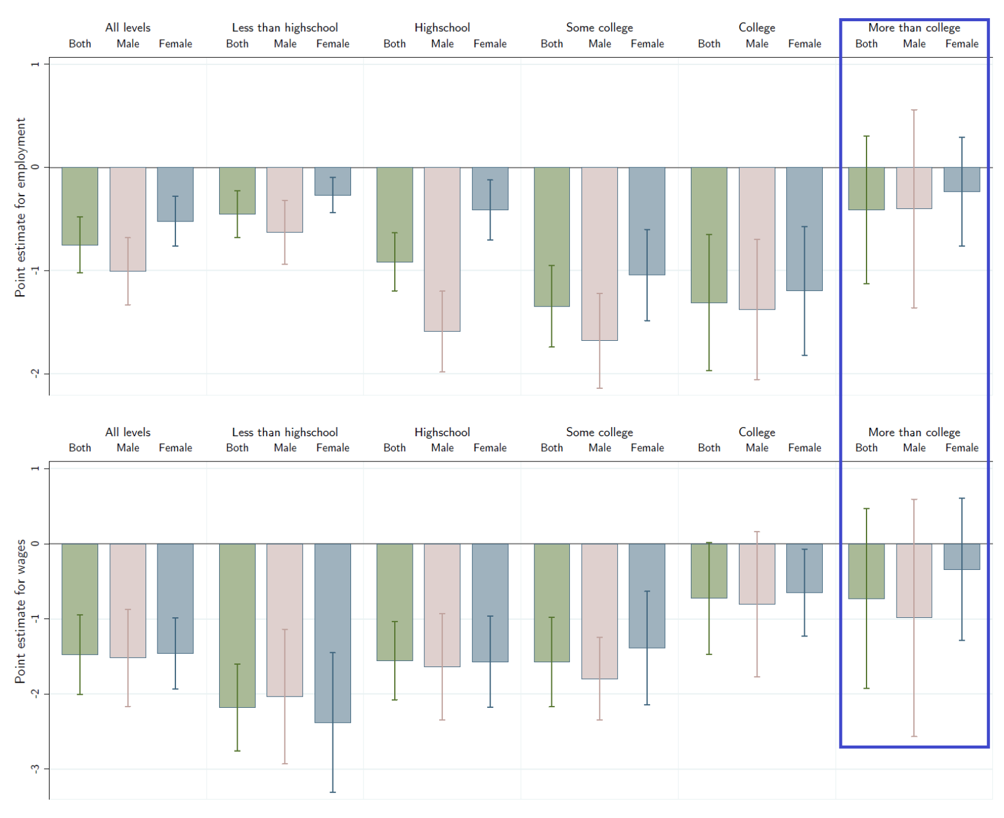
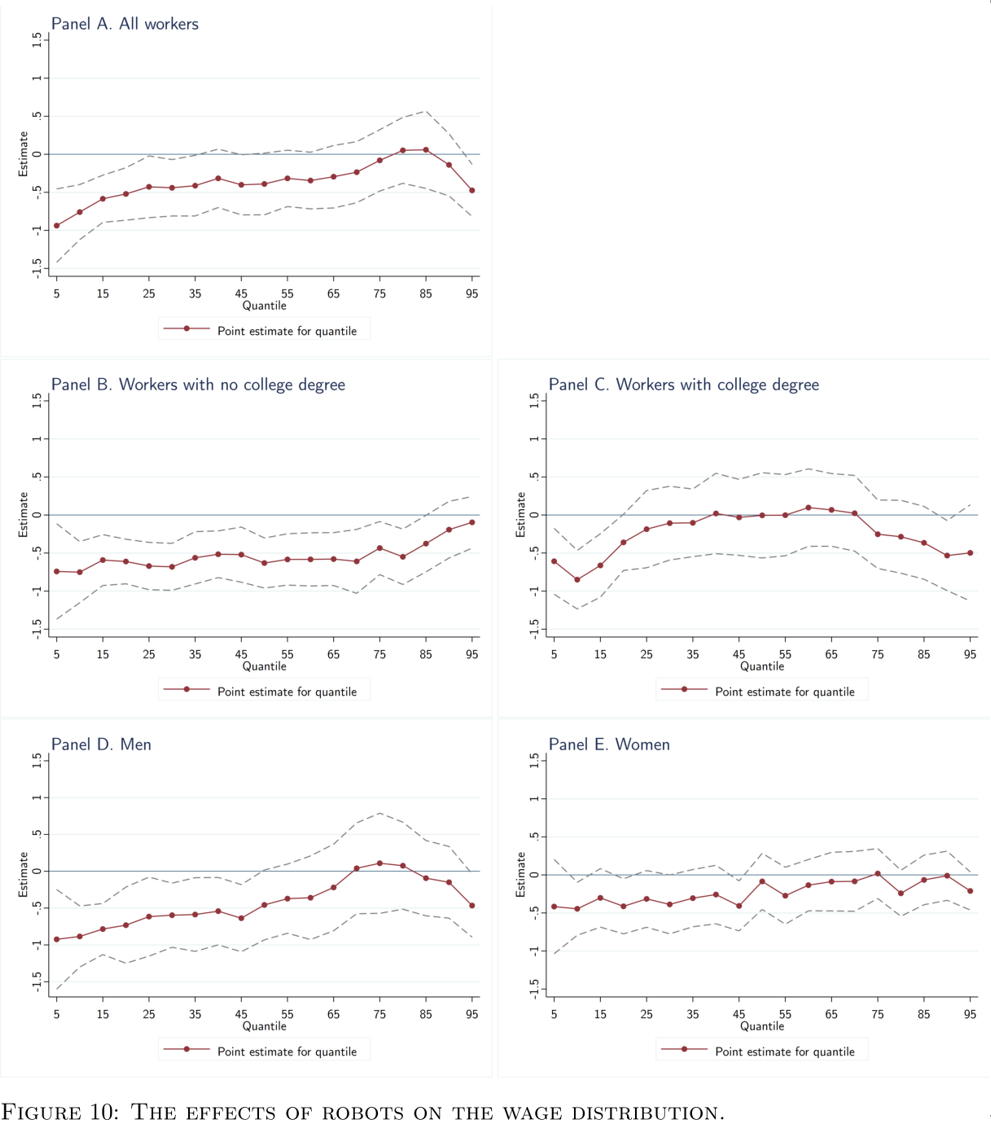
5.3.3 工资分布异质性
图10通过分位数回归研究了机器人渗透对工资分布的影响。结果显示,全样本中,机器人对低收入人群(25%以下)具有显著的负面影响,对高收入人群(75%以上)的影响并不显著。对于没有大学学历的工人而言,这种负面影响将一直延伸到85%分位上;而对于大学以上学历的员工,负面影响则集中在15%分位以下。这表明,机器人渗透对工资的负面影响主要位于分布的底部和中间。
六、工具变量回归
表7中,作者使用工具变量(IV)法来研究机器人渗透的影响。第1-3列的因变量为就业占人口比,第4-6列的因变量为对数小时工资。第一列仅控制了人口普查部门的虚拟变量;第二列额外控制了通勤区的人口特征和行业构成;第三列额外还控制了从中国的进口和常规工作岗位的减少。Panel A的时间跨度为1990-2007年,由于年份所限,仅有的2004-2007年美国行业机器人数据被重新调整为跨度14年的样本。Panel B的时间跨度也为1990-2007年,但利用的是1993年至2004年美国宏观机器人数据来推算美国各行业的机器人利用数据,从而构建了美国的实际行业机器人渗透率指标。Panel C的时间跨度为1990-2014年,Panel D和Panel E则分别考察2000-2007年和2000-2014年。在所有列中,使用2SLS方法对就业和工资的估计都显著为负的。
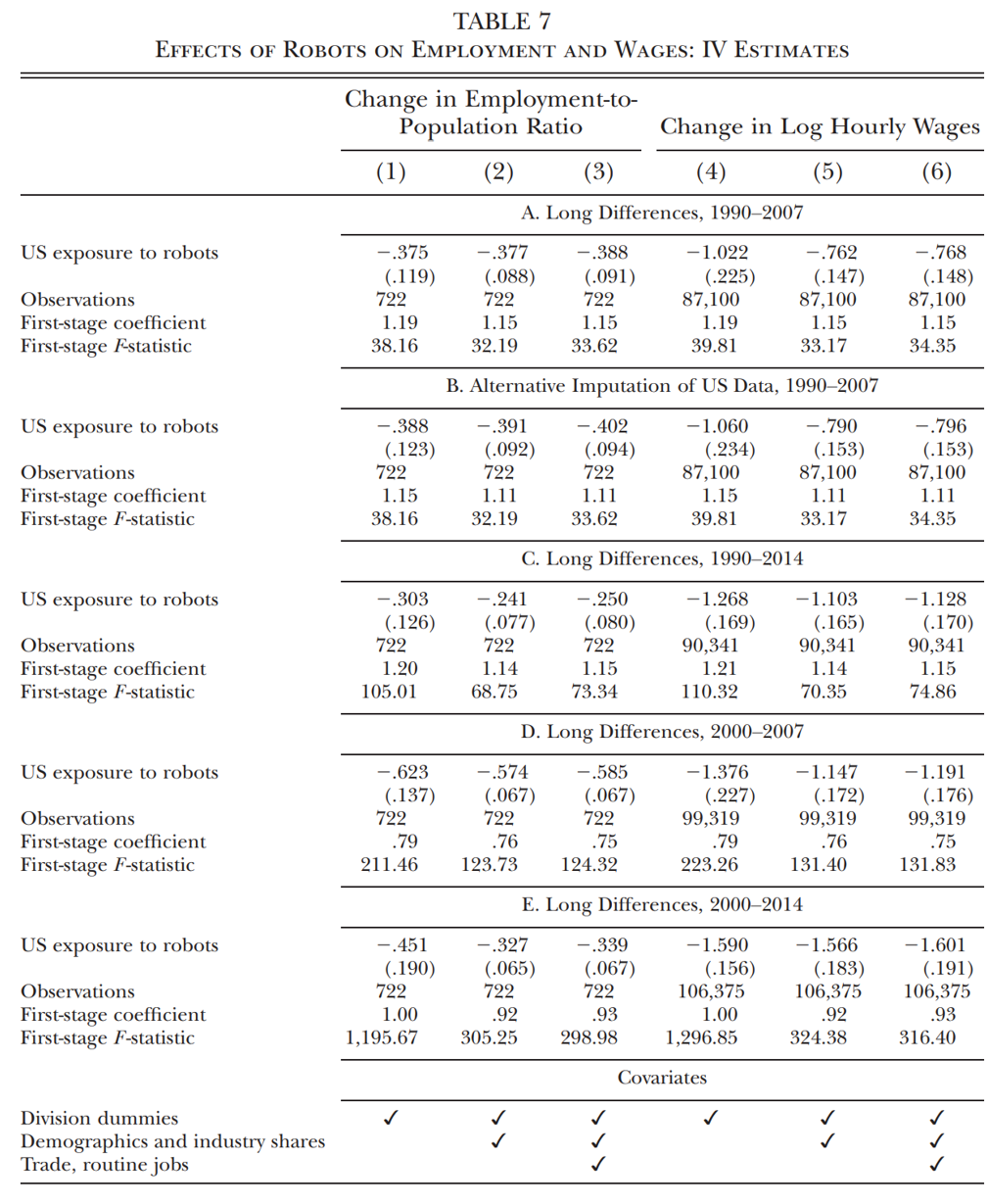
从经济意义显著性来看,工具变量估计(Panel A第3列)表明,每千名工人增加一台机器人导致(私人)就业与人口比率降低0.39个百分点,根据下列换算过程,我们可以进一步推论:额外增加一个机器人将减少约6名工人的就业机会。

为直观反映机器人渗透的影响,作者还援引Autor、Dorn和Hanson(2013)的研究,该文估计得出来自中国的进口将导致美国的就业人口比下降约1个百分点,这一影响大约为机器人影响的2.5倍。
七、结论
本文使用通勤区来近似本地劳动力市场,估计了机器人对就业和工资产生的强劲负面影响。主要发现可以总结为以下三点:
(1)机器人采用与常规工作的普及率、从中国进口、从墨西哥进口、离岸外包、IT资本和资本深化只有弱相关性;
(2)机器人的采用与IT技术和整体资本深化的经济效应截然不同;
(3)每千名工人增加一台机器人,当地就业人口比就会减少0.39%,工资也会减少约0.77%。即使考虑了溢出效应的存在,影响仍有0.2%和0.42%。
本文在以下方面可供学习和借鉴:
1.强化理论模型与约简式回归模型间的契合度:与一般性文献直接给出约简式计量模型的惯常做法不同,本文计量模型严格遵循一般均衡模型系统,经求解得出。这不仅为线性约简式模型的构建提供理论依据;也为进一步的因果关系识别埋下伏笔(理论命题所蕴含的系数作用方向是不确定的,需要进一步的实证研究予以验证)。
2.对关键识别假设及其潜在威胁的讨论较为全面:由于本文核心变量具有行业和地区两个层面的变异性,从而也就面临两个层面的选择性威胁:(1)行业层面的选择性:劳动力需求下降、国际竞争、其他技术变革对高机器人渗透行业的冲击;(2)通勤区层面的选择性:采用高机器人渗透行业所集中布局的通勤区可能更容易受到其他劳动力市场负面冲击的影响。作者在文中采用多种方式对识别假设给予了间接检验。
3.将数据上的缺陷转换为因果识别策略上的优势:本文在数据上的缺陷在于:无法获取机器人应用程度的微观数据,美国行业层面机器人数据的缺失,由此作者才借助欧洲国家的相同阶段的行业机器人数据作为替代指标,然而,作者论证这种做法实际上能够一定程度缓解了内生性问题(满足外生性),同时,作者还利用了地区机器人供应商的数据,替代性指标能够有效拟合美国国内的实际机器人利用状况(满足相关性)。
4. 对一般均衡效应的讨论十分谨慎:在本文的研究情景下,由溢出效应(或一般均衡效应)导致的STUVA 假定不满足难以真正规避。作者毫不讳言:当地区之间存在贸易时,本地生产的中间品会成为其他地区的中间投入,本地机器人技术进步将降低要素投入成本,带动其他地区的产量扩张,引致劳动力需求提升和工资上升,导致估计系数被高估。为解决这一问题,作者通过对模型参数进行赋值和校准,得出修正后的估计系数。认为即使存在溢出效应,其对就业和工资的影响仍有0.2%和 0.42%。
从文章立意来看,作者使用了新的数据和实证分析手段印证了一个经典话题:自动化对劳动力的替代效应。然而,本文的模型构建以及由此得到的理论命题实际上依赖于一系列假设:静态模型、资本固定,自动化技术外生、无新任务(New task)产生、假定同行业的企业采用同等的技术水平。一方面,当我们把模型进一步扩展到动态、允许有动态的资本积累过程、在自动化技术推广的过程中允许新任务的产生,且在新任务中,传统劳动力具有比较优势(Acemoglu, Restrepo,2018),那么最终的就业效应将取决于挤出效应和岗位创造效应的相对大小。另一方面,若在模型设定中纳入企业的异质性(允许同行业的企业采用不同的技术),从而将企业的自动化决策过程内生化。则可以提出一种竞争性的假说:适应行业技术变革的企业市场份额扩大,劳动需求增加,就业数量增加、退出概率下降;不适应行业技术变革的企业退出行业,释放出劳动力(Aghion, Antonin, 2021),同时由于劳动力市场摩擦的存在、生产任务外包等因素使得这些劳动力没有能够迅速匹配到新创造出来的工作岗位,最终自动化对行业或地区层面的就业和工资水平的影响可能是不确定的。
Abstract
We study the effects of industrial robots on US labor markets. We show theoretically that robots may reduce employment and wages and that their local impacts can be estimated using variation in exposure to robots—defined from industry-level advances in robotics and local industry employment. We estimate robust negative effects of robots on employment and wages across commuting zones. We also show that areas most exposed to robots after 1990 do not exhibit any differential trends before then, and robots’ impact is distinct from other capital and technologies. One more robot per thousand workers reduces the employment-to-population ratio by 0.2 percentage points and wages by 0.42%.
本推文由中国经济转型讨论班(CETW)供稿。
推文作者:江成涛,中国人民大学经济学院 2021级西方经济学博士生
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 