原文信息：

Horrace, W. C., Jung, H., Sanders, S. (2022), “Network Competition and Team Chemistry in the NBA,” Journal of Business & Economic Statistics, 1, 35-49. https://doi.org/10.1080/07350015.2020.1773273.

01

引言

前排预警：原文是一篇非篮球迷看不大懂、篮球迷也很难啃得动的文章。

一套完整的“格林公式”由以下四条构成：

    公式1：你（杜兰特）来之前我们（金州勇士）就是冠军

    公式2：你走之后我们还是冠军（史称闭环公式）

    衍生公式1：来之前你没有冠军

    衍生公式2：走之后你没有冠军

作为让人闻风丧胆的金句，“格林公式”堪称NBA垃圾话历史上的“王冠”。实际上，“格林公式”与体育和商业团队协作中的一个重要议题——化学反应——息息相关。化学反应，被Schrage（2014）奉为业绩分析的圣杯，通常用来刻画普通（角色）成员组成的团队何以超越纸面上无比强大的对手（Brave et al., 2018）。更技术性的定义或许是个人能力和团队业绩因互补协作相互加强。

考虑到“格林公式”已成事实，相对其成立与否，我们更关心公式成立的奥秘。有意思的是，今年正式发表（2020年online）于Journal of Business & Economic Statistics的论文“Network Competition and Team Chemistry in the NBA”，可能恰好揭示了“格林公式”的秘密。作者将NBA比赛解构为球队网络内部的“化学反应”和对战球队间的“网络竞争”。研究发现，球队内部的“化学反应”可以显著提升队内球员的个人表现，而“网络竞争”对个人表现的作用方向不明。由此可见，金州勇士队的口号Strength in Numbers或可为公式正名，而中文“三个臭皮匠顶一个诸葛亮”“团结就是力量”同样鞭辟入里。

言归正传，段子再妙也无法替代科学研究的严谨之美。本文仅堪“网络竞争和化学反应”一文的粗浅介绍，必然无法准确还原原文精巧的模型设定和细致入微的内生性处理。若要窥探此般计量理论文献的要领，请君研读原文。需要说明的是，原文包括引言、模型、仿真、应用和结论五个部分，而本文首先说明格林公式的背景，再依次对原文除仿真之外的部分进行概述。仅关心实证应用的读者也可忽略模型部分。

背景：“格林公式”的来龙去脉

02

在揭秘“格林公式”之前，让我们首先对故事的来龙去脉略作交待，方便热心的非球迷读者熟悉背景。

表针要回拨到2015-2016赛季。金州勇士队在核心三人组史蒂芬·库里、克莱·汤普森、追梦·格林的带领下，乘上一季夺冠之势，创造73胜9负的历史最佳常规赛战绩。在季后赛的西部决赛中，勇士遭遇俄城二少杜兰特和威斯布鲁克的强力阻击，大比分2-3落后，命悬一线（NBA季后赛采取7场4胜制）。接下来，勇士队凭借克莱单场11记三分的神迹赢得第6战，第7场再胜雷霆完成翻盘，击碎了杜兰特的冠军梦。然而，勇士队在总决赛中折戟沉沙，与第二次总冠军失之交臂。

后边儿的情节为人熟知，超级巨星杜兰特在2016年休赛期宣布离开雷霆，身负叛徒恶名毅然加盟勇士，宇宙无敌超级霹雳勇组建完成。在连续夺得2016-2017、2017-2018赛季总冠军后，杜兰特与勇士队的蜜月期渐逝，开始对围绕格林（回顾背景知识：勇士队原有的核心三人组为库里、克莱、格林）展开的进攻体系——球迷戏称为“格林弧顶发牌”——产生不满。矛盾终于爆发。

2018年11月，一场常规赛末节的绝杀回合，杜兰特大喊“把那该死的球给我”“Just pass the dXXn ball”，格林视而不见，勇士遗憾落败。杜兰特对此相当不满，二人公开争论并互致亲切F问候，那句让杜兰特破防的“你来之前我们就是冠军了”横空出世，史称“格林公式”。

故事还没完。2018-2019赛季季后赛，杜兰特拼到重伤，随后离开金州勇士加盟新泽西篮网。2019-2020、2020-2021赛季勇士队战绩一落千丈，舆论开始批评“格林公式”的粗鄙愚蠢导致杜兰特离队，王朝球队因此分崩离析。然而，人生如戏，戏有续集。2022年6月，库里、克莱、格林三人组在没有杜兰特的情况下再次带队夺冠。很快，广大球迷为“格林公式”打了一个补丁——“你走之后我们还是冠军”，史称“格林公式闭环”。鉴于杜兰特在来前和走后均未能染指冠军，“格林公式”又开发出前文所述衍生版本。

公允而言，杜兰特拥有历史级别的个人得分能力，也为奠定勇士王朝做出了卓越贡献，只是不巧遭遇史诗级垃圾话罢了（考虑到近期传出杜兰特申请离开篮网的新闻，“格式公式”或许还有新篇章）。严肃而论，格林公式无非意是说勇士体系的作用远胜于某个超级巨星，或者说化学反应的重要性。

03 

定位：本文估计化学反应的情境

原文是在以下特定的情境下刻画并估计化学反应：一个大的互动网络由多个团队构成（r = 1, ... , R），每个团队包括一定数量的个体成员（nr），个体成员在与团队内部同伴（peers）互动的同时，也以团队间竞争的方式与其他团队的成员（non-peers）进行互动。一方面，化学反应指向的绩效是单维的（理论上也可以是多维的）；另一方面，团队间的竞争采取捉对厮杀（head to head）的形式而非同时性的多队大混战（在模型设定阶段允许大混战，而在基于NBA比赛进行实证研究时限定为捉对厮杀）。

团队竞争中一个不容忽视的要素是每个团队内部往往存在一个中央计划者，比如球队教练。计划者的选择会导致内生性问题，比如教练的排兵布阵显然会影响战绩。作者主要通过两种方法克服选择性偏差：一是标准多项式logit模型（standard multinomial logit - MNL），二是机器学习中的随机森林算法（random forest - RF）。特别的，由于仅有教练在每期的行动都能被观察到，并且教练将决定哪些成员能在某个时点上场，因而被观察到并参与竞争（同样想象教练决定哪些球员上场），本文设定的团队互动是跨期时变（time-varying）的（t = 1, ... , T），符合重复横截面（repeated cross-sections）而非面板数据（not panel）的结构。足够大的T使得我们能够得到同伴效应的准极大似然（quasi-maximum-likelihood，QML）一致估计量。进一步研究表明，在nr较小（篮球比赛中每队场上球员为5人，nr=5）的情况下，自举（bootstrap）误差修正方法也可以在有限样本中得到较为理想的估计量。

模型：产出函数与估计策略

04

4.1产出函数

存在R个团队/网络，每个团队（r = 1, ... , R）由nr个成员/同伴组成，因此个体成员总数为。个体成员在团队内部协作同时与其他团队成员展开竞争。第r个团队的产出函数为：

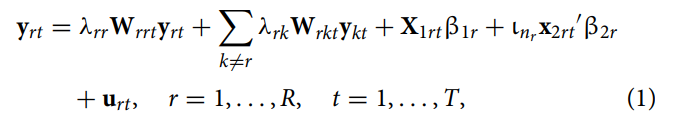
这里yrt表示第r个团队nr×1的产出向量，X1rt为nr×p1的外生的投入矩阵，该矩阵随不同个体成员（i = 1, ... , nr）和时期t（个体层面）变动，ιnr为nr×1的单位向量，x2rt是p2×1的外生的投入向量，随t变动（团队层面），urt为nr×1误差项向量。Wrrt表示第r个团队内部互动的nr×nr权重矩阵，Wrkt表示（k ≠ r）第k个团队对第r个团队的nr×nk效应矩阵。由此假设λrr为第r个团队内部的同伴效应均值，λrk表示r团队与k团队进行网络间交互时竞争效应的均值。β1r和 β2r分别表示r团队投入要素的系数向量。已有文献假设λrk = 0（k ≠ r），而本文不仅允许网络内（with-in network）效应的存在，还考虑了网络间（cross-network）效应。

进一步，每个团队r存在一个计划者，在时期t从人员储备池中选取nr个成员组建团队，团队内的同伴通过共担使命并与其他团队的成员竞争创造产出yrt。显然，计划者的策略性选择对计量模型存在影响。仅当i在t期被计划者选中进入团队r时，我们才能观测到i的产出yirt，可见这种数据结构属于重复截面而非面板（不同t的截面组成未必一致），由此也很难通过控制团队层面的固定效应缓解Manski（1993）所言关联效应（correlated effect）。

不失一般性，我们假设所有的计划者面临同样数量的人员储备n0＞nr，令dirt＝1表示i在t期被选入r，否则dirt＝0。由此计划者的决策为Dt = (d1t, ... , dRt) ， drt = (, ... , )′。所谓关联效应即E(urt|Dt) ≠ 0，Dt显然与公式（1）等号右侧的变量相关。最后，作者参考不完全信息静态博弈的多重均衡为计划者的决策建模。为便于分析，首先假设决策者对r团队中所有同伴的影响一致，此时关联效应简化为时变（time-varying）的团队/网络固定效应。也就是说，

进一步仍需要满足以下3个假设正则条件：

准极大似然估计（quasi-maximum-likelihood，QML）的一致性需要满足nr趋于无穷大，但假设1中跨t期的独立性可以得到一致的准极大似然估计量。进一步由假设1可知，当固定数量的R中跨期独立且nrT趋于无穷大时，QML估计量满足一致性。假设2中，参数空间紧集能够确保ML估计的一致性和较为理想的的渐近性。在假设2的充分条件得以满足时，假设3成立，假设3使空间依赖问题能够被处理。

产出函数的QML估计由以下公式（3）、公式（4）、公式（5）给出，进一步的假设4和假设5同样见下图：

4.2策略互动引致的偏误

偏误估计部分细节拉满、公式繁多，建议感兴趣的读者细读原文，此处不再展开。

05 

基于NBA比赛的应用

5.1实证模型和变量

实证检验部分将上述模型应用于2015-16赛季NBA常规赛的30支球队。作者将来自BigDataBall.com的原始数据整理为球员-时段/时期（player-period）结构，所谓时期指相同10个球员同时在场的不间断时段。以基于球员个人统计数据的“致胜产出”指标作为产出变量（Wins Produced）。（注：NBA开发了一系列用于衡量球员水平的统计指标，比如真实正负值Real Plus Minus。类似的指标也常用于MLB美职棒，参见电影《点球成金Moneyball》）。NBA常规赛季总共举行1230场比赛（30支球队各有41场主场比赛），形成大约1,122,040个原始观测点。教练有15个球员可供调配以组成5人（nr＝5）的场上阵容（暂不考虑伤病问题），剔除时长小于30秒（回顾前文关于period的定义）和加时赛时段，最终剩下约833,000个观测点。

5.1.1产出函数

鉴于NBA比赛采取一对一捉对厮杀模式，此处可就前述模型的简化版本加以应用，即在每个时段只有一个同伴网络和一个对手网络。在这种情况下，比赛g中时段t下球队r和球队k的产出函数由下式给出：

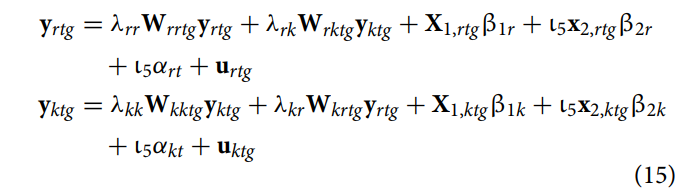
Wrrtg和Wkktg表示5×5阶对角为0且行规范化的矩阵，用于捕捉球队内的同伴效应。类似的Wrktg和Wkrtg分别表示球队间互动矩阵。X1,rtg和X1,ktg分别表示因球员而异（个体层面）的外生变量矩阵。x2,rtg和x2,ktg分别表示球队层面的外生变量，可在组内变化中消掉，但其系数将用于估计教练选择偏差。urtg和uktg表示分别服从iid (0, σ2r ) 和 iid (0, σ2k )分布的误差项。

5.1.2选择方程（决定状态Zgrt的函数）

为确保公式（15）能够被识别（满足假设4）并尽量逼近教练排兵布阵的实际情况，文章假设教练在进攻回合中使用错位策略（mismatches，想象姚明背打郭敬明或艾佛森单打姚明）。因此作者以当期场上后卫数（Nguardrt）作为选择方程的被解释变量（下文将说明原文语境下的球员只分为后卫和前锋两种类型），即，MNL模型中球队r在时段t的行动集为，表示当期场上后卫数量。考虑到教练的决策很可能是非线性的，作者还使用RF方法进行了估计。

5.1.3网络

在错位策略的基础上，作者进一步以球员是否属于同一类型来刻画网络效应的权重。所谓类型即球员的位置：后卫（Guard）或前锋（Forward）（为简化分析，这里的前锋包括中锋）。也就是说，出于识别的需要，假设每个球员仅与同队内同类型球员和对手队内同类型球员产生交互。比如，若球队r的场上阵容为[F,F,G,F,G]'，球队k为[G,F,F,G,G]'，则网络权重矩阵如下所示：

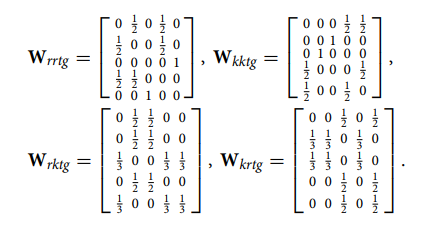
5.1.4变量

作者基于“致胜产出”指标（Wins Produced）衡量产出并给出如下计量模型：

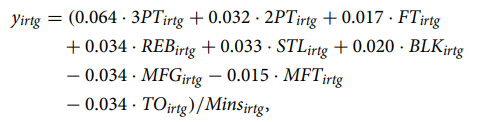
注意3PT、2PT、FT分别表示3分、2分和罚球（1分）命中。REB表示篮板（Rebounds）、STL（Steals）表示抢断、BLK（Blocks）表示盖帽、MFG表示错失的投篮（Missed Field Goals）、MFT（missed free throws）表示错失的罚球、TO（turnovers）表示失误、Mins表示球员i的出场时间（minutes played by player i of team r in period t of game g）。被解释变量使用Wins produced per minute，基于球员个体层面变量衡量某球员对球队胜利的边际贡献。

5.2实证结果

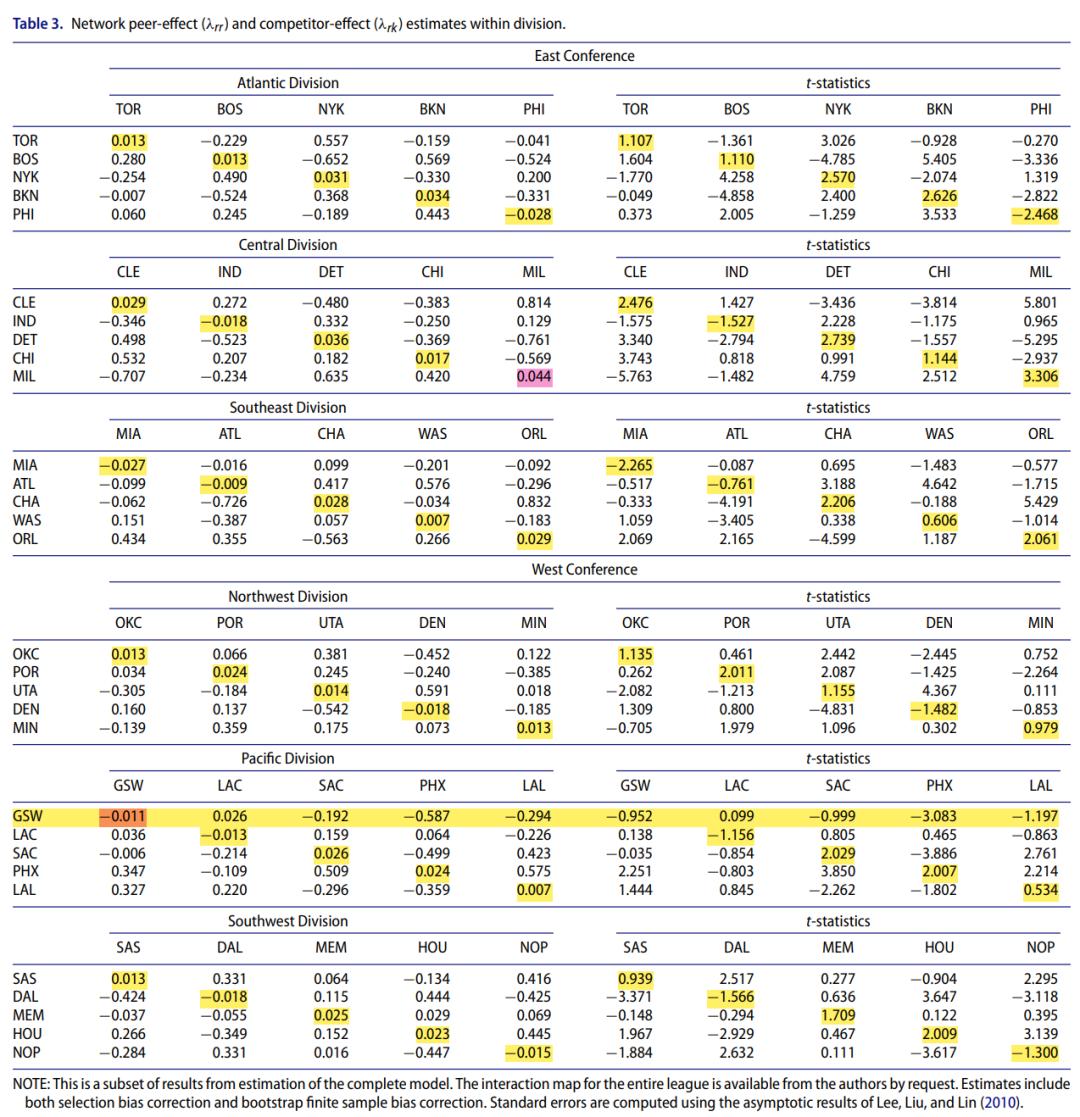
如下图所示，作者基于东西部联盟的几大分赛区（赛区设置主要是出于地理临近的考量，同一赛区内球队一个赛季内要交锋4次，比不同分区对战更多）报告了相应的结构方程估计系数。图的左侧为交互系数，右侧是相应的t值。系数接近＋1和－1分别表示好的和坏的交互效应。我们关心的网络内部化学反应由图左侧对角线上的系数表示。

不难发现，代表良性化学反应的正向的系数大多在统计上显著，而负向系数几乎都不显著。因此可以说化学反应的积极影响得到了验证。在以分区估计的化学反应中，密尔沃基雄鹿队表现最好，相应系数达到30个球队中最高且显著的0.044，这或许预示着雄鹿队此后的夺冠？而唯一一个负向显著的网络内系数来自迈阿密热火，意味着2015-16赛季热火队的化学反应可谓相当糟糕。

回到笔者关心的金州勇士队，尴尬的是，表征勇士化学反应的系数为负，尽管并不显著。作者给出的解释可供参考：本文的化学反应是在策略、能力、对位等限制条件下进行的估计，并不能反映球队的实力。一个天才射手即使出手选择糟糕也能投进（比如库里和克莱），一支充满天赋的球队化学反应很差也能赢球。在笔者看来，文中所示勇士队化学反应欠佳的原因可能有三个：1、将网络内外互动限定在同类型球员带来的局限性，要知道勇士三人组库汤追各自的位置并不一致，而不同位置球员的化学反应本文无法考察。2、将效应估计限定在分赛区内忽视了勇士队与分区外球队对战的情况（原文线上补充材料提供了更全面的估计结果）。3、考察时间限定在2015-16赛季常规赛可能导致偏差。

结论

06

基于对空间自回归模型（SAR）的拓展，作者们开发出一个网络竞争模型，该模型可以同时估计网络（团队）内成员的同伴效应和网络间成员的竞争效应。本文为刻画市场互动提供了一幅更加完整的图景，这或许有助于我们理解并预测外生冲击对某个单一网络的影响如何扩散到整个市场。作者将该模型应用于2015-16赛季NBA常规赛的30支球队，发现正向的队内化学反应（同伴效应）和可正可负的竞争效应。这即是说，拥有良性化学反应的球队能够提升或削弱对手的表现。相对于已有文献中其他联立SAR模型，该模型多少有一定的局限性，因此未来的工作应该致力于探索更加一般化的基本模型。比如，在产出函数中引入外生网络效应（exogenous network effects , e.g., WrrtX1t），也应该考虑误差项中时序和横截面的相关性（即放松假设1）。从网络内部同伴间的视角考察选择偏误同样富有价值（放松假设5）。就我们针对NBA的应用而言，开发一个基于传球和分享球权的同伴效应加权方案将会十分有趣。

此外，关于化学反应的研究不仅涉及职业棒球联盟MLB（Brave et al., 2018）等其他团队竞技运动，还已经扩展到学术合作的成效分析（Son et al., 2022）。感兴趣的读者不妨深耕。

延伸阅读：

Schrage, M. (2014), “Team Chemistry Is the New Holy Grail of Performance Analytics,” Boston, MA: Harvard Business School Publishing. https://hbr.org/2014/03/team-chemistry-is-the-new-holy-grail-of-performance-analytics.

Brave, S. A., Butters, R. A., Roberts, K. A. (2018), “In Search of the Holy Grail: Team Chemistry and Where to Find It,” Working Paper. https://www.chicagofed.org/~/media/others/people/research-resources/brave/brave-working-paper-2017-in-search-of-the-holy-grail-team-chemistry-and-where-to-find-it-pdf.pdf.

Son, G., Yun J., Jeong, H. (2022), “Quantifying Team Chemistry in Scientific Collaboration,” arXiv, https://doi.org/10.48550/arXiv.2202.07252.

推文作者：张亦达

邮箱：zxy_morgan@163.com

Abstract 

We consider a heterogeneous social interaction model where agents interact with peers within their own network but also interact with agents across other (non-peer) networks. To address potential endogeneity in the networks, we assume that each network has a central planner who makes strategic network decisions based on observable and unobservable characteristics of the peers in her charge. The model forms a simultaneous equation system that can be estimated by quasi-maximum likelihood. We apply a restricted version of our model to data on National Basketball Association games, where agents are players, networks are individual teams organized by coaches, and competition is head-to-head. That is, at any time a player only interacts with two networks: their team and the opposing team. We find significant positive within-team peer-effects and both negative and positive opposing-team competitor-effects in NBA games. The former are interpretable as “team chemistries” which enhance the individual performances of players on the same team. The latter are interpretable as “team rivalries,” which can either enhance or diminish the individual performance of opposing players.

声明：推文仅代表文章原作者观点，以及推文作者的评论观点，并不代表香樟经济学术圈公众号平台的观点。