推文人 | 王彦锋 

参考文章：

[1] Martellini, Lionel and Volker Ziemann. Improved estimates of higher-order comoments and implications for portfolio selection. The Review of Financial Studies,2009,23(4),1467-1502.

[2] Kris Boudt, Dries Cornilly and Tim Verdonck. A Coskewness Shrinkage Approach for Estimating the Skewness of Linear Combinations of Random Variables，Journal of Financial Econometrics,2018,1-23.

 

1.引言

 

随着金融市场的发展，过去经典投资组合理论已经不再适合当前的金融市场。相比于过去，当前金融市场主要变化之一在于数据的收集方面。如今，高频率的数据收集变得越来越方便。众多学者发现，低频数据（像季度数据、年度数据等）的收益率的分布往往服从正态分布，然而高频率的数据（日数据、小时、分等）不再服从正态分布。高频率的数据相比于低频数据往往包含着更多的信息。投资者利用高频数据信息来构建投资组合往往会给他们带来更多的收益以及更小的风险。高频率的收益率数据最典型的特征之一是其分布往往具有尖峰厚尾的特征。这些特征可以通过变量的高阶矩特征来反映出来。当前，越来越多的学者开始将高阶矩加入到传统的投资组合模型中，并利用高阶矩信息构建投资组合。然而利用高阶矩信息将面临一个直接的问题即高阶矩估计问题。相比于均值（一阶矩），方差-协方差矩阵（二阶矩），更高阶矩（三阶矩和四阶矩）拥有更多的参数。举个例子来说，如果一个投资者想在20种股票中做投资组合，在加入高阶矩信息之后，利用传统的样本估计来估计参数的话，待估参数将达到10605个。因此，为了保证估计精度，需要的样本量往往非常巨大。在样本量较少的情况下，往往会造成较大的估计误差。因此，学者们在估计高阶矩时，往往对高阶矩施加结构上的约束（比如假设高阶矩中某些参数为0等）从而减少待估参数。然而施加结构上的约束往往会造成设定误差。因此，为了在设定误差与估计误差中找到一个平衡，压缩估计的方法被一些学者提出来。

 

2.压缩估计的原理及方法

 

Martellini和Ziemann(2010)将此方法扩展到高阶矩的估计上。即将公式（1）中的结构化估计的方差协方差矩阵以及样本估计的方差协方差矩阵换成结构化估计的高阶矩以及样本估计的高阶矩。在Martellini和Ziemann(2010)这篇文章中，对于高阶矩结构化的估计，作者给出了两种方法：一种是常相关估计，另一种是单因子模型估计。这两种估计方法都极大地减少了高阶矩中待估参数的个数，减少了样本估计误差，但也在一定程度上增加了设定误差的风险。作者将结构化的高阶矩估计与样本估计进行压缩得到了高阶矩的压缩估计方法并将其应用到投资组合中。Kris等（2018）给出了高阶矩（三阶矩）的另一种结构化的估计方法，采用与Martellini和Ziemann(2010)相同的思路得到了高阶矩的压缩估计并将其应用到投资组合中。对比两篇文章，不同之处除了在于使用不同的结构化方法来估计高阶矩外，还在于Martellini和Ziemann(2010)中所估计的最优压缩强度并非具有一致性，而Kris等（2018）给出了最优压缩估计强度的一致估计，此外，Martellini和Ziemann(2010)这篇文章只考虑了单目标压缩的方法，即一次压缩只考虑一种结构化的估计与样本估计；而Kris等（2018）这篇文章还采用多目标压缩，即同时考虑多种结构化的估计与样本估计进行压缩。

 

3.压缩估计的估计结果

 

在此给出Martellini和Ziemann(2010)以及Kris等（2018）两篇文章模拟结果。

 

 

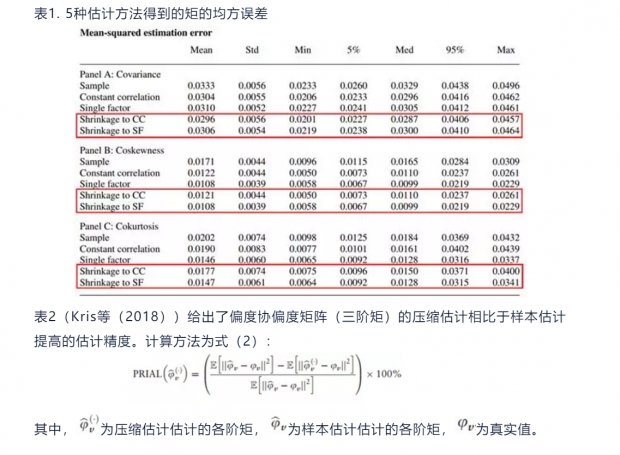
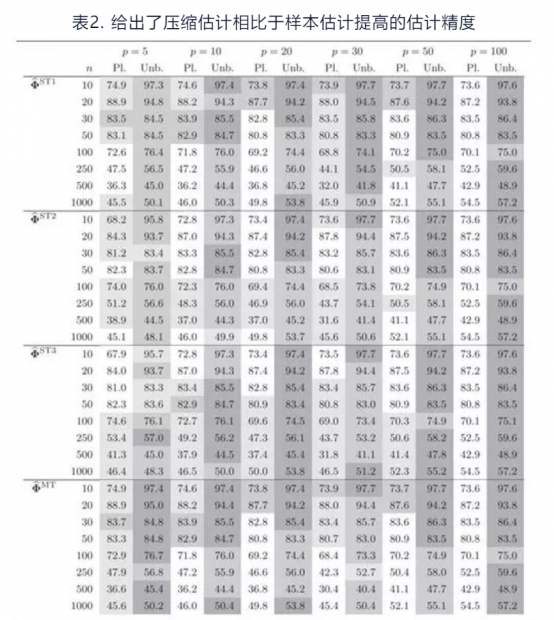
从上式可以看出，PRIAL值越大，说明压缩估计的方法相比于样本估计效果提高的更大。表2中的p表示资产个数，n表示样本量，ST1、ST2、ST3分别表示3种不同的结构估计方法。MT表示将三种结构估计的高阶矩与样本估计进行多目标压缩。Pl表示采用有偏的估计，Unb表示采用无偏的估计。

 

从表2中我们发现压缩估计方法对于偏度协偏度矩阵的估计要明显优于样本估计方法。

 

 

4 .结语

 

压缩估计方法的主要思想在于通过某种组合方式将不同的估计方法估计的矩进行组合。在以上两篇文章中，他们都是运用线性组合的方式将结构化的估计方法与样本估计方法进行压缩。结构化的估计势必带来一定的设定误差，而样本估计方法也会在一定程度上带来估计误差，因此为了在设定误差与估计误差之间找到一个均衡点，压缩估计不失为一种方法。