推文人 | 文惠

原文信息：Guillaume R. Fréchette, Alessandro Lizzeri, and Tobias Salz,“Frictions in a Competitive, Regulated Market: Evidence from Taxis”, American Economic Review 2019, 109(8): 2954-2992.

图片来源：Guillaume R. Fréchette, Alessandro Lizzeri, and Tobias Salz,“Frictions in a Competitive, Regulated Market: Evidence from Taxis”, American Economic Review 2019, 109(8): 2954-2992

 

 

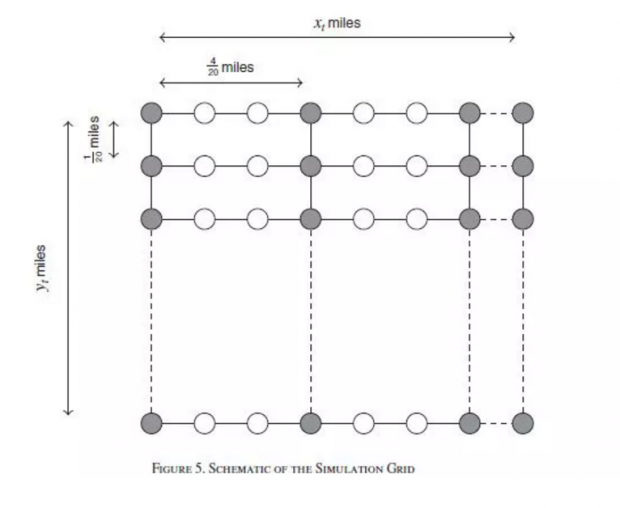
——基于纽约市出租车市场的模拟分析

 

引言

 

近年来，随着移动互联网、智能手机和GPS定位技术的发展，网约车平台快速兴起和普及，已经深度改变了出租车市场的打车方式。截至2016年12月，我国网约车用户约4亿人，网约车出行方式在一线城市的渗透率达到40%。出租车市场虽然具有很多完全竞争市场的特征，比如有很多家出租车公司、每家公司独立地做出供给决策、劳动力和资本的供给都比较充足，但是在打车过程中出租车和乘客“匹配摩擦”一直是限制市场效率的重要因素之一。今天推送的这篇文章提出了一个出租车市场的动态均衡模型。本文的新颖之处在于使用模拟算法构造了出租车与乘客之间的匹配函数，提高了结构模型对于数据的拟合度，并通过结构模型以纽约市出租车市场为例模拟分析了打车平台的匹配技术与平台竞争对市场效率的影响。

 

背景及数据

 

本文使用了纽约市2011年10月1日至11月22日和2012年8月1日至9月30日的4个月的出租车市场数据进行分析。在这期间，挂出租车牌照的黄色出租车为出租车市场中的主体，Uber当时在纽约市尚不普及。其中，大约40%的出租车牌照由个体经营者所拥有，60%由70家出租车公司所拥有。按照纽约市出租车牌照的管理规定，个体经营者每年至少驾驶210个班次才能保有牌照。出租车公司按日或星期将出租车牌照租给司机。出租车公司的出租车必须每天至少出车两个9小时以上的班次。

 

本文的数据来源于纽约市出租车乘客提升项目（Taxicab Passenger Enhancements Project）。该项目对每一次出租车行程都进行了详细的记录。在样本的时间区间，共观测到了13520个有活动记录的出租车牌照和37406名不同的司机。通过初步观察一周7天每天中每小时的活动出租车数量，作者发现周一至周四具有相似的变化规律，而周五至周日的变化规律则差异较大，因此作者将分析集中在每周周一至周四4天时间。由于90%以上的出租车行程起始于曼哈顿区，作者又进一步将分析范围集中在从曼哈顿出发的出租车行程。

 

模型与估计

 

由于纽约市出租车市场实行固定价格体制，出租车市场上主要决定市场出清的变量是乘客打车的等候时间和出租车寻找乘客的寻找时间。

 

A. 需求模型

 

打车需求Dt为所有决定打车的乘客数量，是等候时间Wt的函数。这些乘客中一部分匹配成功打到了车，另一部分由于等候时间过长（作者假定超过20分钟）而放弃打车，即未匹配成功。估计打车需求模型面临两个困难。第一，现实中虽然可以观察到匹配成功的乘客数量，但是未匹配成功的乘客数量和每位乘客的等候时间都观察不到。第二，平均等候时间和打车需求还具有同时性。

 

作者解决这一问题的新思路是通过可以观察到的出租车寻找乘客的寻找时间St来推测乘客的等候时间Wt。这个思路的提出是基于一个直观的观察：假设路上车流速度等相关因素都相似，对于同样数量的寻找乘客的出租车，更长的寻找时间意味着较少的乘客在等候出租车。更确切地说，作者将这一联系概括为一个匹配映射：

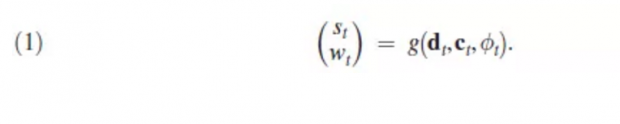
其中, g()是一个匹配映射，dt是等候出租车的乘客数量，ct是寻找乘客的出租车数量，t是随时间改变的外生变量，包括车流速度和平均行程距离, St是出租车寻找乘客的时间，Wt是乘客等候出租车的时间。如果可以推测出匹配映射g()，那么给定乘客数量（dt）、出租车数量（ct）、车流速度和平均行程距离，就可以推测出等候时间Wt。

 

作者根据曼哈顿区的地理特征，将映射过程简化为了在一个等距离网格上的匹配过程。然后，作者分别仿真模拟估计了出租车巡游模式下的匹配映射g()。曼哈顿区的地图（Figure 20）和作者简化的网格示意图（Figure 5）如下。

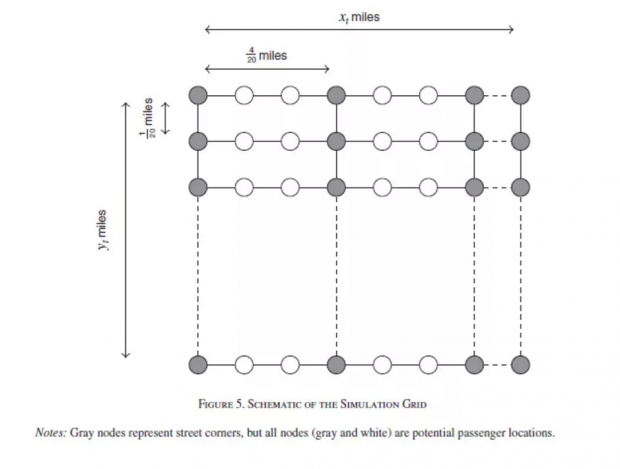
在仿真模拟出匹配映射g()之后，基于数据中观察到的出租车的寻找时间、出租车数量、车流速度和行程距离，作者使用模拟匹配映射g()推测出了等候出租车的乘客数量，并进而估计出等候时间。在得到推测出的这两个关键变量的数值之后，作者对需求函数做了进一步的估计。需求函数的形式如下：

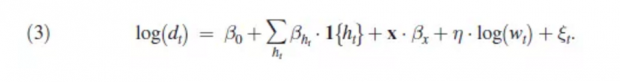
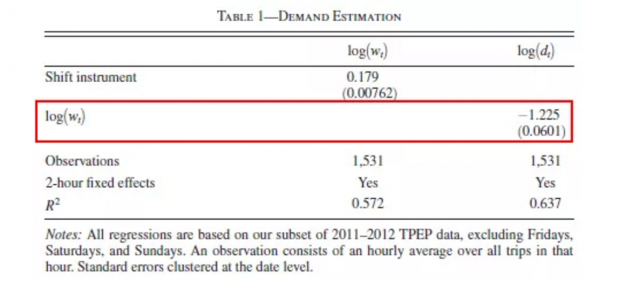
其中，ht是代表一天中24个小时的虚拟变量。为了解决Wt的内生性问题，作者使用了出租车供给侧的司机白班和夜班的换班时间作为工具变量。由于出租车牌照的出租价格受上限管控，出租车公司的换班时间的最优选择是使白班和夜班给于司机带来的收益趋于一致。需求估计结果见表1。

B. 供给模型

 

作者在建立供给模型时细致地考虑了司机每个小时的供给决策，因为司机每个小时都可以决定自己是否进入或者退出出租车市场。供给模型的构建思路是将基于状态变量的价值函数引入司机的效用函数，假设成本函数为劳动力供给的凸函数，求解出司机在效用最大化下的最优进入概率和退出概率。

 

C.竞争均衡

 

基于上述结构模型，作者定义了出租车市场上的竞争均衡为出租车的平均每小时内的寻找时间St，乘客的等候时间Wt，出租车数量Ct，乘客数量Dt（包括已经打到车和正在等候的乘客），司机每小时的收入πt，且满足：

 

(1). 乘客数量Dt来自等候时间为Wt时的需求函数；

 

(2). 寻找时间St和等候时间Wt来自乘客数量为Dt、出租车数量为Ct时的匹配映射g()；

 

(3). 出租车数量Ct基于司机最优进入概率和退出概率；

 

(4). 司机每小时的收入基于平均每小时内的寻找时间St。

 

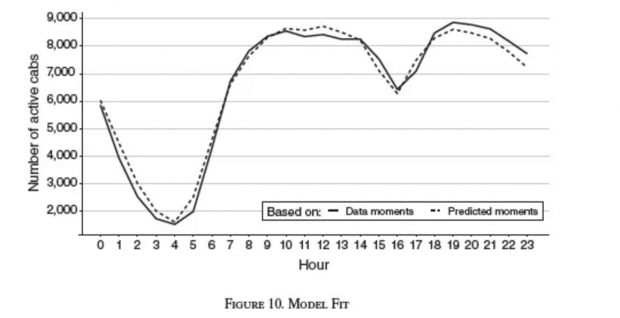
图10显示该竞争均衡下的供给预测与实际数据的拟合度相当高。

 

【模拟分析】

 

基于上述估计出来的结构模型，作者分析了引入网约车平台和平台竞争对于市场效率的影响。作者进一步使用仿真模拟网约车平台的匹配技术的方法建立了网约车平台的匹配映射g()，以用于模拟分析。然后，作者首先模拟了市场完全使用网约车平台的结果，并和之前仅使用巡游模式的情况进行了对比，结果见图13。

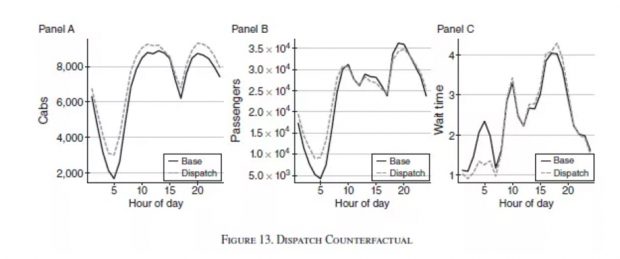
模拟分析数据显示，市场上活跃的出租车数量增加了9.57%，出租车的寻找时间下降了8.65%，需求增加了4.87%，等候时间下降了1.94%，消费者剩余增加了6.89%，而打车次数增加了12.24%。司机和乘客都因为引入了网约车平台而获得了好处。

 

由于网约车平台在引入阶段往往不能覆盖全部市场，作者考虑了市场上的出租车牌照一半服务于网约车平台，一半采用巡游模式的情况，并假设乘客被外生决定仅使用其中一种打车模式。在这种情况下，消费者剩余和司机每小时的收入比市场上仅使用巡游模式的时候都低。作者指出这是由于这样的市场分割降低了市场厚度，带来了负效应。当作者放宽假设，允许乘客自由选择使用网约车平台或在路边招手打车时，乘客的福利效应得到改善，但是司机的境况会变得更糟。此外，作者又考虑了两个网约车平台分割市场进行竞争的情况。这种情况下，消费者的福利效应、司机收入比市场上仅使用巡游模式的时候都低。

 

结论

 

这篇文章将模拟算法引入了结构模型，为求解结构模型带来了新思路。作者以纽约市出租车市场为例初步模拟分析了网约车平台的匹配技术与平台竞争对市场效率的影响。作者发现，虽然网约车平台的匹配技术显著减少了匹配摩擦，改进了市场效率，但是平台的引入和竞争也可能引起市场厚度下降而带来一定的负效应。

 

Abstract

 

This paper presents a dynamic equilibrium model of a taxi market. The model is estimated using data from New York City yellow cabs. Two salient features by which most taxi markets deviate from the efficient market ideal are, first, matching frictions created by the need for both market sides to physically search for trading partners, and second, regulatory limitations to entry. To assess the importance of these features, we use the model to simulate the effect of changes in entry, alternative matching technologies, and different market density. We use the geographical features of the matching process to back out unobserved demand through a matching simulation. The matching function exhibits increasing returns to scale, which is important to understand the impact of changes in this market and has welfare implications. For instance, although alternative dispatch platforms can be more efficient than street-hailing, platform competition is harmful because it reduces effective density. (JEL C78, L51, L84, L92, L98, R48)