推文人 | 杨柳 

原文信息：Steven Berry, James Levinsohn and Ariel Pakes (1995). Automobile Prices in Market Equilibrium. Econometrica 63(4), 841-890.

 

一、引言

 

BLP模型是实证产业组织（Empirical Industrial Organization）中的奠基性论文。后续很多理论模型都是基于BLP在1995年的开创性框架。一般来说，如果研究者关心某个差异化产品市场中的均衡问题，BLP模型都是不可缺少的研究工具。所谓差异化产品（Differentiated products）市场，即微观经济学中讨论的垄断竞争（Monopolistic competition）市场，每个企业各自生产有差异化的某类产品，不同企业生产的产品之间存在一定的替代性，企业在各自的细分市场上采用利润最大化定价，同时考虑其他企业的定价方案。汽车市场是典型的差异化产品市场。不同品牌、不同型号的汽车具有不同的产品参数，但是因为同属汽车这一大类产品，相互之间又并不是完全不可替代的。BLP模型能够帮助研究者评价某一些公共政策，比如对新能源汽车的购买补贴，及其对汽车市场的影响（包括对消费者福利、市场成交价格、企业利润、各种汽车的市场份额等）。由于这些政策可能并未在现实中执行，研究者无法使用标准的基于反事实（Counterfactual）的reduced-form estimation（比如DID等）方法，此时，BLP模型可能是唯一的选择。

 

二、主要内容

 

1995年的这篇论文假设研究者能够观测整个新车市场的交易数据，即每一年每一款车型的交易量和成交价格（可能包括很多年），以及每一款车型的特征参数（如重量、排量、自动/手动、几座等）。另外，BLP还假设研究者能够观测整个国家每个家庭的收入情况（大部分来自统计局的普查数据）。BLP在2004年发表于JPE上的论文更是假设研究者能够观测到购买了不同车型的家庭特征（包括收入、年龄、家庭规模、职业、受教育水平）等微观数据，从而使得最终的估计量更为精确。

 

BLP模型分为两个部分，第一部分研究消费者的效用最大化问题，第二部分研究生产者的利润最大化问题。在第一部分中，最核心的问题是如何使得估计出来的市场需求函数具有现实中典型的替代类型（Substitution pattern），即特征相似的车型替代弹性较高、收入较高的家庭对不同车型的替代弹性较低。传统上基于logit模型的离散选择模型不能导出具有上述特征的市场函数。BLP因此假设消费者i对车型j的效用函数为如下形式

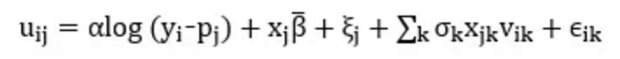
其中，x=(x_1,x_2,…,x_K)是车型j的K个可观测特征，β ̅+σ_k v_ik代表特征k对消费者i的边际效用，因为v_ik含有下标i，所有特征k对不同消费者带来的边际效用是不一样的，假设v_ik服从独立同分布的标准正态，则σ_k可理解为边际效用在人际之间的标准差。p是车型j的成交价格，ξ是车型j的不可观测特征（比如质量），y是消费者i的收入，ϵ是服从type-I极值分布的随机扰动项。为了分析的方便，BLP假设ϵ是独立同分布的，并且与（x,p, ξ）独立。ξ与价格p之间可能存在一定的相关性（质量越高的车通常卖得越贵）。基于type-I极值分布的特性，消费者i选择车型j的概率具有显示解。

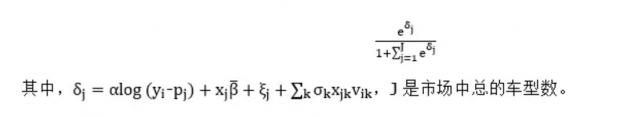
研究者不能观察到所有消费者的特征(y_i ,v_i1,v_i2,…,v_iK)，但是我们知道这些特征的分布：y_i的分布可从普查数据中估计（BLP假设y_i服从对数正态分布，一般地，y_i的分布可使用非参数方法估计获得），v_ik假设服从独立同分布的标准正态，BLP还假设y_i和(v_i1,v_i2,…,v_iK)也是独立的。这样，通过对市场中所有消费者进行加总（积分），就可以获得车型j的市场份额（Market share），

另一方面，车型j的市场份额可由交易数据直接获得。假设经济中总的家庭数为N，如果每个家庭一年最多购买一辆车，那么车型j的市场份额s_j为q_j/N，其中，q_j为车型j的成交量。综合两方面，可得如下等式：

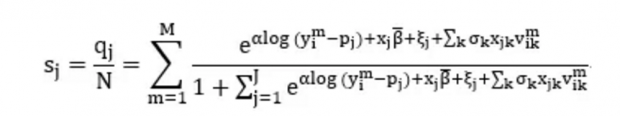
记上式中所有未知参数组成的向量为θ=(α,β ̅,σ_1,σ_2,…,σ_K)，则可求解不可观测特征ξ_j 。

 

ξ_j=g_j (s_1,s_2,…,s_J,p,x,θ)

 

求解ξ_j的过程相对比较复杂，需要解J个非线性方程组，BLP证明这个方程组存在唯一解，通过构造一个压缩映射（Contraction mapping），这个唯一解就是压缩映射的不动点（Fixed point），任意初始点都将收敛到上述唯一解。

 

BLP在第二部分考虑了生产每个车型企业的利润最大化问题。给定市场上总的家庭数N和车型j的market share，厂商j（假设规模报酬不变）的利润可表示为

 

(p_j-mc_j)Ns_j (p,x,ξ,θ,P_0 )

 

其中，mc_j=e^(w_j γ+ω_j )为厂商的边际成本，w_j为影响边际成本的可观测特征，ω_j为影响边际成本的不可观测特征。厂商j选择价格p_j实现利润最大化，其一阶条件为

 

 

 

ω_j=h_j (s_1,s_2,…,s_J,p,x,θ)。

 

BLP假设所有车型的可观测特征(x,w)与车型j的不可观测特征(ξ_j,ω_j)不相关，那么可以得到如下矩条件

 

基于这个矩条件，可以采用广义矩估计（GMM）得到未知参数与θ的估计量，只要距条件的个数大于（过度识别）等于（恰好识别）未知参数θ的个数即可。为了得到估计的渐进有效性，BLP还讨论了最优工具变量和最优随机模拟的内容。详细的分析过程，请参阅原文。

 

三、结论

 

BLP使用这一分析框架估计了美国1971-1990年汽车市场的均衡，得到了不同型号汽车的需求价格弹性和交叉价格弹性，也得到了不同车型的mark-up。由于估计的参数θ描述的是消费者的效用和企业的技术参数，属于与政策没有直接关系的原始参数（primitive parameter），因此可以使用这一模型研究政策实施后汽车市场可能发生的变化（如果参数不是primitive，那么很可能会受政策影响，那么该模型就不可能用来评估政策效应，这就是著名的Lucas critique），从而做相应的比较静态分析。

 

Abstract

 

This paper develops techniques for empirically analyzing demand and supply in differentiated products markets and then applies these techniques to analyze equilibrium in the U.S. automobile industry. Our primary goal is to present a framework which enables one to obtain estimates of demand and cost parameters for a class of oligopolistic differentiated products markets. These estimates can be obtained using only widely available product-level and aggregate consumer-level data, and they are consistent with a structural model of equilibrium in an oligopolistic industry. When we apply the techniques developed here to the U.S. automobile market, we obtain cost and demand parameters for (essentially) all models marketed over a twenty.